Renderman (Partie 1)
Interface de description de scènes 3-D introduite par PIXAR pour être utilisée en synthèse d'images.
Permet la modélisation d'objets, de scènes, de lumières et de caméras.
Permet la modélisation de l'apparence de ces objets.
Utilisé au cinéma dans le domaine des films d'animation (Tin Toy, Toy Storie, 1001 Pattes) et des effets spéciaux (Abyss).
Fonctionnalités
Utilisation d'un petit nombre de primitives graphiques
Modélisation hiérarchique
Constructive Solid Geometry
Géométrie hiérarchique
Modèle de caméra
Attributs d'éclairage
Extensibilité
Syntaxe
Bibliothèque C classique
Toutes les fonctions commencent par Ri.
Exemple 1
/* Copyright Pixar 1989 */
#include <ri.h>
RtPoint Sq[4] =
{{ .5, .5,.5},{ .5,-.5,.5},
{-.5,-.5,.5},{-.5, .5,.5}};
void main(void) {
RiBegin(RI_NULL);
RiWorldBegin();
RiSurface("constant",RI_NULL);
RiPolygon((RtInt) 4,RI_P,
(RtPointer) Sq,RI_NULL);
RiWorldEnd();
RiEnd();
}
- RiBegin(): Initialisation de l'environnement
RiEnd(): Fermeture de l'environnement
RiWorldBegin(): Début de la description d'une scène
RiWorldEnd(): Fin de la description d'une scène
RiSurface(): Type de rendu des couleurs
RiPolygon(): Définition d'un polygone

Deux types de fonctions :
nombre de paramètres constant
nombre de paramètres variable :
La liste variable est composée d'une suite de couples (Token,param). Token indique le type de param à la fonction. Un RI_NULL marque la fin de la liste de paramètres.
Exemple
RiPolygon((RtInt) 4,RI_P,
(RtPointer) Square,
RI_NULL);
Les fonctions affectant les objets doivent être exécutées avant la déclaration des objets.
Renderman gère un environnement d'attributs appliqués aux objets. Cet environnement est initialisé avec des valeurs par défaut.
Définition des types courants
Type Renderman |
Type C |
RtBoolean |
short |
RtInt |
long |
RtFloat |
float |
RtVoid |
void |
RtString |
char * |
Types prédéfinis
Type prédéfini |
Définition |
RtPoint |
RtFloat[3] |
RtMatrix |
RtFloat[4][4] |
RtBound |
RtFloat[6] |
RtBasis |
RtFloat[4][4] |
RtPointer |
RtVoid * |
RtObjectHandle |
RtPointer |
RtLightHandle |
RtPointer |
RtToken |
char * |
RtColor |
RtFloat[3] |
Exemple 2
/* Copyrighted Pixar 1989 */
#include <ri.h>
RtPoint Square[4] =
{ { .5, .5,0},{ .5,-.5,0},
{-.5,-.5,0},{-.5, .5,0} };
static RtColor Color =
{ .2, .4, .6 };
void main(void) {
RiBegin(RI_NULL);
RiLightSource("distantlight",RI_NULL);
RiProjection("perspective",RI_NULL);
RiTranslate(0.0,0.0,1.0);
RiRotate(40.0,-1.0,1.0,0.0);
RiWorldBegin();
RiSurface("matte",RI_NULL);
RiColor(Color);
RiPolygon((RtInt) 4,RI_P,
(RtPointer) Square,
RI_NULL);
RiWorldEnd();
RiEnd();
}
- RiLightSource() : Définition d'une source lumineuse
RiProjection() : Définition du mode de projection
RiTranslate() et RiRotate() : définition des paramètres de visualisation. Toutes les surfaces définies par la suite sont transformées géométriquement.
RiColor() : Définition de la couleur de tracé

Exemple 3 : Un cube
Ces deux fonctions produisent le même objet: un cube de coté de taille 1.
/* Copyright Pixar 1989 */
#include <ri.h>
#define L -.5
#define R .5
#define D -.5
#define U .5
#define F .5
#define N -.5
void UnitCube(void) {
static RtPoint Cube[6][4] = {
{ {L,D,F},{L,D,N},{R,D,N},{R,D,F} },
{ {L,D,F},{L,U,F},{L,U,N},{L,D,N} },
{ {R,U,N},{L,U,N},{L,U,F},{R,U,F} },
{ {R,U,N},{R,U,F},{R,D,F},{R,D,N} },
{ {R,D,F},{R,U,F},{L,U,F},{L,D,F} },
{ {L,U,N},{R,U,N},{R,D,N},{L,D,N} } };
int i;
for( i = 0; i < 6; i++ )
RiPolygon((RtInt) 4,RI_P,
(RtPointer) Cube[i],
RI_NULL);
}
/* Copyrighted Pixar 1989 */
#include <ri.h>
void UnitCube(void) {
static RtPoint square[4] =
{ {.5, .5 ,.5},{-.5, .5,.5},
{-.5,-.5,.5},{.5 ,-.5,.5} };
RiPolygon((RtInt) 4,RI_P,
(RtPointer) square,RI_NULL);
RiRotate(90.0,0.0,1.0,0.0);
RiPolygon((RtInt) 4,RI_P,
(RtPointer) square,RI_NULL);
RiRotate(90.0,0.0,1.0,0.0);
RiPolygon((RtInt) 4,RI_P,
(RtPointer) square,RI_NULL);
RiRotate(90.0,0.0,1.0,0.0);
RiPolygon((RtInt) 4,RI_P,
(RtPointer) square,RI_NULL);
RiRotate(90.0,1.0,0.0,0.0);
RiPolygon((RtInt) 4,RI_P,
(RtPointer) square,RI_NULL);
RiRotate(180.0,1.0,0.0,0.0);
RiPolygon((RtInt) 4,RI_P,
(RtPointer) square,RI_NULL);
}

Exemple 4 : Une animation
/* Copyright Pixar 1989 */
#include <ri.h>
#include <stdio.h>
#define NFRAMES 10
#define NCUBES 5
#define FRAMEROT 5.0F
#define L -.5
#define R .5
#define D -.5
#define U .5
#define F .5
#define N -.5
void UnitCube(void) {
static RtPoint Cube[6][4] = {
{ {L,D,F},{L,D,N},{R,D,N},{R,D,F} },
{ {L,D,F},{L,U,F},{L,U,N},{L,D,N} },
{ {R,U,N},{L,U,N},{L,U,F},{R,U,F} },
{ {R,U,N},{R,U,F},{R,D,F},{R,D,N} },
{ {R,D,F},{R,U,F},{L,U,F},{L,D,F} },
{ {L,U,N},{R,U,N},{R,D,N},{L,D,N} } };
for( int i = 0 ; i < 6 ; i++ )
RiPolygon((RtInt) 4,RI_P,
(RtPointer) Cube[i],
RI_NULL);
}
void ColorCube(int n,float s) {
int x, y, z;
RtColor cl;
if( n<=0 )
return;
RiAttributeBegin();
RiTranslate(-.5,-.5,-.5);
RiScale(1.0F/n,1.0F/n,1.0F/n);
for( x = 0 ; x < n ; x++ )
for( y = 0 ; y < n ; y++ )
for( z = 0 ; z < n ; z++ ) {
cl[0] = ((float) x+1)/((float) n);
cl[1] = ((float) y+1)/((float) n);
cl[2] = ((float) z+1)/((float) n);
RiColor(cl);
RiTransformBegin();
RiTranslate(x+.5F,y+.5F,z+.5F);
RiScale(s,s,s);
UnitCube();
RiTransformEnd(); }
RiAttributeEnd();
}
void main(void) {
RtInt fr;
float scale;
char filename[20];
RiBegin(RI_NULL);
for ( fr = 1 ; fr <= NFRAMES ; fr++ ) {
sprintf(filename,"anim.%d.tiff",fr);
RiFrameBegin(fr);
RiLightSource("distantlight",RI_NULL);
RiProjection("perspective",RI_NULL);
RiTranslate(0.0,0.0,1.5);
RiRotate(40.0,-1.0,1.0,0.0);
RiDisplay(filename,RI_FILE,
RI_RGBA,RI_NULL);
RiFormat((RtInt) 256,(RtInt) 192,-1.0);
RiShadingRate(1.0);
RiWorldBegin();
RiSides((RtInt) 1);
scale =(float)(NFRAMES-(fr-1))/NFRAMES;
RiRotate(FRAMEROT*fr,0.0,0.0,1.0);
RiSurface("matte",RI_NULL);
ColorCube(NCUBES,scale);
RiWorldEnd();
RiFrameEnd(); }
RiEnd();
}
RiFrameBegin(): Début du tracé d'une image
RiFrameEnd(): Fin du tracé d'une image
L'environnement est sauvegardé avant RiFrameBegin et restauré après RiFrameEnd.
RiFormat(): Fixe les résolutions horizontale et verticale d'une image, ainsi que l'aspect ratio (-1 -> valeur par défaut de l'architecture)
RiShadingRate(): Fixe la fréquence d’échantillonnage
RiSides() : Fixe le nombre de faces visibles d'une surface
Les primitives graphiques
Les surfaces quadriques
Sphère, cône, cylindre, hyperboloïde, paraboloïde et tore
RiSphere()
RiCone
RiCylinder()
RiHyperboloid()
RiParaboloid()
RiTorus()
Toutes les quadriques sont des surfaces de révolution autour de l'axe z -> utilisation d'un angle pour indiquer la portée de cette rotation (si angle différent de 360° -> surface non fermée).
Attention!!! Ces quadriques sont des surfaces et non des volumes.
Exemple
RiSphere(rayon,zmin,zmax,theta,parameterlist)
RtFloat rayon
RtFloat zmin,zmax
RtFloat theta
Génère une sphère de rayon rayon sur theta degrés, centrée sur l'origine, tronquée à z = zmin, et z = zmax.
Exemple
/* Copyrighted Pixar 1989 */
#include <ri.h>
#define OFFSET 1.2
void ShowQuads(void) {
RtPoint hyperpt1, hyperpt2;
RiRotate(-90.0,1.0,0.0,0.0);
RiTranslate(-OFFSET,0.0,(OFFSET/2));
RiSphere(0.5,-0.5,0.5,360.0,RI_NULL);
RiTranslate(OFFSET,0.0,0.0);
RiTranslate(0.0,0.0,-0.5);
RiCone(1.0,0.5,360.0,RI_NULL);
RiTranslate(0.0,0.0,0.5);
RiTranslate(OFFSET,0.0,0.0);
RiCylinder(0.5,-0.5,0.5,360.0,RI_NULL);
RiTranslate(-(OFFSET*2),0.0,-OFFSET);
hyperpt1[0] = 0.4;
hyperpt1[1] = -0.4;
hyperpt1[2] = -0.4;
hyperpt2[0] = 0.4;
hyperpt2[1] = 0.4;
hyperpt2[2] = 0.4;
RiHyperboloid(hyperpt1,hyperpt2,
360.0,RI_NULL);
RiTranslate(OFFSET, 0.0, -0.5);
RiParaboloid(0.5,0.0,0.9,360.0,RI_NULL);
RiTranslate(OFFSET,0.0,0.5);
RiTorus(.4,.15,0.0,360.0,360.0,RI_NULL);
}

Exemple
/* Copyrighted Pixar 1989 */
/* From the RenderMan Companion */
#include <ri.h>
#include <stdio.h>
typedef struct { RtFloat x,y;} Point2D;
#define NPOINTS 16
RtColor color = {.9F,.9F,.5F};
Point2D points[NPOINTS] = {
{1.5000F,.0000F},
{1.4600F,.0900F},
{1.3500F,.1273F},
{1.2625F,.1203F},
{1.1750F,.1047F},
{1.0875F,.0935F},
{1.0000F,.0899F},
{0.9375F,.0982F},
{0.8625F,.1236F},
{0.7250F,.1851F},
{0.5875F,.2281F},
{0.4500F,.2383F},
{0.3375F,.2255F},
{0.2250F,.1953F},
{0.0750F,.1414F},
{0.0000F,.1125F} };
void SurfOR(Point2D *points,int npoints) {
int pt;
RtPoint point1,point2;
RtFloat *pp1,*pp2,*tmp;
pp1 = point1;
pp2 = point2;
pp1[0] = points[0].y;
pp1[1] = 0;
pp1[2] = points[0].x;
for ( pt = 1 ; pt < npoints ; pt++ ) {
pp2[0] = points[pt].y;
pp2[1] = 0;
pp2[2] = points[pt].x;
RiHyperboloid(pp1,pp2,360.0,RI_NULL);
tmp = pp1; pp1 = pp2; pp2 = tmp; }
}
void Go(void) {
RiColor(color);
RiRotate(-90.0,1.0,0.0,0.0);
RiScale(2.5,2.5,2.5);
SurfOR(points,NPOINTS);
}
void main(void) {
RiBegin(RI_NULL);
RiFormat(300,450,1.0F);
RiDisplay("Quille.tif",RI_FILE,
RI_RGB,RI_NULL);
RiLightSource("distantlight",RI_NULL);
RtFloat fov = 45.0F ;
RiProjection("perspective",RI_FOV,
(RtPointer) &fov,RI_NULL);
RiTranslate(0.0F,-1.8F,4.0F);
RiWorldBegin();
RiSurface("matte",RI_NULL);
Go();
RiWorldEnd();
RiEnd();
}
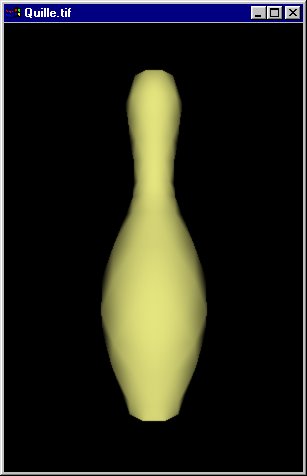
Quille de bowling créée par assemblage d'hyperboloïdes.

Les polygones et les polyèdres
Les polygones
Polygones 3D de différents types:
planaire, non planaire
convexe, concave
Fonctions de génération de polygones :
RiPolygon(): Planaire et convexe
RiGeneralPolygon(): Quelconque
RiPolygon(RtInt n,parameterlist): Génération d'un polygone 3D de sommets
le token RI_P permet de passer la liste des sommets.
Faute d'autres informations, la normale affectée à chaque sommet est la normale à la facette -> teinte constante.
Exemple
/* Copyrighted Pixar 1989 */
/* From the RenderMan Companion */
#include <ri.h>
#include <stdio.h>
#include <math.h>
typedef struct { RtFloat x,y;} Point2D;
#define NPOINTS 16
RtColor color = {.9F,.9F,.5F};
Point2D points[NPOINTS] = {
{1.5000F,.0000F},
{1.4600F,.0900F},
{1.3500F,.1273F},
{1.2625F,.1203F},
{1.1750F,.1047F},
{1.0875F,.0935F},
{1.0000F,.0899F},
{0.9375F,.0982F},
{0.8625F,.1236F},
{0.7250F,.1851F},
{0.5875F,.2281F},
{0.4500F,.2383F},
{0.3375F,.2255F},
{0.2250F,.1953F},
{0.0750F,.1414F},
{0.0000F,.1125F} };
#define PI 3.14159F
#define SWAP(a,b,temp) temp = a;a = b;b = temp;
#define CP(d,s) {d[0]=s[0];d[1]=s[1];d[2]=s[2];}
#define NDIVS 8
void getnextpair(float offset,
RtPoint *ptrnp,
RtFloat *point0,
RtFloat *point1,
int ndivs) {
float r;
r = 2*PI*offset/ndivs;
ptrnp[0][0] = point0[0]*(float) sin(r);
ptrnp[0][1] = point0[0]*(float) cos(r);
ptrnp[0][2] = point0[2];
r = 2*PI*(offset-.5F)/ndivs;
ptrnp[1][0] = point1[0]*(float) sin(r);
ptrnp[1][1] = point1[0]*(float) cos(r);
ptrnp[1][2] = point1[2];
}
void PolyBoid(RtFloat *point0,
RtFloat *point1,
int ndivs,
int parity) {
RtPoint vertexpair0[2];
RtPoint vertexpair1[2];
RtPoint *ptrnp = vertexpair0;
RtPoint *ptrlastpair = vertexpair1;
RtPoint *temp;
RtPoint triangle[3];
getnextpair(0+parity/2.0F,ptrnp,
point0,point1,ndivs);
for ( int i = 1 ; i <= ndivs ; i++ ) {
SWAP(ptrlastpair,ptrnp,temp)
getnextpair(i+parity/2.0F,ptrnp,
point0,point1,ndivs);
CP(triangle[0],ptrlastpair[0]);
CP(triangle[1],ptrlastpair[1]);
CP(triangle[2],ptrnp[1]);
RiPolygon((RtInt) 3,RI_P,
(RtPointer) triangle,RI_NULL);
CP(triangle[0],ptrnp[0]);
CP(triangle[1],ptrnp[1]);
CP(triangle[2],ptrlastpair[0]);
RiPolygon((RtInt) 3,RI_P,
(RtPointer) triangle,
RI_NULL); }
}
void PolySurfOR(Point2D *points,
int npoints) {
int pt;
RtPoint point1,point2;
RtFloat *pp1,*pp2,*tmp;
pp1 = point1;
pp2 = point2;
pp1[0] = points[0].y;
pp1[1] = 0;
pp1[2] = points[0].x;
for ( pt = 1 ; pt < npoints-1 ; pt++ ) {
pp2[0] = points[pt].y;
pp2[1] = 0;
pp2[2] = points[pt].x;
PolyBoid(pp1,pp2,NDIVS,pt-1);
tmp = pp1;
pp1 = pp2;
pp2 = tmp; }
pt = npoints-1;
pp2[0] = points[pt].y;
pp2[1] = 0;
pp2[2] = points[pt].x;
PolyBoid(pp1,pp2,NDIVS,pt-1);
}
void Go(void) {
RiColor(color);
RiRotate(-90.0,1.0,0.0,0.0);
RiScale(2.5,2.5,2.5);
PolySurfOR(points,NPOINTS);
}
void main(void) {
RiBegin(RI_NULL);
RiFormat(300,450,1.0F);
RiDisplay("Quille.tif",
RI_FILE,RI_RGB,RI_NULL);
RiLightSource("distantlight",RI_NULL);
RtFloat fov = 45.0F ;
RiProjection("perspective",RI_FOV,
(RtPointer) &fov,RI_NULL);
RiTranslate(0.0F,-1.8F,4.0F);
RiWorldBegin();
RiSurface("matte",RI_NULL);
Go();
RiWorldEnd();
RiEnd();
}
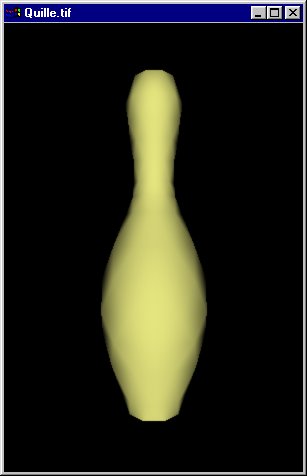
Ce programme fournit une quille de bowling facettisée.

Le token RI_N permet de passer la liste des normales associées aux sommets.
Cette liste est prise en compte au cours de l'affichage de la facette -> obtention éventuelle d'une teinte non constante.
Exemple
/* Copyrighted Pixar 1989 */
#include <ri.h>
#include <stdio.h>
#include <math.h>
typedef struct { RtFloat x,y;} Point2D;
#define NPOINTS 16
RtColor color = {.9F,.9F,.5F};
Point2D points[NPOINTS] = {
{1.5000F,.0000F},
{1.4600F,.0900F},
{1.3500F,.1273F},
{1.2625F,.1203F},
{1.1750F,.1047F},
{1.0875F,.0935F},
{1.0000F,.0899F},
{0.9375F,.0982F},
{0.8625F,.1236F},
{0.7250F,.1851F},
{0.5875F,.2281F},
{0.4500F,.2383F},
{0.3375F,.2255F},
{0.2250F,.1953F},
{0.0750F,.1414F},
{0.0000F,.1125F} };
#define PI 3.14159F
#define NDIVS 8
#define SWAP(a,b,temp) temp = a;a = b;b = temp;
#define CP(d,s) {d[0]=s[0];d[1]=s[1];d[2]=s[2];}
void getnextpair(float offset,
RtPoint *ptrnp,
RtFloat *point0,
RtFloat *point1,
int ndivs) {
float r = 2*PI*offset/ndivs;
ptrnp[0][0] = point0[0]*(float) sin(r);
ptrnp[0][1] = point0[0]*(float) cos(r);
ptrnp[0][2] = point0[2];
r = 2*PI*(offset-.5F)/ndivs;
ptrnp[1][0] = point1[0]*(float) sin(r);
ptrnp[1][1] = point1[0]*(float) cos(r);
ptrnp[1][2] = point1[2];
}
void PolyBoid(RtFloat *point0,
RtFloat *point1,
RtFloat *normal0,
RtFloat *normal1,
int ndivs,
int parity) {
RtPoint vertexpair0[2];
RtPoint vertexpair1[2];
RtPoint *ptrnextvertex = vertexpair0;
RtPoint *ptrlastvertex = vertexpair1;
RtPoint *temp;
RtPoint vertextriangle[3];
RtPoint normalpair0[2];
RtPoint normalpair1[2];
RtPoint *ptrnextnormal = normalpair0;
RtPoint *ptrlastnormal = normalpair1;
RtPoint normaltriangle[3];
getnextpair(0+parity/2.0F,ptrnextvertex,
point0,point1,ndivs);
getnextpair(0+parity/2.0F,ptrnextnormal,
normal0,normal1,ndivs);
for ( int i = 1 ; i <= ndivs ; i++ ) {
SWAP(ptrlastvertex,ptrnextvertex,temp)
SWAP(ptrlastnormal,ptrnextnormal,temp)
getnextpair(i+parity/2.0F,ptrnextvertex,
point0,point1,ndivs);
getnextpair(i+parity/2.0F,ptrnextnormal,
normal0,normal1,ndivs);
CP(vertextriangle[0],ptrlastvertex[0]);
CP(vertextriangle[1],ptrlastvertex[1]);
CP(vertextriangle[2],ptrnextvertex[1]);
CP(normaltriangle[0],-ptrlastnormal[0]);
CP(normaltriangle[1],-ptrlastnormal[1]);
CP(normaltriangle[2],-ptrnextnormal[1]);
RiPolygon((RtInt) 3,
RI_P,(RtPointer) vertextriangle,
RI_N,(RtPointer) normaltriangle,
RI_NULL);
CP(vertextriangle[0],ptrnextvertex[0]);
CP(vertextriangle[1],ptrnextvertex[1]);
CP(vertextriangle[2],ptrlastvertex[0]);
CP(normaltriangle[0],ptrnextnormal[0]);
CP(normaltriangle[1],ptrnextnormal[1]);
CP(normaltriangle[2],ptrlastnormal[0]);
RiPolygon((RtInt) 3,
RI_P,(RtPointer) vertextriangle,
RI_N,(RtPointer) normaltriangle,
RI_NULL); }
}
void PolySurfOR(Point2D *points,int npoints) {
int pt;
RtPoint point1,point2,normal1,normal2;
RtFloat *pp1,*pp2,*pm1,*pm2,*tmp;
pp1 = point1;
pp2 = point2;
pm1 = normal1;
pm2 = normal2;
pp1[0] = points[0].y;
pp1[1] = 0;
pp1[2] = points[0].x;
pm1[0] = points[0].x - points[1].x;
pm1[1] = 0;
pm1[2] = points[1].y - points[0].y;
for ( pt = 1 ; pt < npoints-1 ; pt++ ) {
pp2[0] = points[pt].y;
pp2[1] = 0;
pp2[2] = points[pt].x;
pm2[0] = points[pt-1].x - points[pt+1].x;
pm2[1] = 0;
pm2[2] = points[pt+1].y - points[pt-1].y;
PolyBoid(pp1,pp2,pm1,pm2,8,pt-1);
tmp = pp1;
pp1 = pp2;
pp2 = tmp;
tmp = pm1;
pm1 = pm2;
pm2 = tmp; }
pt = npoints-1;
pp2[0] = points[pt].y;
pp2[1] = 0;
pp2[2] = points[pt].x;
pm2[0] = points[pt-1].x - points[pt].x;
pm2[1] = 0;
pm2[2] = points[pt].y - points[pt-1].y;
PolyBoid(pp1,pp2,pm1,pm2,8,pt-1);
}
void Go(void) {
RiColor(color);
RiRotate(-90.0,1.0,0.0,0.0);
RiScale(2.5,2.5,2.5);
PolySurfOR(points,NPOINTS);
}
void main(void) {
RiBegin(RI_NULL);
RiFormat(300,450,1.0F);
RiDisplay("Quille.tif",
RI_FILE,RI_RGB,
RI_NULL);
RiLightSource("distantlight",RI_NULL);
RtFloat fov = 45.0F ;
RiProjection("perspective",
RI_FOV,(RtPointer) &fov,
RI_NULL);
RiTranslate(0.0F,-1.8F,4.0F);
RiWorldBegin();
RiSurface("matte",RI_NULL);
Go();
RiWorldEnd();
RiEnd();
}
Définition d'un polyèdre à partir d'un ensemble de facettes où les mêmes points n'apparaissent pas plus d'une fois.
RiPointsPolygons : définition d'un objet composé de facettes
void RiPointsPolygons(RtInt n,RtInt *nv,RtInt *v,paramlist)
n : nombre de polygones
nv : nombre de sommets de chaque polygone
v : liste des indices des sommets des polygones
Token :
RI_P : Position des sommets
RI_N : Normales aux sommets
Exemple
RiPolygon(4,RI_P,(RtPointer)
p,RI_NULL) ;
<=>
RiPointsPolygon(1,n,v,RI_P,(RtPointer)p,RI_NULL);
n est un tableau à 1 élément de valeur 4.
verts est un tableau de 4 éléments tels que v[i] = i.
Exemple
/* Copyrighted Pixar 1989 */
#include <ri.h>
#include <stdio.h>
#include <math.h>
typedef struct { RtFloat x,y;} Point2D;
#define NPOINTS 16
RtColor color = {.9F,.9F,.5F};
Point2D points[NPOINTS] = {
{1.5000F,.0000F},
{1.4600F,.0900F},
{1.3500F,.1273F},
{1.2625F,.1203F},
{1.1750F,.1047F},
{1.0875F,.0935F},
{1.0000F,.0899F},
{0.9375F,.0982F},
{0.8625F,.1236F},
{0.7250F,.1851F},
{0.5875F,.2281F},
{0.4500F,.2383F},
{0.3375F,.2255F},
{0.2250F,.1953F},
{0.0750F,.1414F},
{0.0000F,.1125F} };
#define PI 3.14159F
#define NDIVS 8
#define SWAP(a,b,temp) temp = a;a = b;b = temp;
#define CP(d,s) {d[0]=s[0];d[1]=s[1];d[2]=s[2];}
#define MAXVERTS 100
RtPoint vertexstrip[MAXVERTS][2];
RtPoint normalstrip[MAXVERTS][2];
RtInt nverts[MAXVERTS][2];
RtInt indices[MAXVERTS][2][3];
void getnextpair(float offset,
RtPoint *ptrnextpair,
RtFloat *point0,
RtFloat *point1,
int ndivs) {
float r;
r = 2*PI*offset/ndivs;
ptrnextpair[0][0] = point0[0]*(float) sin(r);
ptrnextpair[0][1] = point0[0]*(float) cos(r);
ptrnextpair[0][2] = point0[2];
r = 2*PI*(offset-.5F)/ndivs;
ptrnextpair[1][0] = point1[0]*(float) sin(r);
ptrnextpair[1][1] = point1[0]*(float) cos(r);
ptrnextpair[1][2] = point1[2];
}
void getnextpair2(float offset,
RtPoint *ptrnextpair,
RtFloat *point0,
RtFloat *point1,
int ndivs) {
float r;
r = 2*PI*offset/ndivs;
ptrnextpair[0][0] = -point0[0]*(float) sin(r);
ptrnextpair[0][1] = -point0[0]*(float) cos(r);
ptrnextpair[0][2] = -point0[2];
r = 2*PI*(offset-.5F)/ndivs;
ptrnextpair[1][0] = -point1[0]*(float) sin(r);
ptrnextpair[1][1] = -point1[0]*(float) cos(r);
ptrnextpair[1][2] = -point1[2];
}
void PolyBoid(RtFloat *point0,
RtFloat *point1,
RtFloat *normal0,
RtFloat *normal1,
int ndivs,
int parity) {
for ( int i = 0 ; i <= ndivs ; i++ ) {
getnextpair(i+parity/2.0F,
vertexstrip[i],
point0,point1,
ndivs);
getnextpair2(i+parity/2.0F,
normalstrip[i],
normal0,normal1,
ndivs); }
for (i = 0 ; i < ndivs ; i++ ) {
nverts[i][0] = nverts[i][1] = 3;
indices[i][0][0] = i*2;
indices[i][0][1] = i*2+1;
indices[i][0][2] = (i+1)*2+1;
indices[i][1][0] = (i+1)*2+1;
indices[i][1][1] = (i+1)*2;
indices[i][1][2] = i*2; }
RiPointsPolygons((RtInt) (ndivs*2),
(RtInt *) nverts,
(RtInt *) indices,
RI_P,(RtPointer) vertexstrip,
RI_N,(RtPointer) normalstrip,
RI_NULL);
}
void PolySurfOR(Point2D *points,int npoints) {
RtPoint point1,point2;
RtFloat *pp1,*pp2,*tmp;
RtPoint normal1,normal2;
RtFloat *pm1,*pm2;
pp1 = point1;
pp2 = point2;
pm1 = normal1;
pm2 = normal2;
pp1[0] = points[0].y;
pp1[1] = 0;
pp1[2] = points[0].x;
pm1[0] = points[0].x - points[1].x;
pm1[1] = 0;
pm1[2] = points[1].y - points[0].y;
for ( int pt = 1 ; pt < npoints-1 ; pt++ ) {
pp2[0] = points[pt].y;
pp2[1] = 0;
pp2[2] = points[pt].x;
pm2[0] = points[pt-1].x - points[pt+1].x;
pm2[1] = 0;
pm2[2] = points[pt+1].y - points[pt-1].y;
PolyBoid(pp1,pp2,pm1,pm2,NDIVS,pt-1);
tmp = pp1;
pp1 = pp2;
pp2 = tmp;
tmp = pm1;
pm1 = pm2;
pm2 = tmp; }
pt = npoints-1;
pp2[0] = points[pt].y;
pp2[1] = 0;
pp2[2] = points[pt].x;
pm2[0] = points[pt-1].x - points[pt].x;
pm2[1] = 0;
pm2[2] = points[pt].y - points[pt-1].y;
PolyBoid(pp1,pp2,pm1,pm2,NDIVS,pt-1);
}
void Go(void) {
RiColor(color);
RiRotate(-90.0,1.0,0.0,0.0);
RiScale(2.5,2.5,2.5);
PolySurfOR(points,NPOINTS);
}
void main(void) {
RiBegin(RI_NULL);
RiFormat(300,450,1.0F);
RiDisplay("Quille.tif",
RI_FILE,RI_RGB,
RI_NULL);
RiLightSource("distantlight",RI_NULL);
RtFloat fov = 45.0F ;
RiProjection("perspective",
RI_FOV,(RtPointer) &fov,
RI_NULL);
RiTranslate(0.0F,-1.8F,4.0F);
RiWorldBegin();
RiSurface("matte",RI_NULL);
Go();
RiWorldEnd();
RiEnd();
}
Surfaces bilinéaire et bicubiques
Deux types de surfaces (patch) paramétriques:
- les surfaces bilinéaires -> pas de lissage car créées par interpolation linéaire entre quatre points
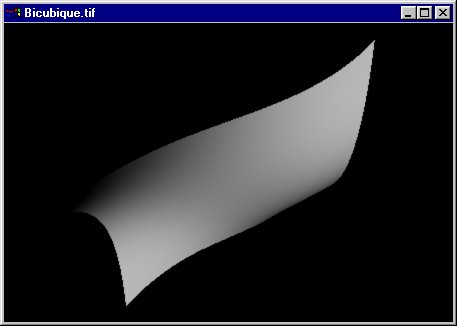
- Les surfaces paramétriques bicubiques -> lissage à partir d'un vecteur géométrique de 16 points
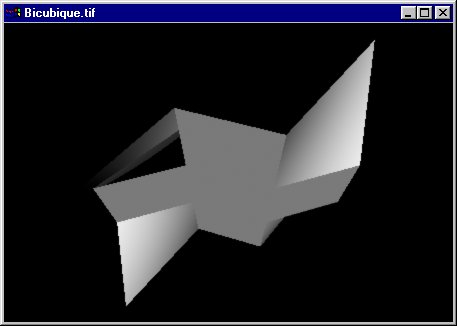
void RiPatch(RtToken type,parameterlist) ;
RtToken : RI_BICUBIC ou RI_BILINEAR
la parameterlist devra au minimum contenir les sommets définissant le patch:
un tableau de 4 sommets pour une surface bilinéaire,
un tableau de 16 sommets pour une surface bicubique,
précédé du token RI_P.
La surface d'un patch bicubique est lissée géométriquement mais aussi lissée vis à vis de l'éclairage.
-> On n'a plus a fournir de normales.
Exemple
/* Copyrighted Pixar 1989 */
#include <ri.h>
#include <stdio.h>
#define MV(d,s) {d[0]=s[0];d[1]=s[1];d[2]=s[2];}
#define HULL 1
#define X0 -1.0F
#define X1 -.33F
#define X2 .33F
#define X3 1.0F
#define Y0 -.7F
#define Y1 -.1F
#define Y2 0.1F
#define Y3 0.7F
#define Z0 -1.0F
#define Z1 -.33F
#define Z2 .33F
#define Z3 1.0F
void PatchExample(RtPoint Patch[4][4]) {
#ifdef PATCH
RiPatch(RI_BICUBIC,
RI_P,(RtPointer) Patch,
RI_NULL);
#endif
#ifdef HULL
RtPoint blpatch[2][2];
for ( int v = 0 ; v < 3 ; v++ ) {
for (int u = 0 ; u < 3 ; u++ ) {
MV(blpatch[0][0],Patch[v][u])
MV(blpatch[0][1],Patch[v][u+1])
MV(blpatch[1][0],Patch[v+1][u])
MV(blpatch[1][1],Patch[v+1][u+1])
RiPatch(RI_BILINEAR,
RI_P, (RtPointer) blpatch,
RI_NULL); } }
#endif
}
void DoCatmullRomPatch(RtPoint patch[4][4]) {
RiBasis(RiCatmullRomBasis,RI_CATMULLROMSTEP,
RiCatmullRomBasis,RI_CATMULLROMSTEP);
RiPatch(RI_BICUBIC,
RI_P,(RtPointer) patch,
RI_NULL);
}
void Go(void) {
staticRtPointPatch[4][4]={
{{X0,Y0,Z0},{X1,Y2,Z0},
{X2,Y1,Z0},{X3,Y3,Z0}},
{{X0,Y1,Z1},{X1,Y2,Z1},
{X2,Y1,Z1},{X3,Y2,Z1}},
{{X0,Y1,Z2},{X1,Y2,Z2},
{X2,Y1,Z2},{X3,Y2,Z2}},
{{X0,Y0,Z3},{X1,Y2,Z3},
{X2,Y1,Z3},{X3,Y3,Z3}}};
#ifdef CATMULLROM
DoCatmullRomPatch(Patch);
#else
PatchExample(Patch);
#endif
}
void main(void) {
RiBegin(RI_NULL);
RiFormat(450,300,1.0F);
RiDisplay("Bicubique.tif",
RI_FILE,RI_RGB,
RI_NULL);
RiLightSource("distantlight",RI_NULL);
RtFloat fov = 45.0F ;
RiProjection("perspective",
RI_FOV,(RtPointer) &fov,
RI_NULL);
RiTranslate(0.0F,-0.2F,3.0F);
RiRotate(30.0F,1.0F,0.0F,0.0F);
RiWorldBegin();
RiSurface("matte",RI_NULL);
Go();
RiWorldEnd();
RiEnd();
}
Plusieurs surfaces bicubiques sont utilisables :
Hermite,
Catmull-Rom,
Bezier,
B-spline,
tant pour le premier axe que pour le second.
La fonction RiBasis() permet la sélection des matrices de base désirées.
void RiBasis(RtBasis ub,RtInt us,RtBasis vb,RtInt vs);
ub,vb |
us,vs |
RiHermiteBasis |
RI_HERMITESTEP |
RiCatmullRomBasis |
RI_CATMULLROMSTEP |
RiBezierBasis |
RI_BEZIERSTEP |
RiBSplineBasis |
RI_BSPLINESTEP |
Exemple
void DoCatmullRomPatch(RtPoint
patch[4][4]) {
RiBasis(RiCatmullRomBasis,
RI_CATMULLROMSTEP,
RiCatmullRomBasis,
RI_CATMULLROMSTEP);
RiPatch(RI_BICUBIC,
RI_P,(RtPointer) patch,
RI_NULL);
}
But : Modélisation d'un objet sous la forme d'un maillage quadrangulaire permettant l'obtention d'une surface lissée par dessin de patchs les uns à coté des autres dans les deux directions.
void RiPatchMesh(RtToken t,RtInt nu,RtToken uw,RtInt nv,RtToken vw,parameterlist);
t : type du maillage (RI_BICUBIQUE ou RI_BILINEAR)
nu, nv : nombre de points du maillage (selon chacun des axes)
uw,vw : périodicité selon les 2 axes ("periodic" ou "nonperiodic")
La périodicité permet de représenter des objets fermés sans que la fermeture soit visible par une rupture de l'éclairage.
Exemple
/* Copyrighted Pixar 1989 */
/* From the RenderMan Companion */
#include <ri.h>
#include <stdio.h>
typedef struct { RtFloat x,y;} Point2D;
#define NPOINTS 10
Point2D points[NPOINTS] = {
{.0000F,1.5000F},
{.0703F,1.5000F},
{.1273F,1.4293F},
{.1273F,1.3727F},
{.1273F,1.2300F},
{.0899F,1.1600F},
{.0899F,1.0000F},
{.0899F,0.7500F},
{.4100F,0.6780F},
{.1250F,0.0000F}};
#define NU 13
#define MAXNPTS 100
#define F .5522847F
float coeff[NU][2] = {
{ 1.0F,0.0F },{ 1.0F,F },
{ F,1.0F },{ 0,1.0F },
{-F,1.0F },{-1.0F,F },
{-1.0F,0.0F },{-1.0F,-F },
{-F,-1.0F },{ 0,-1.0F },
{ F,-1.0F },{ 1.0F,-F },{ 1.0F,0} };
RtPoint mesh[MAXNPTS][NU];
RtColor color = {.9F,.9F,.5F};
void SurfOR(Point2D points[],int npoints) {
for ( int v = 0 ; v < npoints ; v++) {
for ( int u = 0 ; u < NU ; u++ ) {
mesh[v][u][0] = points[v].x*coeff[u][0];
mesh[v][u][1] = points[v].x*coeff[u][1];
mesh[v][u][2] = points[v].y; } }
RiBasis(RiBezierBasis,
RI_BEZIERSTEP,
RiBezierBasis,
RI_BEZIERSTEP);
RiPatchMesh(RI_BICUBIC,
(RtInt) NU,RI_NONPERIODIC,
(RtInt) npoints,RI_NONPERIODIC,
RI_P,(RtPointer) mesh,
RI_NULL);
}
void Go(void) {
RiColor(color);
RiRotate(-90.0,1.0,0.0,0.0);
RiScale(2.5,2.5,2.5);
SurfOR(points,NPOINTS);
}
void main(void) {
RiBegin(RI_NULL);
RiFormat(300,450,1.0F);
RiDisplay("Quille.tif",
RI_FILE,RI_RGB,
RI_NULL);
RiLightSource("distantlight",RI_NULL);
RtFloat fov = 45.0F ;
RiProjection("perspective",
RI_FOV,(RtPointer) &fov,
RI_NULL);
RiTranslate(0.0F,-1.8F,4.0F);
RiWorldBegin();
RiSurface("matte",RI_NULL);
Go();
RiWorldEnd();
RiEnd();
}
