Sujets et Corrections
de TD et TP
![]()
|
Fichier zip |
TD n°1 et n°2 : Premières scènes OpenGL
Exercice n°1
(1) Programmer en OpenGL la scène suivante sous la forme d'une fonction C sans utiliser les fonctions glPushMatrix
et glPopMatrix ailleurs qu'en début et fin de fonction:
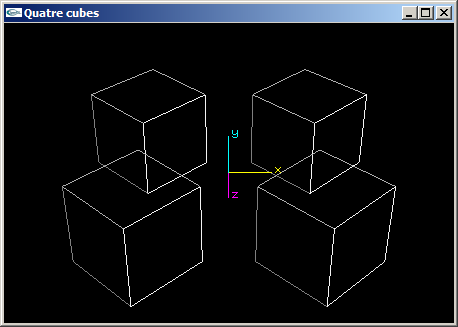
Quatre cubes de coté 2.0 aux positions (2.0,0.0,2.0), (2.0,0.0,-2.0), (-2.0,0.0,2.0) et (-2.0,0.0,-2.0).
(2) Reprogrammer en OpenGL la scène de la question (1) de telle manière que les cubes aient une de leurs faces orientée vers l'origine du repère.
(3) Reprogrammer en OpenGL la scène de la question (2) en utilisant les fonctions glPushMatrix et glPopMatrix pour rendre les objets indépendants les uns des autres et simplifier l'écriture de la fonction scène.

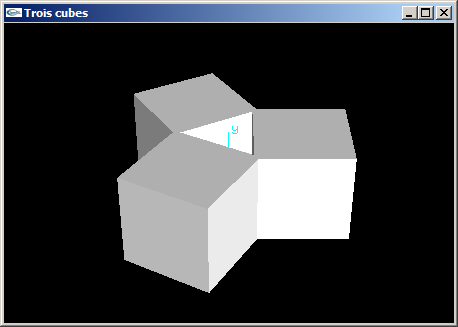
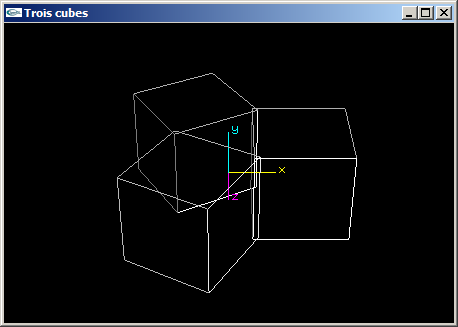
(4) Programmer une scène OpenGL en plaçant 3 cubes de coté 2.0 aux 3 sommets d'un triangle équilatéral
défini avec les caractéristiques suivantes:
- rayon 1.5,
- centré sur l'origine,
- plongé dans le plan xOz.
Les 3 cubes présentent une de leurs faces orientée vers l'origine.
Exercice n°2
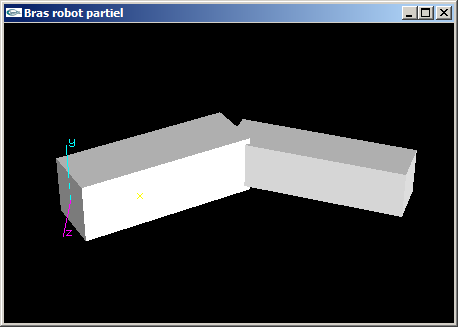
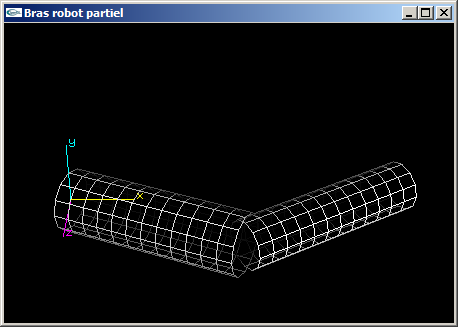
(1) Programmer la scène OpenGL modélisant un bras robot simplifié composé d'un avant-bras et
d'un bras.
L'avant-bras est articulé pour que sa base puisse tourner autour de l'axe Oy d'un angle r1. Il s'agit d'un parallélépipède
rectangle de dimension (3.0,1.0,1.0).
Le bras est articulé autour de l'axe y au bout de l'avant bras pour un angle r2. Il s'agit d'un parallélépipède
rectangle de dimension (3.0,0.8,0.8).

(2) Modifier la fonction OpenGL de l'exercice n°1 en remplaçant les parallélépipèdes par des cylindres de tailles équivalentes.

Exercice 3
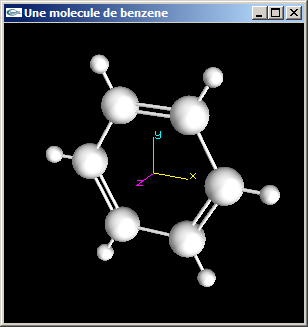
a) Implanter en OpenGL une fonction de dessin d'une molécule de Benzène (C6H6).

Les atomes de carbone (atome centraux) ont un rayon égal à 0.5.
Les liaisons entre 2 atomes de carbone ont pour longueur (centre à centre) 2.0 et pour rayon 0.15.
Les atomes d'hydrogène ont un rayon égal à 0.25.
Les liaisons entre atome de carbone et d'hydrogène ont pour longueur (centre à centre) 1.2 et pour rayon 0.05.
La molécule est centrée sur l'origine et placée dans le plan xOy.
b) Modifier la modélisation de la molécule de benzène de la question précédente pour
que les liaisons carbone-carbone soient alternativement des liaisons simples et des liaisons doubles (voir figure ci-dessous).
Les cylindres modélisant ces liaisons auront pour rayon 0.05 (comme les liaisons carbone-hydrogène). Dans
le cas des liaisons doubles, les deux cylindres de modélisation seront écartés de 0.1.
Solutions
| Quatre cubes (Question 3) |
| Trois cubes |
| Bras robot avec parallélépipèdes |
| Bras robot avec cylindres |
| Molécule de benzène |
![]()
TD n°3 : Modélisation par facettes
Exercice n°1
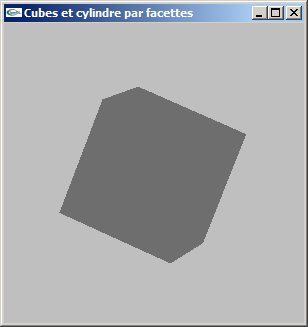
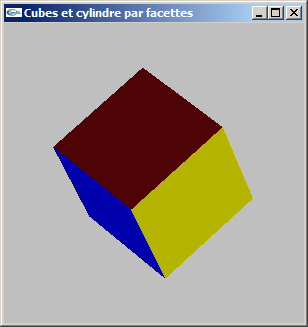
a) Modéliser par facettes un cube de coté c centré sur l'origine du repère de modélisation.
On ne générera pas les normales.
La fonction créée aura pour prototype:
void mySolidCube(float c);
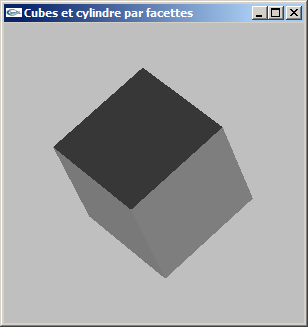
b) Modifier la modélisation de la question précédente pour ajouter la gestion
des normales.
Le but est de rendre possible les calculs d'éclairage.
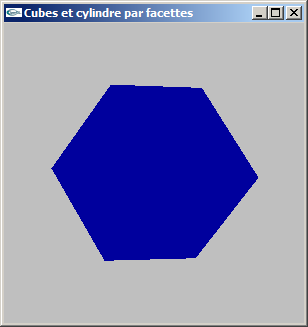
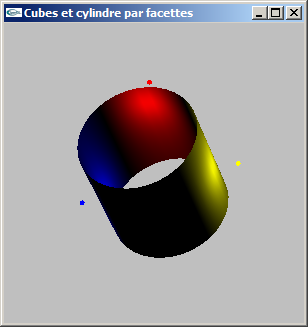
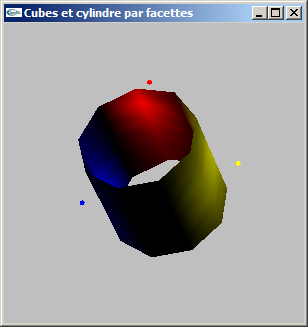
a) Modéliser par facettes un cylindre selon les caractéristiques suivantes:
- choix du rayon,
- choix de la hauteur,
- choix du nombre de facettes en découpage longitudinal pour une valeur entière ns,
- centré sur l'origine du repère de modélisation,
- axé selon y.
On ne modélisera pas les bases du cylindre, mais uniquement le tube.
La fonction créée aura pour prototype:
void mySolidCylinder(float hauteur, float rayon, int ns);
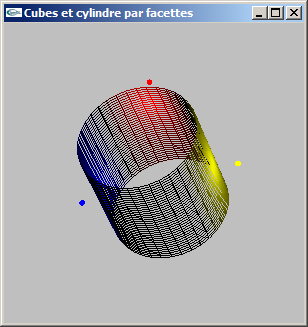
b) Ajouter un découpage latéral (selon l'axe y) pour une valeur nl.
Le prototype de la fonction devient:
void mySolidCylinder(float hauteur, float rayon, int ns, int nl);
Solutions
![]()
TP n°1 : Premiers programmes OpenGL
Création d'un projet Visual C++ permettant la compilation OpenGL:
- Les fichiers d'inclusion (nécessaires à la compilation) spécifiques à OpenGL sont GL/gl.h et GL/glu.h ainsi que GL/glut.h si GLUT est utilisé.
- Les librairies d'édition de liens (nécessaires à la création de l'exécutable) spécifiques à OpenGL sont OpenGL32.lib et glu32.lib ainsi que glut32.lib si GLUT est utilisé.
- Les dll (nécessaires à l'exécution) spécifiques à OpenGL sont OpenGL32.dll et glu32.dll ainsi que glut32.dll si GLUT est utilisé.
Si Visual Studio 2010 sous Windows est installé, l'utilisation des fichiers contenus dans l'archive IG.zip peut être nécessaire. Cette archive contient un répertoire "Include" contenant les fichiers .h d'OpenGL, un répertoire "Lib" contenant les fichiers .lib d'OpenGL en version Microsoft (ms) et Mesa3D (mesa) ainsi que la dll glut32.dll nécessaire à l'exécution d'un programme 32 bits utilisant la librairie GLUT (les autres dll OpenGL sont préinstallées dans le système d'exploitation).
Si gcc sous Linux est utilisé, Mesa3D devrait avoir été installé au cours de l'installation
des outils de développement (gcc). S'il ne l'est pas, ou si l'on constate l'absence de GLUT, ou si l'on souhaite
utiliser une version plus récente que celle disponible (en septembre 2009, la version la plus récente disponible
de Mesa3D est la version 7.5.1 qui est compatible OpenGL 2.1), il sera nécessaire de
télécharger et d'installer (compilation puis installation, une archive pour OpenGL, une archive pour
GLUT et une archive pour des exemples) la version souhaitée.
Pour l'édition de lien d'un exécutable OpenGL & GLUT, il est nécessaire de spécifier les
librairies GL, GLU et glut dans la ligne de commande de compilation.
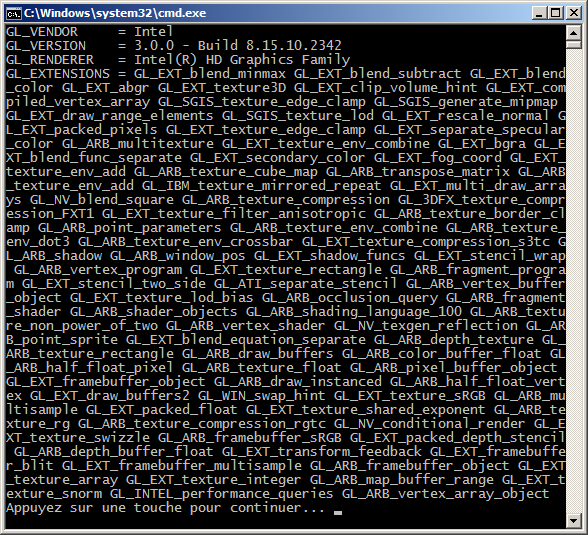
a) Télécharger le programme source exemple suivant : GetConfig2011-2012.cpp.
Ce programme a pour but d'initialiser OpenGL pour en extraire et afficher les informations de version.
Réaliser en la compilation et l'exécution.
| Création d'une solution Visual Studio Création et configuration d'un projet |
| (1) Extraire l'archive IG.zip dans le répertoire personnel. Noter la localisation des répertoires include et lib qui contiennent respectivement les fichiers d'inclusion spécifiques à OpenGL (compilation) et les librairies spécifiques à OpenGL (édition de liens). Noter la présence d'une dll (Glut32.dll). |
| (2) Créer un projet. Aucune solution n'existant, la création du projet s'accompagnera de la création
de la solution le contenant. Sauvegarder la solution et le projet dans le répertoire IG créé lors de l'extraction de l'archive. Le projet créé doit être de type "Application Console Win32", "Sans entête précompilé" et "Projet vide". |
| (3) Ajouter le fichier source à compiler dans la liste des fichiers source du projet. |
| Compilation impossible car les fichiers d'entête OpenGL sont introuvables. |
| (4) Demander les propriétés du projet et configurer un répertoire include supplémentaire dans les options de compilation. Indiquer le répertoire include des entêtes OpenGL. |
| Compilation réussie mais erreur lors de l'édition de liens car la librarie glut32.lib est préconfigurée pour être utilisée. |
| (5) Demander les propriétés du projet et configurer l'exclusion du fichier Glut32.lib des librairies implicites utilisées lors de l'édition de liens (options d'éditions de liens). |
| (6) Ajouter le fichier librairie Glut32.ms.lib à la liste des fichiers du projet. |
| Edition de liens réussie mais erreur à l'exécution car la dll glut32.dll est introuvable. |
| (7) Repérer le répertoire qui contient l'exécutable créé et y copier la dll glut32.dll. |
| (8) Exécuter. |
| (9) Suggestion: (a) Créer un répertoire "Bin" dans le répertoire IG. (b) Y copier la dll Glut32.dll (c) Configurer une opération post-built dans les propriétés du projet pour copier dans ce répertoire l'exécutable créé. (d) Faire l'opération (c) pour tous les projets de manière à ce que tous les exécutables créés en TP y soient copiés. |
b) Recommencer la procédure de test avec le fichier source suivant:
Animation2011-2012.cpp.
Ce programme utilise OpenGL et GLUt pour afficher une scène 3D simple avec animation automatique, matériel
et lumières, caméra de visualisation en projection en perspective, ...
Cet exemple pourra être utilisé pour les TPs suivants comme base de travail et être adapté à
l'affichage d'autres scènes.


Suggestion: Déterminer une méthode permettant de dupliquer un projet Visual Studio.
c) Recommencer la procédure de test avec le fichier source suivant:
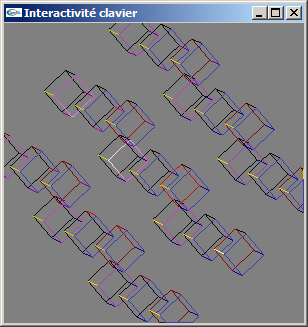
Interactivite2011-2012.cpp.
Ce programme utilise OpenGL et GLUt pour afficher une scène 3D simple avec animation au clavier, matériel
et lumières, caméra de visualisation en projection parallèle orthographique, ...
Cet exemple pourra être utilisé pour les TPs suivants comme base de travail et être adapté à l'affichage
d'autres scènes.



![]()
TD n°4 : Caméras en OpenGL
Exercice n°1
a) On considère une scène quelconque occupant un volume sphérique de rayon r centré sur le point de coordonnées (10.0, 20.0, 0.0). On souhaite la visualiser en projection parallèle orthographique selon l'axe -z. Définir quels paramètres seront passés à la fonction glOrtho pour modéliser une telle caméra.
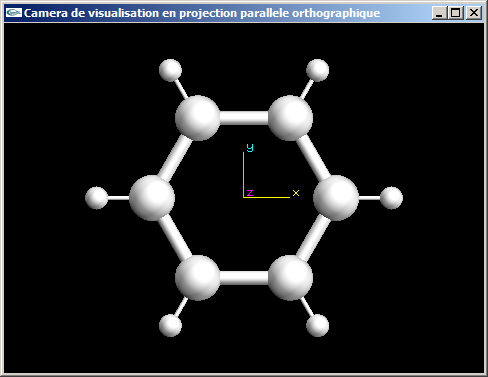
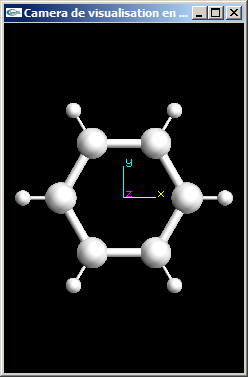
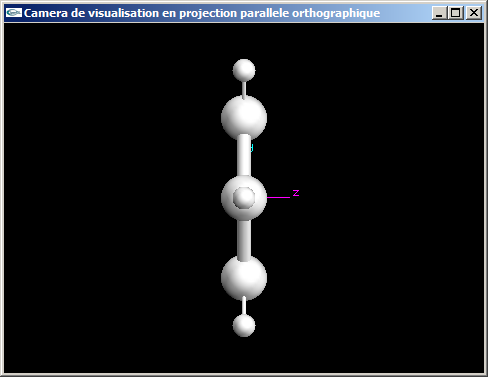
b) On souhaite maintenant visualiser cette même scène toujours en projection parallèle orthographique, mais selon l'axe x. Quelles modifications sont à apporter au code de définition de la caméra de la question (a) pour obtenir ce nouveau point de vue?
Exercice n°2
a) La fonction gluPerspective prend comme paramètre un angle d'ouverture vertical qu'il s'agit ici de déterminer.
On considère une scène quelconque occupant un volume sphérique de rayon r. Le centre de cette scène,
en direction duquel la caméra est orientée, est situé à une distance d de la caméra de
visualisation. On suppose d > r.
Evaluer l'angle d'ouverture vertical à utiliser pour assurer une vue entière de la scène dans la fenêtre
de visualisation.
b) A quelles valeurs définir les paramètres cmin et cmax de gluPerspective pour être certain que la scène ne sera pas découpée en z?
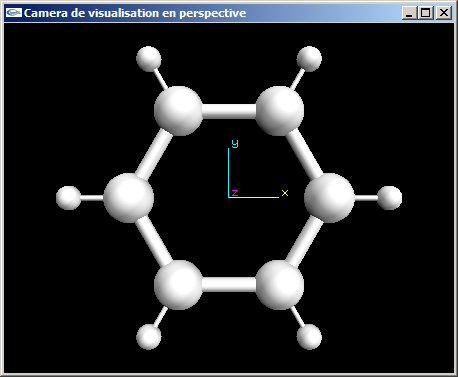
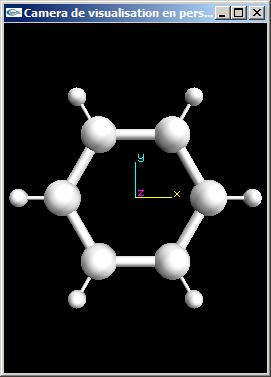
c) Application numérique:
- La scène a pour rayon 10.0.
- Elle est placée centrée en position (30.0, 20.0, -10.0).
- La caméra est placée en position (-20.0, 10.0, 30.0).
d) Quels sont les paramètres de gluLookAt correspondant à la question précédente?
e) Programmer le bloc de code OpenGL modélisant la caméra de visualisation telle que définie dans les questions précédentes.
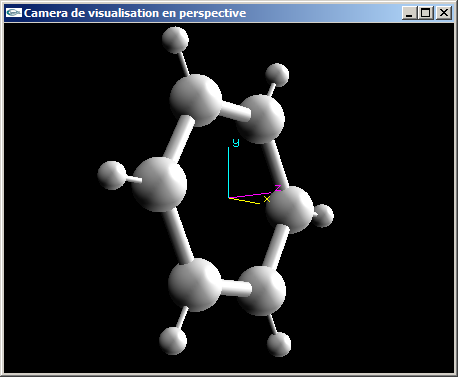
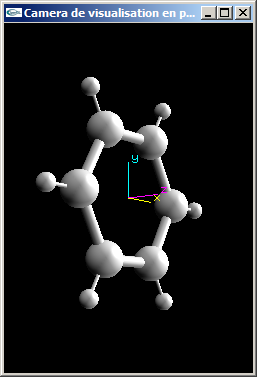
Solutions
| Exercice n°1 question (a) | ||
| Exercice n°1 question (b) | ||
| Exercice n°2 question (b) | ||
| Exercice n°2 question (e) |
![]()
TP n°2 : Primitives graphiques et caméras OpenGL
GLUT: Construction de l'interface utilisateur d'un programme affichant de l'OpenGL.
Fonctions de paramètrage et de création d'une fenêtre d'affichage.
Modèle de programmation événementiel -> Définition de fonctions à exécuter en réaction aux divers événements pouvant arriver au cours de la vie du programme:
- Fonction "display": rafraîchissement de la fenêtre d'affichage
- Fonction "reshape": modification de la taille de la fenêtre d'affichage
- Fonction "keyboard": utilisation d'une touche du clavier possédant un code ASCII
- Fonction "special": utilisation d'une touche special du clavier (touche de fonction, touche de curseur, ...)
Exercice n°1
Implanter le bras robot partiel du TD n°2 avec segments modélisés par des cylindres
tels qu'implantés au TD n°3.
On utilisera comme base le fichier source de la question c) du TP n°1 et on réécrira la fonction
scene.
On adaptera aussi les contrôles clavier pour rendre possible la modification des angles r1 et r2 au moyen des
touches de curseur.
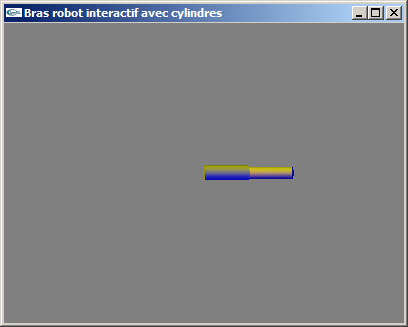
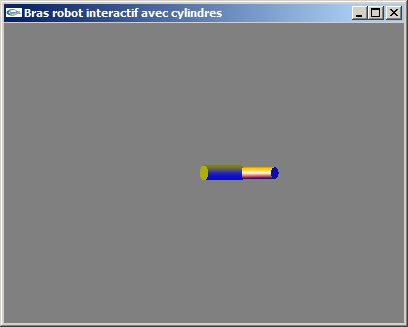
Solutions
| Exercice n°1 |
![]()
TD n°5 : Matériaux et lumières en OpenGL
On considère une scène quelconque centrée sur l'origine, occupant un volume sphérique de rayon 10.0 et modélisée dans un repère où xz est le plan de l'horizontale et y est l'axe de la verticale. On souhaite tester différents scénarii d'éclairage et de gestion de matériel sur cette scène. Dans un premier temps, le matériel utilisé est uniquement diffusant selon les coefficients (0.8, 0.8, 0.8) sans réflexion spéculaire.
a) Définir une lumière ponctuelle jaune placée à l'origine éclairant cette scène.
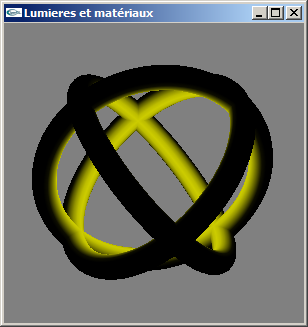
b) Ajouter une lumière directionnelle cyan provenant de la droite.
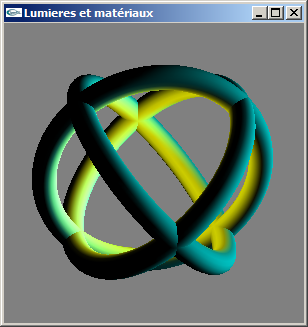
c) Ajouter une lumière spot magenta placée en position (-20.0, 20.0, 20.0), orientée en direction de l'origine et ouverte de 20.0°.
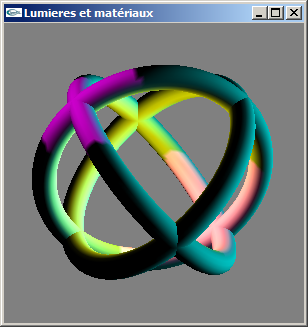
d) Modifier les trois lumières pour qu'elles intègrent la génération de réflexions spéculaires blanches. Modifier le matériel pour qu'il réponde dans le blanc à des éclairages en lumière spéculaire.
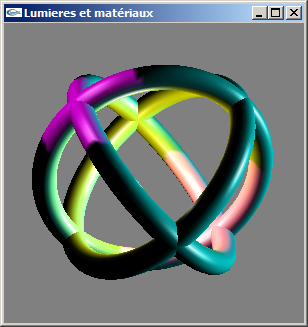
e) Modifier les éclairages pour ne plus gérer qu'une seule lumière ambiante jaune moyen et ajouter une réponse ambiante de coefficients (0.2, 0.2, 0.2) pour le matériel.

Solutions
| Exercice n°1 |
![]()
TP n°3 : Caméras en OpenGL, animation automatique
Exercice n°1
a) Adapter la caméra virtuelle de l'exercice n°1 du TP n°2 pour la transformer
en une caméra de visualisation en perspective définie selon les caractéristiques suivantes:
Elle est placée en position (0.0, 10.0, 20.0) dans le repère de modélisation. Elle est orientée
en direction de l'origine du repère de modélisation. Son axe vertical est l'axe (0.0, 1.0, 0.0) du repère
de modélisation. Elle possède un angle d'ouverture vertical de 16°. Elle conserve le ratio fenêtre.
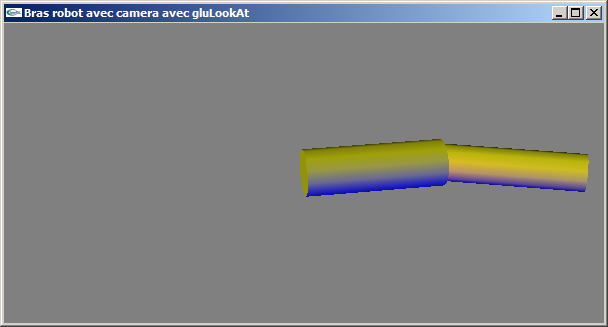
b) L'utilisation de la fonction gluLookAt est interdite. Modifier le programme de la question (a) pour utiliser une rotation et une translation à la place.

Exercice n°2
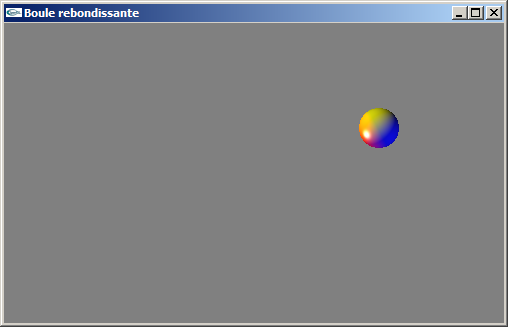
On considère une sphère de 20 pixels de rayon placée au centre d'une fenêtre d'affichage de 500 pixels de large et 300 pixels de haut. Cette sphère se déplace dans la fenêtre et rebondit sur ses bords. Elle se déplace "en diagonal" à raison de +/- 1 pixel en x et en y entre chaque image.
a) Implanter l'application OpenGL + GLUT réalisant cette animation. On s'attachera à définir correctement la caméra virtuelle de visualisation et à implanter l'animation au moyen d'une fonction idle.
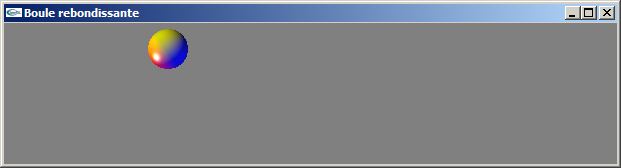
b) Adapter le programme de la question (a) pour que la sphère ne risque pas de disparaitre en cas de redimensionnement de la fenêtre d'affichage. Si elle reste dans la fenêtre, elle n'est pas modifiée. Si elle n'y reste pas, elle est replacée sur le bord qu'elle a rencontré au cours de l'opération de redimensionnement.
Solutions
| Exercice n°1 question (a) | ||
| Exercice n°1 question (b) version 1 | ||
| Exercice n°1 question (b) version 2 | ||
| Exercice n°2 question (a) | ||
| Exercice n°2 question (b) |
![]()
Exercice n°1
Le TD est à réaliser en langage C++.
a) Implanter une classe mère de modélisation de coordonnées homogènes 3D.
b) Dériver de la classe de la question (a) une classe position en coordonnées homogènes 3D.
c) Dériver de la classe de la question (a) une classe direction en coordonnées homogènes 3D.
d) Implanter une méthode de calcul de la distance entre deux positions.
e) Implanter une méthode de calcul de la norme d'une direction.
f) Implanter une méthode de normalisation d'une direction.
g) Implanter une méthode de calcul du produit scalaire entre deux directions.
h) Implanter une méthode de calcul du produit vectoriel entre deux directions.
Solutions
| CoordonneesHomogenes.h |
| CoordonneesHomogenes.cpp |
| Position3D.h |
| Position3D.cpp |
| Direction3D.h |
| Direction3D.cpp |
| Mathématiques de l'Infographie |
![]()
TP n°4 : Matériaux et lumières en OpenGL
Exercice n°1
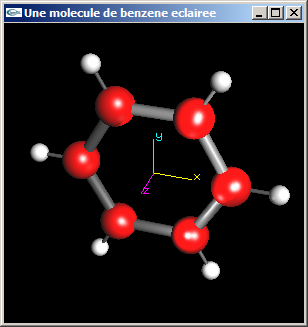
Le fichier suivant contient une application de modélisation de la molécule de benzène du TD n°4: MoleculeBenzene.cpp. Sa compilation nécessite l'utilisation de la librairie Modules2011-2012.lib et des fichiers d'entête ModuleAxes.h et ModuleMatriceVecteur.h. Cette application OpenGL ne comporte aucune instruction permettant de gérer les matériaux et les lumières.
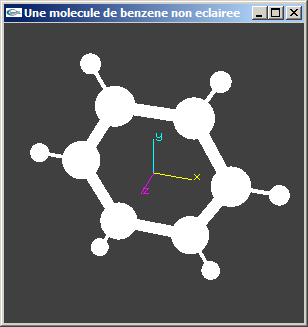
| Une molécule de benzène non éclairée |
a) Placer une lumière ponctuelle en position (1.0, -1.0, 1.0). Lui donner la couleur jaune en diffusion et blanche en spéculaire. Activer l'utilisation de cette lumière.
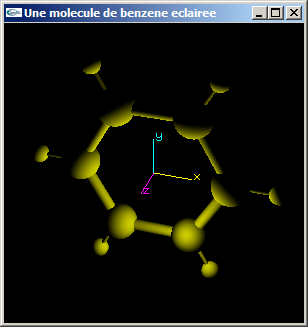
b) Modifier la lumière de la question (a) pour implanter une décroissance quadratique de l'éclairage avec la distance à la source lumineuse.
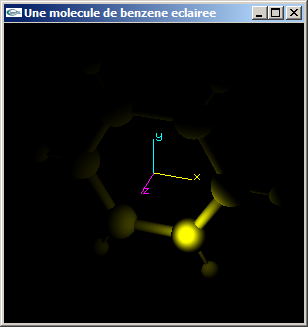
c) Modifier le programme obtenu à l'issue de la question (b) pour pouvoir activer/désactiver au clavier la lumière ponctuelle. Ajouter une seconde lumière directionnelle définie selon les caractéristiques suivantes:
- Sa direction d'incidence est (-1.0, -1.0, -1.0).
- Elle est de couleur cyan en diffusion.
- Elle est de couleur blanche en spéculaire.
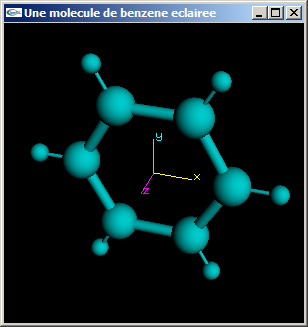
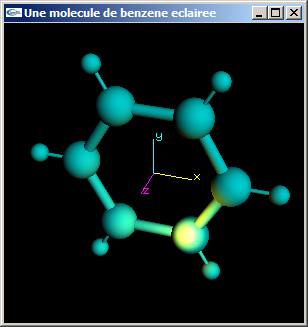
Lumière directionnelle seule - Lumières directionnelle et ponctuelle combinées
d) Modifier le programme obtenu à l'issue de la question (c) pour pouvoir activer/désactiver au clavier les deux lumières. Ajouter une troisième lumière de type spot définie selon les caractéristiques suivantes:
- Sa position est (4.0, 3.0, 5.0).
- Elle est orientée vers le point de coordonnées (1.0, 1.0, 0.0).
- Son ouverture totale est de 30.0°.
- Elle est de couleur magenta en diffusion.
- Elle est de couleur blanche en spéculaire.

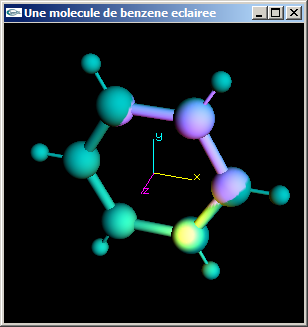
e) Modifier le programme obtenu à l'issue de la question (d) pour pouvoir activer/désactiver au clavier les trois lumières. Ajouter une quatrième lumière ambiante de couleur gris moyen (0.5, 0.5, 0.5).
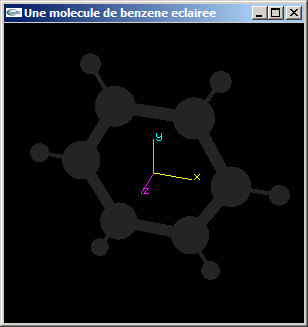
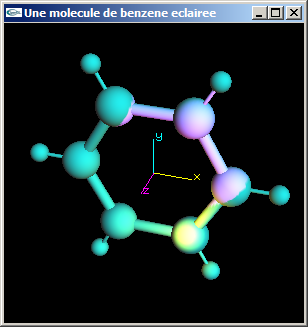
Lumière ambiante seule - Lumières ponctuelle, directionnelle, spot et ambiante combinées
f) Modifier le programme obtenu à la question (e) pour que les 4 lumières soient actives et que les objets de la scène soient affectés de matériaux tels que:
- Les liaisons soient de couleur gris foncé en diffusion et blanches en spéculaire.
- Les atomes de carbone (grosses sphères) soient de couleur rouge en diffusion et blanches en spéculaire.
- Les atome d'hydrogène (petites sphères) soient de couleur blanche en diffusion et blanches en spéculaire.
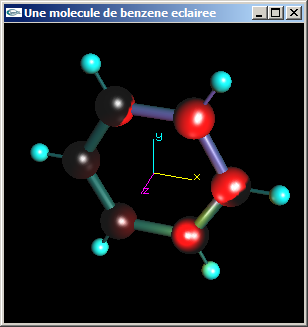
Pour vérifier que les couleurs sont bonnes, on pourra modifier les lumières pour qu'elles deviennent intégralement blanches.
Solutions
![]()
Exercice n°1
On donne les fichiers d'entête suivants:
a) Développer le constructeur sans paramètre de la classe TransformationGeometrique. Ce constructeur initialise this avec la transformation identité.
b) Développer la méthode transforme de la classe TransformationGeometrique permettant de transformer un objet CoordonneesHomogenes (voir TD n°6) par la transformation géométrique représentée par this. Le résultat obtenu par transformation est stocké dans l'objet CoordonneesHomogenes.
c) Développer la méthode produit de la classe TransformationGeometrique permettant de calculer le produit des deux objets TransformationGeometrique passés en paramètre et stockant le résultat dans this.
d) Développer le constructeur à trois paramètres double de la classe Translation.
e) Développer le constructeur à quatre paramètres double de la classe Rotation (angle en degrés, axe pas obligatoirement normé).
Exercice n°2
Proposer une méthode permettant de tester le parallélisme de 2 facettes triangulaires.
Solutions (avec utilisation du TD n°6)
| TransformationGeometrique.cpp |
| Translation.cpp |
| Rotation.cpp |
| TransformationGeometrique.h |
| Translation.h |
| Rotation.h |
| Mathématiques de l'Infographie |
![]()
Exercice n°1
On souhaite implanter la transformation géométrique permettant de transformer des coordonnées de modélisation en coordonnées observateur. On souhaite pouvoir utiliser comme paramètres la position de l'observateur et la position du point visé tout en conservant l'axe y vertical (voir chapitre "Visualisation").
a) Développer le fichier d'entête d'une classe dérivant de TransformationGeometrique comportant les méthodes nécessaires à ce travail.
b) Implanter cette classe au sein du fichier .cpp correspondant.
c) Tester cette classe. On pourra par exemple s'en servir pour transformer les coordonnées des 8 sommets d'un cube et se servir des coordonnées observateur obtenues pour afficher le cube en fil de fer.
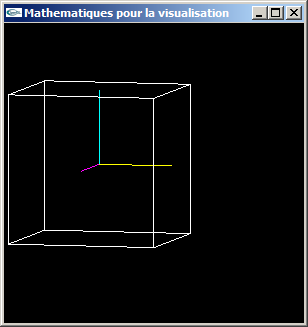
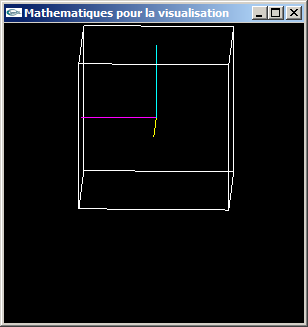
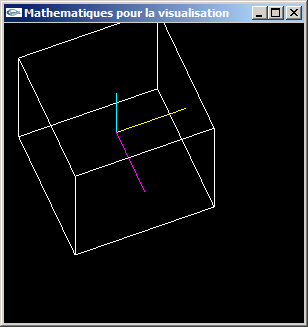
Parallèles conservées
Axe x en jaune, axe y en cyan, axe z en magenta
d) Implanter un nouveau fichier .h ainsi que le fichier .cpp qui lui correspond pour permettre le passage en coordonnées écran avec mise en perspective à partir de coordonnées globales.
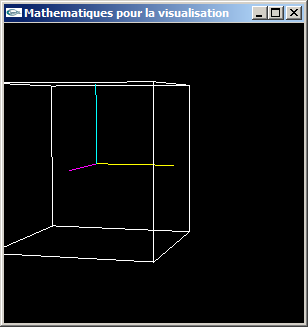
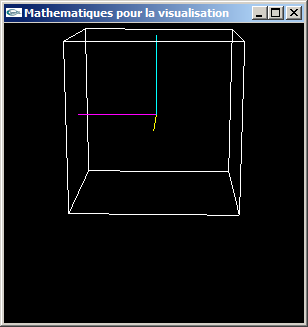
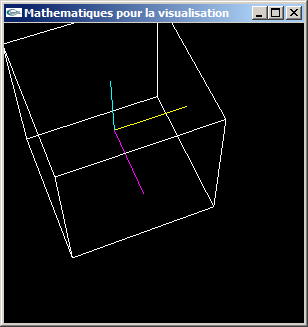
Vue éloignée: Déformations peu prononcées
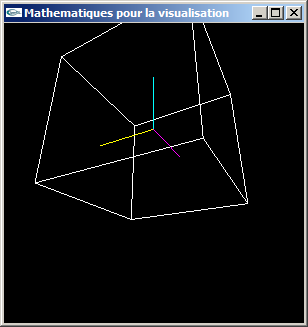
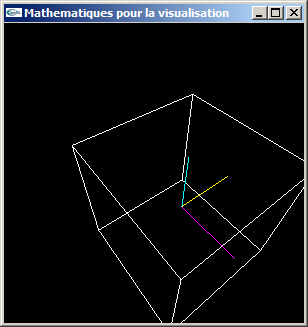
Vue rapprochée: Déformations importantes
Solutions (avec utilisation des TD n°6 et n°7)
| ProjectionParalleleOrthographique.h |
| ProjectionParalleleOrthographique.cpp |
| ProjectionPerspective.h |
| ProjectionPerspective.cpp |
| Mathématiques pour la visualisation |
![]()
On pourra s'aider du document de référence de description de GLUt disponible à l'URL suivante: Spécifications de GLUT version 3
Exercice n°1
a) Développer un programme C+OpenGL+GLUt affichant une scène composée d'une sphère d'exactement
10 pixels de rayon au centre de la fenêtre de visualisation. L'affichage se
fera en projection parallèle orthographique.
Suggestion: Paramétrer la caméra pour qu'elle compte en pixels.
b) Modifier le programme de la question (a) pour que la souris soit utilisable de manière que, lorsque l'utilisateur clique dans la fenêtre d'affichage avec le bouton gauche, la sphère rejoigne instantanément la position cliquée.
c) Modifier le programme de la question (b) pour que la souris soit utilisable de manière que, lorsque l'utilisateur clique dans la fenêtre d'affichage avec le bouton droit, la sphère rejoigne instantanément la position cliquée et se déplace avec les mouvements de la souris tant que le bouton reste appuyé.
Exercice n°2
Le but de cet exercice est de rendre possible la "manipulation" à l'écran d'un objet.
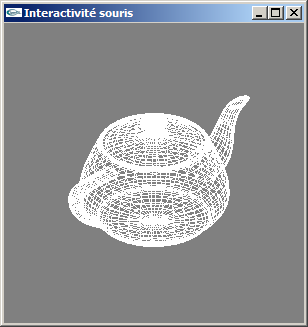
a) Développer un programme d'affichage d'un teapot.
Il sera affiché en gros plan. Le type de caméra n'a pas d'importance.

b) Implanter l'utilisation de la souris pour que le teapot soit manipulable (i.e. qu'il puisse subir des rotations) au
moyen du bouton droit en corrélation avec les déplacements de la souris.
Les déplacements de souris de haut en bas et de bas en haut auront pour conséquence une rotation autour de
l'axe x. Les déplacements de droite à gauche et de gauche à droite auront pour conséquence une
rotation autour de l'axe y.
Solutions
![]()
a) Définir les classes Position2D, Rectangle2D et Segment2D utilisées pour l'implantation du clipping de segments 2D dans des rectangles 2D à bords parallèles aux axes selon la technique de Cohen-Sutherland.
b) Implanter une méthode de calcul du code de Cohen-Sutherland définissant la position d'une Position2D vis à vis d'un Rectangle2D.
c) Implanter une méthode de calcul de l'ordonnée de l'intersection entre la droite soustendue par un Segment2D et une droite verticale.
d) Implanter une méthode de calcul de l'abscisse de l'intersection entre la droite soustendue par un Segment2D et une droite horizontale.
e) Implanter une méthode permettant de clipper un segment2D à l'intérieur d'un Rectangle2D.

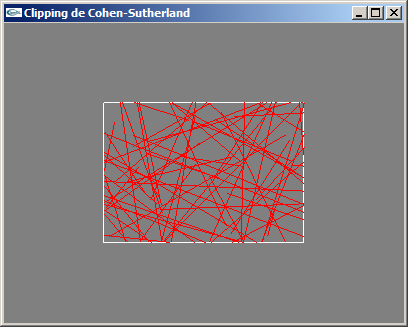
Solutions
| Clipping de Cohen-Sutherland |
![]()
On donne les trois classes Position2D, Segment2D et Rectangle2D définies par les fichiers suivants:
| Position2D.h |
| Position2D.cpp |
| Segment2D.h |
| Segment2D.cpp |
| Rectangle2D.h |
| Rectangle2D.cpp |
Implanter et valider l'algorithme de Cohen-Sutherland tel que défini au TD n°8.


Solutions
| Clipping de Cohen-Sutherland |
![]()
TP n°8 : Le plaçage de texture
Le plaçage de texture est une technique qui vise à créer des détails de surface sur les objets en les recouvrant d'une
image.
L'avantage est que les détails n'ont alors pas à être créés géométriquement.
Les inconvénients sont:
- qu'il faut disposer d'une image de la surface,
- qu'il faut contrôler le processus de recouvrement de l'objet (positionnement de l'image, agrandissement/réduction,
...),
- qu'il est un peu plus lent d'afficher avec plaçage de texture que sans plaçage.
OpenGL ne comporte aucune fonction permettant d'importer une image.
-> Il faut faire appel à des librairies tièrces pour utiliser des images png, gif, jpg, ...
OpenGL comporte les fonctions qui vont permettre de paramétrer et de contrôler le processus de plaçage de texture.
Les opérations à mettre en oeuvre sont les suivantes:
- Importation de l'image
- Transmission de l'image au dispositif OpenGL
- Paramètrage de la méthode de plaçage
- Activation de l'utilisation d'une texture
- Lors de la création d'un primitive graphique, avant chaque spécification de la position d'un vertex dans
le repère de modélisation, spécification de sa position dans image placée.
Exercice n°1
Importer et compiler le fichier source: PlacageTextureSurCarre.cpp.
Importer l'image Damier.raw dans le répertoire qui contient l'exécutable généré ci-dessus.
Cette image est au format raw pour 16x16 pixels. Elle sera lue par l'exécutable et utilisée comme image à placer.

Exercice n°2
En s'inspirant de l'exercice n°1, développer une fonction permettant de texturer les 6 faces d'un cube.

On pourra utiliser la fonction de modélisation d'un cube suivante et lui ajouter le code manquant:
void mySolidCube(float c){
c /= 2.0F;
GLboolean nm = glIsEnabled(GL_NORMALIZE);
if ( !nm )
glEnable(GL_NORMALIZE);
float normale[4];
glGetFloatv(GL_CURRENT_NORMAL,normale);
glPushMatrix();
glBegin(GL_QUADS);
{ glNormal3f(0.0F,0.0F,-1.0F);
glVertex3f( c, c,-c);
glVertex3f( c,-c,-c);
glVertex3f(-c,-c,-c);
glVertex3f(-c, c,-c); }
{ glNormal3f(0.0F,0.0F,1.0F);
glVertex3f( c, c, c);
glVertex3f(-c, c, c);
glVertex3f(-c,-c, c);
glVertex3f( c,-c, c); }
{ glNormal3f(-1.0F,0.0F,0.0F);
glVertex3f(-c, c,-c);
glVertex3f(-c,-c,-c);
glVertex3f(-c,-c, c);
glVertex3f(-c, c, c); }
{ glNormal3f(1.0F,0.0F,0.0F);
glVertex3f( c, c, c);
glVertex3f( c,-c, c);
glVertex3f( c,-c,-c);
glVertex3f( c, c,-c); }
{ glNormal3f(0.0F,-1.0F,0.0F);
glVertex3f(-c,-c, c);
glVertex3f(-c,-c,-c);
glVertex3f( c,-c,-c);
glVertex3f( c,-c, c); }
{ glNormal3f(0.0F,1.0F,0.0F);
glVertex3f( c, c, c);
glVertex3f( c, c,-c);
glVertex3f(-c, c,-c);
glVertex3f(-c, c, c); }
glEnd();
glPopMatrix();
glNormal3f(normale[0],normale[1],normale[2]);
if ( !nm )
glDisable(GL_NORMALIZE);
}
Exercice n°3
Développer une fonction permettant de texturer un cylindre.
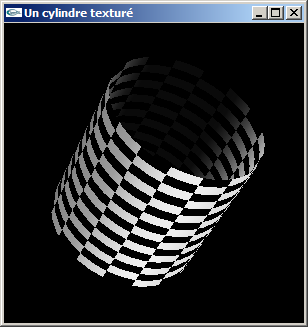
On pourra s'inspirer de la fonction ci-dessous en lui ajoutant le code manquant nécessaire au texturage:
void mySolidCylinder(float hauteur,float rayon,int ns,int
nl) {
GLboolean nm = glIsEnabled(GL_NORMALIZE);
if ( !nm )
glEnable(GL_NORMALIZE);
float normale[4];
glGetFloatv(GL_CURRENT_NORMAL,normale);
glPushMatrix();
for ( int j = 0 ; j < nl ; j++ ) {
float hi = hauteur/2-j*hauteur/nl;
float hf = hi-hauteur/nl;
glBegin(GL_QUAD_STRIP);
for( int i = 0 ; i <= ns ; i++ ) {
float a = (2*M_PI*i)/ns;
float cs = cos(a);
float sn = -sin(a);
glNormal3f(cs,0.0F,sn);
float x = rayon*cs;
float z = rayon*sn;
glVertex3f(x,hi,z);
glVertex3f(x,hf,z); }
glEnd(); }
glPopMatrix();
glNormal3f(normale[0],normale[1],normale[2]);
if ( !nm )
glDisable(GL_NORMALIZE);
}
Cette fonction modélise un cylindre orienté en y selon les valeurs de hauteur et de rayon passées en paramètre, en facettisant en ns sections autour de l'axe y et nl sections le long de l'axe y.
Solutions
![]()
TD n°9 : Calcul des rayons réfléchi et transmis pour le lancer de rayons, test d'intersection pour le lancer de rayons
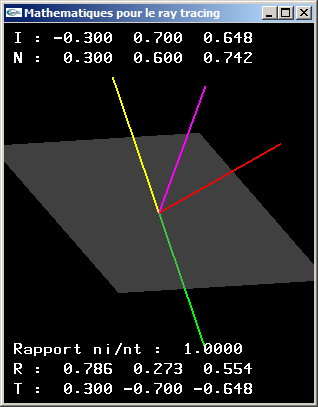
a) La formule suivante permet le calcul du rayon réfléchi sur une interface au niveau d'un point d'incidence:

Le vecteur
 est la direction normée du rayon incident. Le vecteur
est la direction normée du rayon incident. Le vecteur
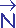 est la normale à l'interface au point d'incidence.
est la normale à l'interface au point d'incidence.
Implanter cette formule.
b) La formule suivante permet le calcul du rayon transmis à travers une interface au niveau d'un point d'incidence:

Le vecteur
 est la direction normée du rayon incident. Le vecteur
est la direction normée du rayon incident. Le vecteur
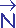 est la normale à l'interface au point d'incidence. n est le rapport ni/nt entre les coefficients de réfraction des
milieux d'incidence et de transmission.
est la normale à l'interface au point d'incidence. n est le rapport ni/nt entre les coefficients de réfraction des
milieux d'incidence et de transmission.
Implanter cette formule.
c) Définir une classe sphère.
d) Définir une classe rayon.
e) Implanter une méthode de test de l'existence d'une intersection entre un rayon et une sphère.
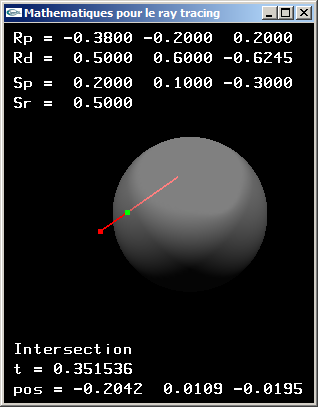
Solutions
![]()
TD n°10 : Les courbes de Bézier
La formule suivante permet le calcul le la courbe de Bézier C(t) définie sur les n+1 sommets P numérotés de 0 à n:
 pour t compris dans l'intervalle [0.0,1.0]
pour t compris dans l'intervalle [0.0,1.0]
a) Développer une fonction factoriel(int n).
b) Développer une fonction C(int i,int n).
c) Développer une fonction de calcul de la courbe de Bézier définie sur m points 3D à partir d'une ligne polygonale de n+1 points 3D.
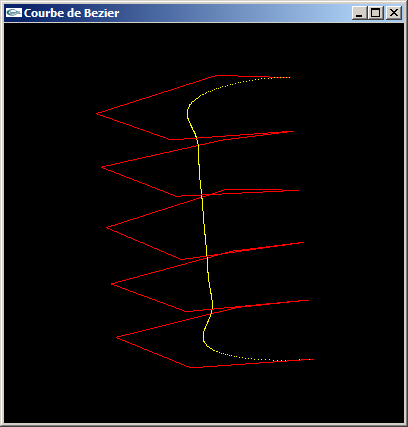
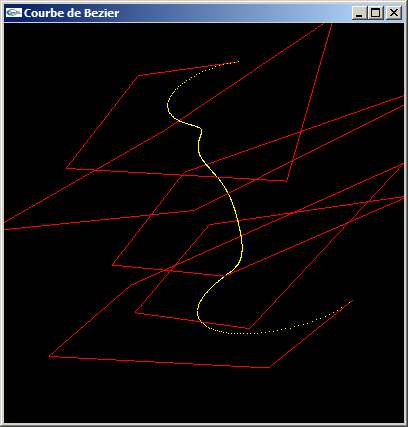
Solutions
![]()
TP n°9 : Les courbes de Bézier
Réaliser l'implantation du calcul de courbe de Bézier.
Tester sur la série de 21 sommets suivante pour la génération d'une courbe de 500 sommets avec affichage graphique
en utilisant OpenGL:
( 5.0, -10.0, 5.0)
(-5.0, -9.1, 5.0)
(-5.0, -7.8, -5.0)
( 5.0, -7.2, -5.0)
( 5.0, -5.8, 5.0)
(-5.0, -5.1, 5.0)
(-5.0, -4.0, -5.0)
( 5.0, -3.2, -5.0)
( 5.0, -1.7, 5.0)
(-5.0, -1.4, 5.0)
(-5.0, 0.0, -5.0)
( 5.0, 1.2, -5.0)
( 5.0, 2.0, 5.0)
(-5.0, 3.1, 5.0)
(-5.0, 4.3, -5.0)
( 5.0, 4.7, -5.0)
( 5.0, 6.2, 5.0)
(-5.0, 7.1, 5.0)
(-5.0, 8.1, -5.0)
( 5.0, 9.3, -5.0)
( 5.0, 10.0, 5.0)


Solutions
![]()