0. Problématique
L'affichage d'une scène 3D nécessite que soit respectée la règle qui veut que, si un objet A est situé devant l'objet B du point de vue
de l'observateur, celui-ci verra l'objet A et la seule partie de l'objet B, si elle existe, qui n'est pas derrière l'objet A.
Les algorithmes qui permettent de s'assurer de cet état de fait sont nommés "Algorithmes d'élimination des parties cachées".
De nombreux algorithmes d'élimination des parties cachées ont été développés au cours du temps :
- algorithme du Z-Buffer,
- algorithme du peintre,
- algorithmes de la ligne de balayage (scanline, ...),
- algorithmes par subdivision de l'image (Warnock, ...),
- ray casting,
- ...
L'existence de ce grand nombre de techniques correspond pour partie à l'existence passée ou encore actuelle de contraintes de puissance de
calcul, et aussi à l'existence de situations particulières qui font que l'utilisation de tel ou tel algorithme sera avantageuse si on est
dans une de ces situations.
Un bon exemple est l'algorithme du peintre qui consiste à obtenir l'image en dessinant entièrement les objets les uns sur les autres du plus
profond au moins profond. Cet algorithme est particulièrement intéressant si l'ordre de profondeur des objets existe et est implicitement connu
et donc si aucun tri n'a à être effectivement réalisé. Si on n'est pas dans cette situation, il sera soit impossible à utiliser (impossible
de trier par exemple parce que les objets se coupent les uns les autres), soit inintéressant si le nombre d'objets à afficher et donc à trier
est grand (temps non linaire des algorithmes de tri en fonction de la taille de l'ensemble à trier).
La suite de ce chapitre s'attache à l'algorithme du Z-Buffer qui est historiquement associé à OpenGL.
1. Introduction
Lors de la visualisation d'une scène, l'algorithme du Z-Buffer calcule l'image de manière que l'affichage de tout objet ou morceau d'objet masqué par un autre objet ou par lui même soit supprimé. Son but est de déterminer la couleur que doit adopter chaque pixel de l'image obtenue en la calculant à partir de l'objet visible en ce pixel.
Cet algorithme a été décrit au milieu des années 70 par Wolfgang Straßer ("Schnelle Kurven- und Flächendarstellung auf grafischen Sichtgeräten").
Son mode de fonctionnement permet de s'absoudre de problèmes fréquemment insolubles pour d'autres algorithmes d'élimination des parties
cachées :
- Il fonctionne même si les objets représentés se coupent les uns les autres.
- L'ordre dans lequel les objets à afficher lui sont transmis n'a pas d'incidence sur sa capacité à calculer l'image finale.
En particulier, il n'est pas obligatoire de les trier.
- Quel que soit l'ordre dans lequel les objets sont transmis, l'image finale obtenue est la même.
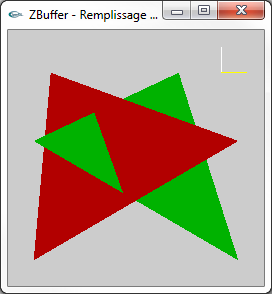
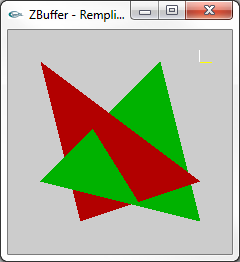
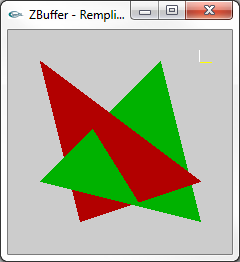
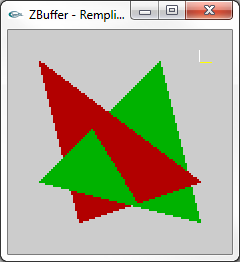
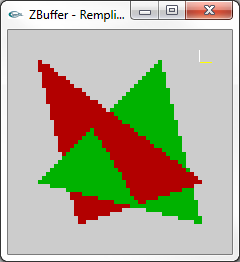
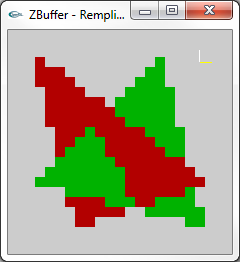
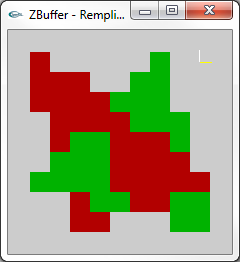
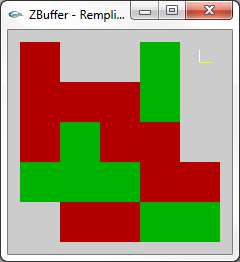
|
Aptitude de l'algorithme du Z-Buffer à accepter des objets |
||||||||
|
||||||||
| Espace pour switcher entre les affichages | ||||||||
2. Principe
Pour chaque pixel de l'image à calculer, une recherche de maximum est effectuée sur les objets de façon à déterminer quel est l'objet qui
est visible en ce pixel et donc quelle est la couleur de ce pixel. Si une image de résolution n sur m pixels doit être obtenue, ce sont n×m
recherches de maximum qui sont donc réalisées permettant in fine de déterminer la couleur des n×m pixels.
En appliquant ce principe, on travaille en faisant une élimination des parties cachées au niveau de chaque pixel. Il n'est donc plus problématique
que les objets se coupent les uns les autres. Il n'y a pas non plus d'ordre de transmission des objets à respecter et donc de tri à réaliser
car le traitement opéré est une recherche de maximum.
Cet algorithme s'appelle Z-Buffer car le traitement qu'il implante utilise des coordonnées écran définies selon le repère généralement utilisé
en informatique graphique : x vers la droite, y vers le haut, z vers l'arrière. C'est donc la coordonnées z qui définit la "distance"
à l'observateur. Plus z est petit plus l'objet est loin de l'observateur. Plus z est grand plus l'objet est proche de l'observateur.
Mise en application
On imagine parfaitement qu'une implantation directe du concept présenté ci-dessus serait problématique en raison de la quantité de calculs qui
serait nécessaire. En effet les résolutions n et m sont couramment de l'ordre de quelques milliers de pixels et les scènes sont couramment constituées
de plusieurs millions d'objets. Effectuer les recherches de maximum indépendamment les unes des autres pour chaque pixel entraînerait des milliards,
voire des centaines de milliards de tests de présence d'un objet en une position écran suivis le cas échéant du calcul de la profondeur de cet
objet en cette position écran suivis le cas échéant du calcul de la couleur de cet objet en cette position écran. On peut compléter l'argument
précédent par la constatation qu'habituellement les objets sont, d'une manière générale, petits à l'écran, et que donc il est probable
qu'une quantité de calcul extrêmement importante sera gaspillée pour faire des tests de présence qui se révèleront négatifs.
Conséquence : L'idée consistant à itérer pour parcourir les pixels de l'image et, pour chacun d'eux, à faire une
recherche de maximum serait une très mauvaise idée si le but est d'obtenir une certaine rapidité de calcul des images.
Une méthode beaucoup plus efficace est la suivante : Le calcul de l’image est effectué séquentiellement en traitant l'ensemble des objets
de la scène les uns à la suite des autres. Le traitement de chaque objet consiste en sa rasterisation pour déterminer l'intégralité des pixels
qui le représenteraient s'il était dessiné seul. Au cours du processus de rasterisation, la "profondeur" écran, c'est à dire le
z écran de l'objet (de -∞, le plus profond possible, à +∞, le moins profond possible) en chaque pixel rasterisé est calculée et est comparée à
celle déjà rencontrée en la position (x,y) du pixel. En fonction du résultat de cette comparaison, la couleur du pixel
est :
- inchangée si la profondeur calculée établit que l'objet en cours de traitement est derrière (profondeur plus
petite),
- affectée avec la couleur de l'objet en cours de traitement en ce pixel, s'il est devant (profondeur plus grande).
On gère ainsi, pour chaque pixel de l'écran, une recherche de maximum dans le but d'afficher finalement l'objet le moins profond
(vis à vis de l'observateur) présent en cette position c'est à dire celui de z maximum.
Calculer une image a pour but de calculer une matrice de couleurs de pixel de résolution nxm (usuellement appelé le tampon couleur, tampon image
ou frame buffer). Un point particulier à l'algorithme du Z-Buffer est que le calcul simultané des z maximum de tous les pixels requière, avant
le lancement du traitement des objets, la réservation d'une matrice de valeurs de résolution nxm pour stocker, en cours de traitement, le z trouvé
en chaque pixel. Un type élémentaire 32 bits (int ou float en C) pour cette matrice assure une précision suffisante pour les recherches de maximum.
Il est fréquent que les algorithmes du Z-Buffer soient conçus pour n'accepter qu'un seul type d'objet : la facette triangulaire. Cette limitation est principalement liée à un objectif de simplification matérielle et d'optimisation. En effet, la rasterisation des facettes triangulaires peut être conduite en utilisant uniquement des entiers et des opérations simples sur ces entiers (voir chapitre algorithmique).
Ne pas réaliser la séquentialisation principale sur les pixels mais sur les objets a beaucoup d'intérêts :
- Une large optimisation des calculs est atteinte de par le fait que l'on ne calcule que des pixels qui appartiennent aux objets et que
l'on ne teste pas tous les pixels de l'image pour chaque objet.
- Il n'y a pas de tri des objets et donc pas de problème de non-linéarité intrinsèque du temps d'exécution. La structure principale
est une boucle simple sur les objets. L'algorithme du Z-Buffer présente donc un temps linéaire du nombre d'objets.
- Il est possible de commencer le calcul de l'image sans connaître l'intégralité de la scène.
- ...
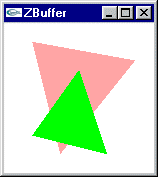
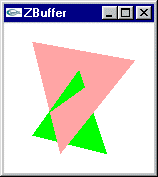
|
Deux facettes à afficher au moyen d’un Z-Buffer |
|
|
3. Implantation
Deux zones mémoire sont réservées. Elles sont de résolutions identiques à la résolution de l'image que l'on souhaite calculer.
On a donc :
- un tampon couleur :
- destiné à contenir la couleur de chacun des pixels de l'image,
- classiquement profond de 24 bits si on travaille en RVB ou de 32 bits en RVBA,
- initialisé à la couleur de fond souhaitée,
- un tampon profondeur :
- destiné à contenir la profondeur écran maximum (le z) de chacun des pixels de l'image,
- classiquement profond de 32 bits (16 ou 24 bits dans le passé),
- initialisé à -∞.
La scène a été pré-traitée et est donc disponible en coordonnées écran c'est à dire en coordonnées comptées en pixels.
On rasterise chaque objet o à afficher en l'ensemble des pixels de coordonnées (x,y) qui le composerait s'il était intégralement
affiché seul.
Au cours de la rasterisation, on calcule la profondeur écran z de chaque pixel de o de coordonnées image (x,y).
Si cette coordonnée z est plus grande que celle déjà présente dans le tampon profondeur aux coordonnées (x,y), la nouvelle profondeur en (x,y) devient
z et la couleur du pixel (x,y) du tampon couleur est réaffectée avec une valeur calculée en fonction de x, de y, des caractéristiques de l'objet
o, de sources lumineuses, ...
Quand tous les objets ont été traités, l'image est disponible dans le tampon couleur pour être affichée à
l'écran.
/* Algorithme du Z-Buffer pour la création d'une image */
réserver et initialiser le tableau prof à -∞
réserver et initialiser le tableau coul à la couleur de fond
pour chaque objet o de la scène à représenter
pour chaque pixel p de coordonnées (x,y) de o
calculer la profondeur z de p
si z > prof[x][y] alors
prof[x][y] = z
coul[x][y] = couleur(o,x,y)
finsi
finpour
finpour
détruire le tableau prof
utiliser le tableau coul puis le détruire
Les objets sont très fréquemment des facettes planes triangulaires car ce sont des surfaces simples à rastériser au moyen de variantes de l'algorithme de Bresenham. De plus, pour ce type d'objet, le calcul de la profondeur écran nécessaire à la rastérisation se marie bien avec l'opération de remplissage et entraîne donc un surcoût de calcul peu important.
Généralement, l'utilisation de l'algorithme du Z-Buffer s'intègre à une boucle d'affichage virtuellement infinie permettant d'enchaîner le calcul et l'affichage d'images. Si la résolution de ces images ne change pas, il n'est pas nécessaire de réaliser la réservation des deux zones mémoire à chaque image. Le gain peut être important car il s'agit là d'une opération longue. Intégré à la boucle infinie d'affichage l'algorithme ci-dessus devient :
/* Algorithme du Z-Buffer pour la création d'une suite */
/* d'images intégrée à la boucle principale d'affichage */
réserver le tableau prof
réserver le tableau coul
tant que ( vrai )
initialiser le tableau prof à -∞
initialiser le tableau coul à la couleur de fond
pour chaque objet o de la scène à représenter
pour chaque pixel p de coordonnées (x,y) de o
calculer la profondeur z de p
Si z > prof[x][y] alors
prof[x][y] = z
coul[x][y] = couleur(o,x,y)
fin si
fin pour
fin pour
utiliser le tableau coul
fin tant que
détruire le tableau prof
détruire le tableau coul
| Z-Buffer sur deux facettes |
|
|
|
Enter pour switcher entre les différents affichage Espace pour switcher entre les modes d'affichage fil de fer et plein b pour switcher entre les affichages sans et avec les triangles réels matérialisés par leurs cotés c pour activer/désactiver l'élimination des parties cachées Touches de curseur et souris pour manipuler la scène |
|
Z-Buffer sur deux facettes avec différentes tailles de pixel virtuel |
|
|
|
Enter pour switcher entre les différents affichage +/ pour augmenter/diminuer la taille des pixels Espace pour switcher entre les modes d'affichage fil de fer et plein b pour switcher entre les affichages sans et avec les triangles réels matérialisés par leurs cotés c pour activer/désactiver l'élimination des parties cachées Touches de curseur et souris pour manipuler la scène |
On dispose d'une facette triangulaire dont les sommets sont connus en coordonnées écran.
Problèmes :
(1) Quels sont les pixels recouvrant cette facette ?
(2) Quelle est la profondeur (le z) de chacun de ces pixels ?
Solution au problème (1) : Implanter un algorithme de remplissage 2D de type "fillPoly" (voir chapitre algorithmique)
Solution au problème (2) : Travailler le remplissage 2D en gérant z en paramètre supplémentaire (pour optimiser les calculs, mariage de la gestion de z avec les variantes d'algorithme de Bresenham utilisés pour de remplissage 2D).
|
Problème (1) : Remplissage d'une facette 2D |
|
|
|
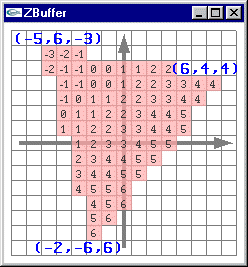
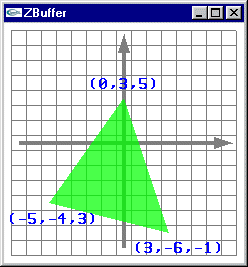
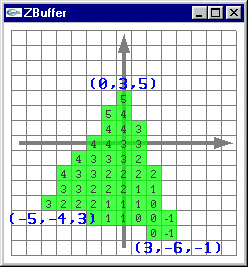
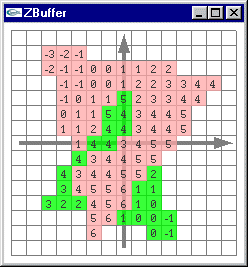
Problème (2) : Remplissage d'une facette 3D |
|
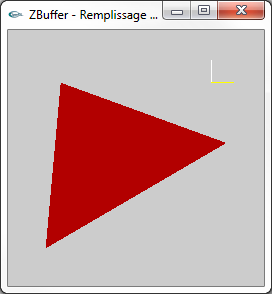
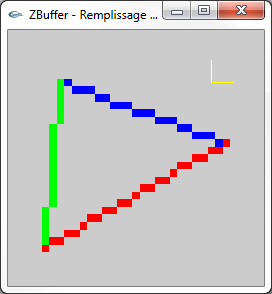
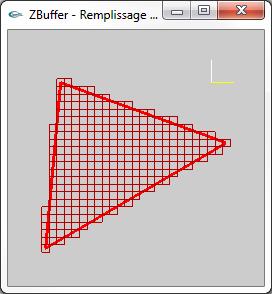
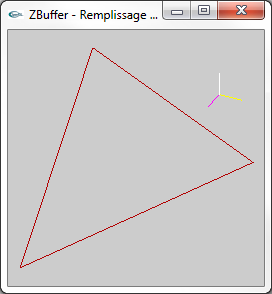
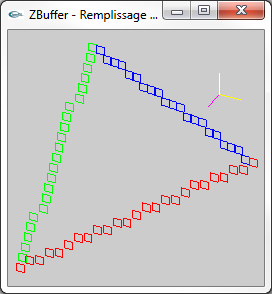
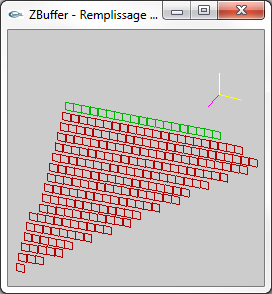
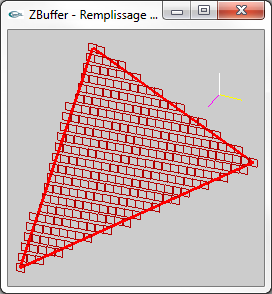
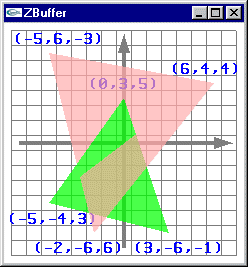
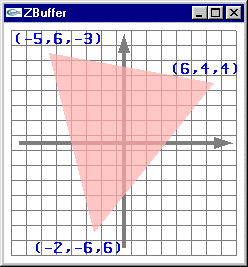
Les images ci-dessous présentent l'affichage des pixels obtenus par rasterisation d'une facette 3D. Pour montrer le placement en 3D virtuelle
des pixels avec un z différent pour chaque pixel, le point de vue adopté n'est pas celui utilisé pour l'affichage véritable c'est à dire
une projection selon l'axe -z qui rend indiscernable la profondeur des différents pixels. Les pixels ressemblent à des tuiles parallèles placées à des z différents de façon régulière. Les trois petits segments jaune, blanc et magenta montrent les axes x, y et z. Le véritable affichage est fait selon l'axe -z. |
|
|
Différentes unités de mesure de performance sont utilisées pour quantifier la rapidité d'une implantation d'un algorithme d'élimination
des parties cachées et plus particulièrement d'une implantation de l'algorithme du Z-Buffer :
- Unités "historiques"
- Segments/seconde
- Polygones/seconde
- Unité actuelle (plus représentative que les unités ci-dessus car indépendante du nombre de pixels moyen des segments et des polygones)
- Taux de génération de pixels (pixels/seconde)
Sur PC, les valeurs caractéristiques sont :
- de quelques centaines de millions à plusieurs centaines de milliards de pixels par seconde,
- de quelques centaines de milliers à plusieurs centaines de millions de polygones par seconde,
pour des cartes graphiques qui coûtent de quelques dizaines d'€ à plusieurs milliers d'€.
Tout comme celles des processeurs, ces performances sont en constante amélioration.
4. Conclusion
L'algorithme du Z-Buffer présente beaucoup d'intérêts :
- Il est facilement implantable. Quelques centaines de lignes de code sont nécessaires.
- Il peut être très optimisé (utilisation exclusive d'entiers et d'opérations élémentaires sur ces entiers, utilisation de
variantes de l'algorithme de Bresenham pour le tracé de segments, ...).
- Il est "facilement" implantable hard.
- Il est "facilement" parallélisable. Un parallélisme sur les données peut être utilisé sur les objets et/ou sur les pixels.
Les cartes graphiques embarquent fréquemment plusieurs milliers de processus graphiques (GPU) fonctionnant en parallèle.
- Il est compatible de manière "simple" avec le calcul d'illumination de Gouraud et le placage de texture (attribution de
valeurs entières supplémentaires de couleur et de coordonnées de texturage aux sommets des facettes triangulaires traitées).
- Il gère implicitement les intersections entre objets.
- Il est caractérisé par des temps d'exécution en O(n) du nombre de facettes et O(n,m) de la résolution des images générées -> bonne
scalabilité.
- Il est suffisamment rapide pour qu'un affichage temps réel puisse être obtenu (plusieurs dizaines voire centaines d'images par seconde)
même sur des scènes complexes et même pour des images haute résolution.
- ...
Rien n'est parfait, il y a aussi des inconvénients :
- La décomposition de chaque surface élémentaire en pixels nécessite une puissance de calcul importante (de l'ordre
de la centaine de Mips pour 100000 facettes/s pour des facettes de 100 pixels de surface moyenne) et une vitesse d'accès mémoire très
élevée. Les cartes graphiques utilisent le parallélisme sur les processeurs pour procurer une puissance de calcul suffisante et des
composants mémoire spécifiques (plus onéreux que la mémoire classique) pour obtenir une bande passante mémoire suffisante.
- Il ne gère pas intrinsèquement les phénomènes de réflexion spéculaire et de transmission. Il ne gère
pas non plus implicitement les ombres portées.
-> Difficultés pour implanter la modélisation de phénomènes optiques complexes pour des rendus
réalistes.
- ...
Pour conclure
L'algorithme du Z-Buffer est devenu l'algorithme standard pour l'obtention en temps réel d'images de qualité moyenne pour des
scènes complexes.
Il est l'algorithme utilisé pour la génération d'images 3D dans les domaines de la conception et fabrication assistée par ordinateur
(station de travail graphique), de la réalité virtuelle, de la réalité augmentée et du jeu où le photoréalisme n'est pas obligatoire.
Il n'est pas utilisé pour la génération d'images photo-réalistes car il est trop limité fonctionnellement du point
de vue des effets qu'il permet de rendre.
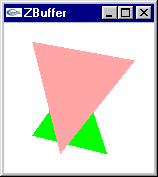
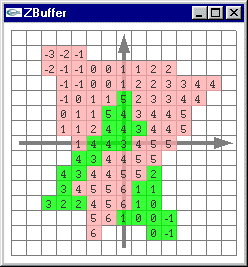 Résultat obtenu pour le calcul
Résultat obtenu pour le calcul