Algorithmique & Programmation Orientée Objet
Semestre 2 ST
La récursivité
Cours TD TP

  Problématique Définition  
Comment bien faire? Exemples

Version PDF

Clavier.class - Ecran.class - Documentation

Problématique

  • Dans certains cas, présentation des problèmes à résoudre sous forme récurrente
    • Formulation utilisée car c'est la plus naturelle ou tout simplement la seule existante
  • Forme récurrente : Situation connue à l'étape initiale, calcul de l'état à l'étape i à partir de l'état à l'étape i-1
  • Formalisation au moyen de deux ou trois items
    • Les conditions initiales (i.e. l'état du problème à étape 0)
    • Le processus permettant de calculer l'état à l'étape i à partir de l'état à l'étape i-1
    • Eventuellement une condition définissant comment le processus récurrent doit se terminer
  • Exemple
    Les suites mathématiques : Définition d'une suite f par la donnée de f0, et par la formule de calcul de fi à partir de fi-1, suite infinie ou finie
  • Conditions initiales pas forcément définies par la seule donnée de l'étape 0
    • Etat initial plus n états suivants
    • Pour le calcul de l'état i, utilisation de l'état à l'étape i-1 mais aussi les n états qui l'ont précédé
  • Inconvénients d'une telle formulation pour une implantation informatique classique :
    • Nécessité d'une itération avec utilisation d'une boucle "pour" ou d'une boucle "tant que"
    • Nécessité d'une reformulation de la présentation récurrente
      • Risque que cette opération ne soit ni simple ni même possible
      • Risque de commettre une erreur au cours de cette reformulation
  • Exemple : La suite de Fibonacci Fib0 = 0, Fib1 = 1, Fibi = Fibi-1 + Fibi-2, suite infinie
    • Valeurs :
      • F0 = 0
      • F1 = 1
      • F2 = 1
      • F3 = 2
      • F4 = 3
      • F5 = 5
      • F6 = 8
      • F7 = 13
      • F8 = 21
      • F9 = 34
      • F10 = 55
      • ...
  • Implantation séquentielle classique du calcul de la valeur valeur de la suite de Fibonacci pour une valeur entière n donnée :
    • Une boucle "pour"
    • Deux variables auxiliaires pour stocker les deux dernières valeurs Fibi-1 et Fibi-2 calculées nécessaires au calcul de Fibi
    • Une fois Fibi connu, préparation des valeurs utilisées à l'itération suivante :
      • Variable Fibi-2 réaffectée avec Fibi-1
      • Variable Fibi-1 réaffectée avec Fibi

{ Fonction de calcul et retour                 }
{ de Fib(n) par methode sequentielle           }
{ Définition:                                  }
{  - Fib(0) = 0                                }
{  - Fib(1) = 1                                }
{  - Fib(n) = Fib(n-1)+Fib(n-2)                }
{ n : valeur pour laquelle Fib(n) est calculé  }

entier fonction fib(-> entier n)
  entier res
  entier a
  entier b
  entier i
  dans le cas de n
    0 :
    1 :
      res <- n
    autres cas :
      res <- 0
      a <- 0
      b <- 1
      pour i de 2 à n faire
        res <- a+b
        a <- b
        b <- res
      fait
  fcas
  retourner res
fin fonction

/* Fonction de calcul et retour                */
/* de Fib(n) par methode sequentielle          */
/* Définition:                                 */
/*  - Fib(0) = 0                               */
/*  - Fib(1) = 1                               */
/*  - Fib(n) = Fib(n-1)+Fib(n-2)               */
/* n : valeur pour laquelle Fib(n) est calculé */

static long fib(int n) {
  long res;
  long a;
  long b;
  switch (n) {
    case 0 :
    case 1 : {
      res = n; }
      break;
    default : {
      res = 0;
      a = 0;
      b = 1;
      for ( int i = 2 ; i <= n ; i++ ) {
        res = a+b;
        a = b;
        b = res; } }
      break; }
  return res;
}
FibonacciSequentiel.lda
FibonacciSequentiel.java
Exemple d'exécution
  • Solution plus directe : Utiliser la récursivité

La récursivité : Définition

  • Outil de développement proposé par la grande majorité des langages informatiques (Java, C, C++, ADA, Basic, Pascal, Lisp, ...)
  • Ecriture d'un sous-algorithme dont le corps contient un(plusieurs) appel(s) au sous-algorithme lui-même
  • Développement d'un sous-algorithme qui s'"utilise" lui-même de la même manière qu'une définition récurrente "s'utilise" elle-même dans la mesure où son terme récurrent définit l'état à étape i par référence à un(des) état(s) précédent(s)
  • Pas de syntaxe particulière pour indiquer l'utilisation de la récursivité en langage algorithmique ou en langage Java
  • Appel récursif en utilisant le nom de fonction et en passant en entête les paramètres effectifs nécessaires
  • Exemple : La suite de Fibonacci

{ Fonction de calcul et retour                 }
{ de Fib(n) par methode recursive              }
{ Définition:                                  }
{  - Fib(0) = 0                                }
{  - Fib(1) = 1                                }
{  - Fib(n) = Fib(n-1)+Fib(n-2)                }
{ n : valeur pour laquelle Fib(n) est calculé  }

entier fonction fib(-> entier n)
  entier res
  dans le cas de n
    0 :
    1 :
      res <- n
    autres cas :
      res <- fib(n-1)+fib(n-2)
  fcas
  retourner res
fin fonction

/* Fonction de calcul et retour                */
/* de Fib(n) par methode recursive             */
/* Définition:                                 */
/*  - Fib(0) = 0                               */
/*  - Fib(1) = 1                               */
/*  - Fib(n) = Fib(n-1)+Fib(n-2)               */
/* n : valeur pour laquelle Fib(n) est calculé */

static long fib(int n) {
  long res;
  switch (n) {
    case 0 :
    case 1 : {
      res = n; }
      break;
    default : {
      res = fib(n-1)+fib(n-2); }
      break; }
  return res;
}
FibonacciRecursif.lda
FibonacciRecursif.java
Exemple d'exécution
  • Comparaison entre les versions séquentielle et récursive :
    • Disparition de la boucle "pour" et simplification apparente de l'écriture qui matche parfaitement à la définition récurrente
    • Boucle "pour" implicitement remplacée par une itération réalisée par la récursivité
      • Appel à Fib(n) -> appel à Fib(n-1) -> appel à Fib(n-2) et ainsi de suite jusqu'à Fib(1)
        -> Recréation implicite mais effectif du processus itératif conséquence de la boucle "pour"

Comment programmer la récursivité?

  • Programmation d'une fonction récursive -> Résolution de 2 problèmes :
    • Définition du terme récurrent (i.e. où et sous quelle forme l'appel (ou les appels) récursif est réalisé dans le corps de la fonction) et éventuellement de son initialisation
    • Définition de la condition sous laquelle l'appel (ou les appels) récursif n'est pas réalisé de façon que la récursivité soit interrompue
      • Assurance qu'il y aura bien systématiquement fin des appels récursifs successifs (implantation des conditions initiales ou d'une condition de terminaison)
  • Si non interruption de la récursivité :
    • Plantage avec une erreur de type "Stack overflow" (dépassement de capacité de la pile)
    • Erreur liée au fait que tout appel de fonction (récursif ou non) consomme une certaine quantité de mémoire pendant l'exécution de la fonction (en particulier mémoire nécessaire aux paramètres d'entête et aux variables locales de la fonction)
    • Mémoire allouée au sein d'une zone mémoire spécifique de taille limitée : la "pile"
    • Consommation d'un peu plus de mémoire à chaque appel récursif successif en profondeur jusqu'à atteindre la taille maximale
      -> Génération d'un "plantage" si la récursivité n'est pas stoppée
  • Remarque : Même dans le cas d'un fonctionnement normal, la taille finie de la pile limite la profondeur récursive maximale.
    -> Existence d'une limite inhérente à cet outil de programmation.
  • Exemple : La suite de Fibonacci
    • Terme récurrent : Fibn = Fibn-1 + Fibn-2
    • Conditions d'arrêt : Fib0 = 0, Fib1 = 1
    • n = 1 ou n = 0
      -> Condition d'arrêt vérifiée
      -> Pas d'amorçage de la récursivité
    • n plus grand que ou égal à 2
      -> Condition d'arrêt non vérifiée
      -> Amorçage de la récursivité
      -> Décréments de 1 lors du premier appel puis de 2 lors du second

Cas typiques d'utilisation de la récursivité

Utilisation fréquente de la récursivité dans les cas suivants :

  • Algorithmes implantant une méthode dichotomique
    • Recherches dichotomiques
    • Tris dichotomiques
    • ...
  • Algorithmes d'exploration
    • Parcours
    • Coloriage
    • ...

Exemples d'utilisation de la récursivité

  • Multiplier deux nombres entiers strictement positifs sans utiliser l'opérateur multiplication (difficulté faible)
  • a*b = b si a = 1
  • a*b = b+(a-1)*b si a <> 1
  • Inverser une chaîne de caractères (difficulté faible)
  • Inversion d'une chaîne de caractères st composée de plus de 1 caractère :
    • Extraction de la chaîne s formée du premier caractère de st
    • Concaténation de s à la fin de la chaîne de caractères obtenue par inversion de st moins son premier caractère
      inverse("abc") = inverse("bc")+"a"
  • Inversion d'une chaîne de caractères st composée de 0 ou 1 caractère :
    • Déjà inversée

{ Inversion d'une chaine de caracteres        }
{ st : la chaine de carateres à inverser      }

chaine fonction inversionChaine(-> chaine st)
  chaine s
  chaine s1
  chaine s2
  entier lst <- longueur(st)
  si ( lst == 0 ) ou ( lst == 1 ) alors
    s <- st
    sinon
    s1 <- substring(st,0,1) 
    s2 <- inversionChaine(substring(st,1,lst)) 
    s <- concatener(s2,s1)
  fsi
  retourner s
fin fonction

/* Inversion d'une chaine de caracteres        */
/* st : la chaine de carateres à inverser      */

static String inversionChaine(String st) {
  String s;
  String s1;
  String s2;
  int lst = st.length();
  if ( ( lst == 0 ) || ( lst == 1 ) ) {
    s = st; }
    else {
    s1 = st.substring(0,1); 
    s2 = inversionChaine(st.substring(1,lst)); 
    s = s2+s1; }
  return s;
}
InversionChaineCaracteres.lda
InversionChaineCaracteres.java
Exemple d'exécution
  • Trouver, sans utiliser sqrt, la racine carrée positive d'un nombre réel compris dans l'intervalle [0.0,1.0] (difficulté moyenne)
  • Détermination de la valeur y positive telle que y = f(x)
    où f est la fonction racine carrée et x est une valeur réelle positive contenue dans l'intervalle [0.0,1.0]
  • Valeur recherchée comprise dans l'intervalle [0.0,1.0]


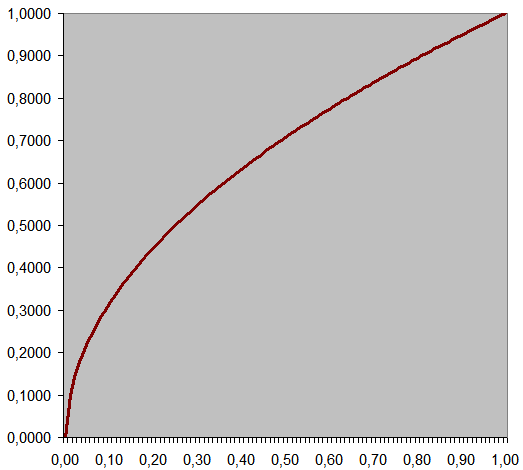
Fonction "Racine carrée" sur l'intervalle [0.0,1.0]

  • Reformulation du problème en y' = f-1(x')
    où y' = x, x' = y et f-1 est la fonction "carré" (inverse de racine carrée) que l'on peut implanter en multipliant une valeur par elle-même
  • Fonction f-1 continue et croissante sur l'intervalle [0.0,1.0]


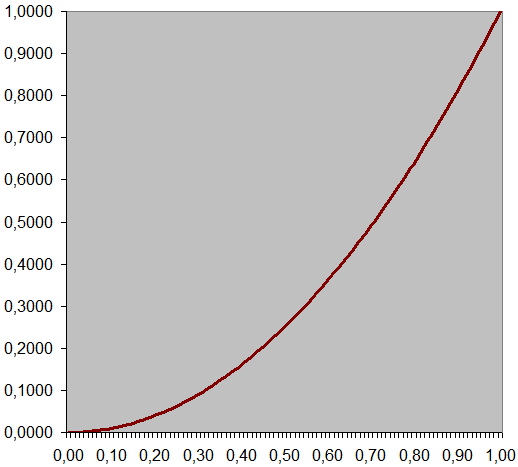
Fonction "Carré" sur l'intervalle [0.0,1.0]

  • Recherche de la valeur x' telle que x'*x'=y' (équivalent à y*y = x et donc y = racineCarree(x))
  • Technique dichotomique
  • Intervalle de recherche d'ouverture réduite d'un facteur 2.0 à chaque étape de recherche à partir de l'intervalle initial [0.0,1.0]
  • A chaque étape, déplacement de l'une des deux bornes pour adopter leur valeur moyenne m
  • Choix de la borne déplacée réalisé en comparant la valeur y' au carré de m (m*m)
    • Si m*m plus grand que y', report de la borne supérieure sur m
    • Si m*m plus petit que y', report de la borne inférieure sur m
  • "Relance" récursive sur le nouvel intervalle ainsi calculé
  • Implantation récursive
    -> Problème de l'arrêt de la récursivité
    • Implantation d'un test sur l'ouverture de l'intervalle
    • Arrêt quand ouverture inférieure à une valeur limite e
      -> Résultat : La valeur moyenne m
      -> Erreur commise inférieure à e

{ Constante de definition de la precision     }
{ de calcul                                   }

constante EPSILON reel <- 0.00000000001
  
{ Fonction recursive de calcul et retour      }
{ de la racine carree d'un nombre reel        }
{ x : le nombre dont la racine carrée         }
{     est calculée                            }
{ a : la borne minimale de l'intervalle       }
{     de recherche                            }
{ b : la borne minimale de l'intervalle       }
{     de recherche                            }

reel fonction racine(-> reel x,-> reel a,-> reel b)
  reel res
  reel m <- (b+a)/2.0
  si b-a > EPSILON alors
    si m*m > x alors
      res <- racine(x,a,m)
      sinon
      res <- racine(x,m,b)
    fsi
    sinon
    res <- m
  fsi
  retourner res
fin fonction
    
{ Fonction de calcul et retour                }
{ de la racine carree d'un nombre compris     }
{ dans l'intervalle [0.0,1.0]                 }
{ x : le nombre dont la racine carrée         }
{     est calculée                            }

reel fonction racineCarree(-> reel x)
  réel v <- racine(x,0.0,1.0)
  retourner v
fin fonction

/* Constante de definition de la precision     */
/* de calcul                                   */

static final double EPSILON = 0.00000000000001;

/* Fonction recursive de calcul et retour      */
/* de la racine carree d'un nombre reel        */
/* que l'on sait être comprise                 */
/* dans l'intervalle [a,b]                     */
/* x : le nombre dont on souhaite calculer     */
/*     la racine carree                        */
/* a : la borne minimale de l'intervalle       */
/*     de recherche                            */
/* b : la borne maximale de l'intervalle       */
/*     de recherche                            */

static double racine(double x,double a,double b) {
  double res;
  double m = (b+a)/2.0;
  if ( b-a > EPSILON ) {
    if ( m*m > x ) {
      res = racine(x,a,m); }
      else {
      res = racine(x,m,b); } }
    else {
    res = m; }
  return res;
}
  
/* Fonction de calcul et retour                */
/* de la racine carree d'un nombre reel        */
/* compris dans l'intervalle [0.0,1.0]         */
/* x : le nombre dont on souhaite calculer     */
/*     la racine carree                        */

static double racineCarree(double x) {
  double v = racine(x,0.0,1.0);
  return v;
}
RacineCarree.lda
RacineCarree.java
Exemple d'exécution
  • Parcourir un labyrinthe sans cycle (difficulté moyenne)
  • Labyrinthe :
    Matrice de booléens où les vrais codent pour les couloirs
    Couloirs "épais" de 1 booléen
    Déplacements autorisés à "droite", à "gauche", en "haut" et en "bas" si booléen à vrai dans cette direction
    Entrée par une cellule à vrai située sur le bord
    Sortie par une autre cellule, s'il en existe une, située sur le bord
  • Parcours :
    Parcours possible d'une cellule si elle est à vrai
    Continuation du parcours à partir d'une cellule en lançant récursivement l'algorithme de parcours sur les 0, 1 ou 2 cellules voisines qui sont accessibles et qui ne sont pas la cellule par où on est arrivé

FFFFFFFFFFFFFFFFFFFF
FVVVVVVVVVVVVVVVVFFF
FVFFVFFFFFFFFFVFFFFF
VVFFVFFFVVVVVFVFFFFF
FFFFVFFFVFFFFFVFFFFF
FFFFVFFVVVVFVVVVVVFF
FFVVVFFFFFVFVFFFFVFF
FFVFFFFFFFVFVFFFFVFF
FFVFFVFFFFVFFFVFFVFF
FFVFFVVVVVVFFFVFFVFF
FFVFFFFVFFFFFFVVVVVF
FFVVVVVVVVVVVFFVFFFF
FFFFVFFVFFFFVFFVVVFF
FVFFVFFFFFFFVFFFFVFF
FVFFFFVVVVVVVFFFFFFF
FVVFFFVFFFFFFFFFVVVV
FFVFFFVFVVVVVFFFVFFF
FFVFFFVFVFFFFFFFVFFF
FFVVVVVVVVVVVVVVVFFF
FFFFFFFFFFFFFFFFFFFF

/* Type structure de definition d'une position    */
/* par un numero de ligne et un numero de colonne */

static class Position {
  int l = -1;
  int c = -1; };

/* Test d'egalite de deux position                */

static boolean egal(Position p1,Position p2) {
  boolean res;
  if ( ( p1.c != p2.c ) || ( p1.l != p2.l ) ) {
    res = false; }
    else {
    res = true; }
  return res;
}    

/* Fonction de test de l'existence d'une sortie   */
/* a un labyrinthe represente par un tableau      */
/* de booleen                                     */
/* La matrice lb code le labyrinthe               */
/* Le parametre p est la position a partir        */
/* de laquelle rechercher                         */
/* Le parametre origine est la position qui vient */
/* d'etre quittee pour atteindre la position p et */
/* vers laquelle il est interdit de retourner     */
/* Le parametre sortie est destine a recueillir   */
/* la position de la sortie si celle-ci existe    */
/* Le booleen retourne indique si une sortie      */
/* a ete trouvee                                  */

static boolean trouveSortie(boolean [][] lb,
                            Position p,
                            Position origine,
                            Position sortie) {
  boolean res = false;
  Position np = new Position();
  if ( ( p.l == -1 ) || ( p.l == lb.length ) ||
       ( p.c == -1 ) || ( p.c == lb[0].length ) ) {
    sortie.l = origine.l;
    sortie.c = origine.c;
    res = true; }
    else {
    if ( lb[p.l][p.c] == true ) {
      np.c = p.c+1;
      np.l = p.l;
      if ( egal(np,origine) == false ) {
        res = trouveSortie(lb,np,p,sortie); }
      if ( res == false ) {
        np.c = p.c-1;
        np.l = p.l;
        if ( egal(np,origine) == false ) {
          res = trouveSortie(lb,np,p,sortie); }
        if ( res == false ) {
          np.c = p.c;
          np.l = p.l+1;
          if ( egal(np,origine) == false ) {
            res = trouveSortie(lb,np,p,sortie); }
          if ( res == false ) {
            np.c = p.c;
            np.l = p.l-1;
            if ( egal(np,origine) == false ) {
              res = trouveSortie(lb,np,p,sortie); } } } } } }
  return(res);
}
Labyrinthe.java
Exemple d'exécution
  • Parcourir des arborescences (difficulté importante)
  • Arborescence : Structure informatique mimant un arbre
    • Composée de noeuds et d'arêtes reliant ces noeuds
    • Un et un seul chemin entre tout couple de noeuds
  • Désignation usuelle d'un noeud comme étant la "racine" de l'arborescence
    • Généralement utilisée pour la repérer car accès possible à tous les autres noeuds en "descendant" (ou "montant" suivant le vocabulaire employé) dans l'arborescence à partir de la racine
  • Pour un noeud n :
    • Noeud "père" : Premier noeud sur le chemin partant de n en direction de la racine
    • Noeuds "fils" : Autres noeuds que le noeud père connectés à n
  • "Feuille" (noeud terminal) : Noeud sans fils
  • Seul noeud sans père : Le noeud racine
  • Arborescence binaire : Arborescence pour laquelle aucun noeud n'a plus de 2 fils
  • Arborescence binaire stricte : Arborescence où chaque noeud possède soit 2, soit 0 fils
    • Parcours une arborescence
  • Utilisation naturelle de la récursivité pour manipuler les arborescences (binaires ou non) dont on ne connaît généralement que la racine
  • Réalisation de toutes les opérations nécessitant un parcours complet en lançant la fonction récursive de traitement sur la racine
  • Programmation du corps de la fonction pour lancer successivement une exécution récursive sur tous les sous-arbres (sous-arbre "droit" puis sous-arbre "gauche" (ou l'inverse) pour les arbres binaires strictes) du noeud passé en paramètre
    • Modélisation d'une arborescence en langage Java
      • Méthode 1 : Un tableau de noeuds
  • Arborescence codée dans un tableau de Noeud
    Pour chaque noeud :
      - Champ pere : indice du noeud père dans le tableau de noeuds de l'arborescence
      - Champs fils : indices des fils dans le tableau de noeuds de l'arborescence
    Valeur d'indice égale à -1 -> Pas de père ou pas de fils
    Noeud racine placé à l'indice 0 du tableau et seul noeud dont l'indice du père est égal à -1
    Noeuds internes caractérisés par le fait que l'indice d'au moins un de leurs fils est différent de -1
    Noeuds terminaux caractérisés par le fait que l'indice de tous leurs fils est égal à -1
  • Type agrégé java pour représenter un noeud d'une arborescence binaire (0, 1 ou 2 fils) :
    static class Noeud {
      int pere = -1;             // Indice du noeud pere
      int filsDroit = -1;        // Indice du noeud fils droit
      int filsGauche = -1; };    // Indice du noeud fils gauche
  • Type agrégé java pour représenter un noeud d'une arborescence où chaque noeud peut avoir un nombre arbitraire de fils :
    static class Noeud {
      int pere = -1;             // Indice du noeud pere
      int [] fils;               // Indices des noeuds fils
  • Exemple d'arborescence binaire
Indice Père FilsDroit FilsGauche
0 -1 1 3
1 0 2 -1
2 1 -1 -1
3 0 4 5
4 3 6 7
5 3 8 9
6 4 -1 -1
7 4 -1 -1
8 5 -1 10
9 5 11 12
10 8 -1 -1
11 9 13 14
12 9 15 16
13 11 -1 -1
14 11 -1 -1
15 12 -1 -1
16 12 17 18
17 16 -1 -1
18 16 -1 -1

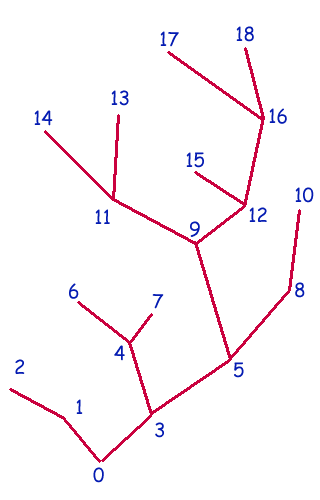Arborescence binaire modélisée
par le tableau de noeuds ci-contre
  • Exemples :
    • Recherche du nombre de noeuds d'une arborescence
    • Recherche de la distance maximale existant entre la racine et l'ensemble des feuilles d'une arborescence : la profondeur d'une arborescence

/* Structure de stockage d'un noeud            */
/* d'arborescence                              */

static class Noeud {
  int pere = -1;
  int filsDroit = -1;
  int filsGauche = -1; };

/* Calcul du nombre de noeuds                  */
/* d'une arborescence                          */

static int taille(Noeud [] tn,int n) {
  int nb;
  if ( n == -1 ) {
    nb = 0; }
    else {
    nb = 1 + taille(tn,tn[n].filsDroit)
           + taille(tn,tn[n].filsGauche); }
  return nb;
}

/* Calcul de la profondeur d'une arborescence  */

static int profondeur(Noeud [] tn,int n) {
  int prf;
  int prfd;
  int prfg;
  if ( n == -1 ) {
    prf = 0; }
    else {
    prfd = profondeur(tn,tn[n].filsDroit);
    prfg = profondeur(tn,tn[n].filsGauche);
    if ( prfd > prfg ) {
      prf = 1 + prfd; }
      else {
      prf = 1 + prfg; } }
  return prf;
}
Arborescence.java
Exemple d'exécution
      • Méthode 2 (java niveau "expert")
  • Arborescence codée dans des variables Noeud individuelles (pas dans un tableau) et représentées par leurs adresses mémoire
    Pour chaque noeud :
      - Champ pere : Noeud père
      - Champs fils : Noeuds fils
    Valeur de père ou fils égale à null (constante java équivalente à l'adresse 0x00000000) -> Pas de père ou pas de fils
    Noeud racine : seul noeud dont le champ père est égal à null
    Noeuds internes caractérisés par le fait qu'au moins un de leurs fils est différent de null
    Noeuds terminaux caractérisés par le fait tous leurs fils sont égaux à null
  • Type agrégé java pour une arborescence quelconque :
    static class Noeud {
      Noeud pere = null;              // Noeud pere
      Noeud [] fils; };               // Tableau des noeuds fils
  • Type agrégé java pour une arborescence binaire :
    static class Noeud {
      Noeud pere = null;              // Noeud pere
      Noeud [] fils; };               // Tableau des noeuds fils
  • Type agrégé java pour une arborescence binaire stricte :
    static class Noeud {
      Noeud pere = null;              // Noeud pere
      Noeud filsDroit = null;         // Noeud fils droit
      Noeud filsGauche = null; };     // Noeud fils gauche
  • Exemples :
    • Recherche du nombre de noeuds d'une arborescence
    • Recherche de la distance maximale existant entre la racine et l'ensemble des feuilles d'une arborescence

/* Structure de stockage d'un noeud            */
/* d'arborescence                              */

static class Noeud {
  Noeud pere = null;
  Noeud filsDroit = null;
  Noeud filsGauche = null; };

/* Calcul du nombre de noeuds                  */
/* d'une arborescence                          */

static int taille(Noeud n) {
  int nb;
  if ( n == null ) {
    nb = 0; }
    else {
    nb = 1 + taille(n.filsDroit)
           + taille(n.filsGauche); }
  return nb;
}

/* Calcul de la profondeur d'une arborescence  */

static int profondeur(Noeud n) {
  int prf;
  int prfd;
  int prfg;
  if ( n == null ) {
    prf = 0; }
    else {
    prfd = profondeur(n.filsDroit);
    prfg = profondeur(n.filsGauche);
    if ( prfd > prfg ) {
      prf = 1 + prfd; }
      else {
      prf = 1 + prfg; } }
  return prf;
}
ArborescenceBinaire.java
Exemple d'exécution