Première partie

Implantation en langage Java et validation des exercices de TD

Seconde partie: Exercices supplémentaires

Exercice n°1

Le PGCD (Plus Grand Commun Diviseur) de 2 nombres entiers positifs a et b est, comme son nom l'indique, le nombre entier positif n de valeur maximale tel que a est divisible par n et b est divisible par n.
Le calcul "classique" du PGCD de 2 nombres entiers fait appel à la décomposition en facteurs premiers de chacun des 2 nombres. Ce n'est pas cette méthode qui est le sujet de cet exercice.
Une autre méthode de calcul existe, basée sur la définition suivante:
  - Si a < b, PGCD(a,b) = PGCD(b,a)
  - Si a >= b et si b = 0, PGCD(a,b) = a
  - Si a >= b et si b != 0, PGCD(a,b) = PGCD(b,a modulo b)
Implanter un sous-algorithme de calcul du PGCD de deux nombres entiers positifs.

Exercice n°2

Un tableau de booléens est utilisé pour stocker une structure formée de cellules carrées selon les modalités suivantes:
  - Chaque cellule peut être connectée à 4 autres cellules: celles situées immédiatement à droite, à gauche, en haut et en bas.
  - Une cellule de la structure est repérée dans le tableau par la valeur vrai. Les faux indiquent donc les cellules qui ne font pas partie de la structure.
  - Aucune cellule de la première ligne, de la dernière ligne, de la première colonne et de la dernière colonne n'est configurée à vrai.
  - Aucun cycle n'existe permettant de revenir à une cellule par un autre chemin que celui employé pour s'en éloigner.
Une telle structure est obligatoirement arborescente et présente des branches épaisses d'une cellule. Elle pourra par exemple être utilisée pour représenter un labyrinthe formé de couloirs et d'embranchements.

a) On connait les coordonnées d'une cellule dont le contenu est le booléen vrai. Développer un sous-algorithme permettant d'afficher à l'écran les coordonnées de l'ensemble des cellules faisant partie de la structure.

b) On connait les coordonnées d'une cellule dont le contenu est le booléen vrai. Développer un sous-algorithme permettant de calculer le nombre de cellules faisant partie de la structure.

c) On connait les coordonnées d'une cellule c dont le contenu est le booléen vrai. Développer un sous-algorithme permettant de calculer la distance la plus longue (comptée en nombre de cellules) existant entre la cellule c et l'ensemble des cellules terminales de la structure. Une cellule terminale est une cellule connectée à une et une seule cellule.

d) On connait les coordonnées d'une cellule dont le contenu est le booléen vrai. Développer un sous-algorithme permettant de calculer l'élongation de la structure. On appelle élongation la distance maximale entre deux cellules terminales.

e) Développer un sous-algorithme permettant de générer une structure au hasard dans une matrice de nxm booléens.

Exercice n°3

On souhaite implanter une fonction permettant de calculer la chaine de caractères expansée sur n niveaux d'un caractère selon les règles suivantes:
  - La chaine initiale est composée d'un seul caractère qui ne peut être que 'a', 'b' ou 'c'.
  - A chaque niveau, chaque 'a' évolue en "bc".
  - A chaque niveau, chaque 'b' évolue en "ca".
  - A chaque niveau, chaque 'c' évolue en "a".

Exemple: L'expansion de la chaine "a" donne "a", "bc", "caa", "abcbc","bccaacaa", "caaabcbcabcbc" aux étapes 0, 1, 2, 3, 4 et 5.

Exercice n°4

On souhaite implanter une fonction d'affichage du flocon de Koch au niveau n. Le flocon de Koch est une courbe fractale obtenue par transformation récursive d'un segment de droite en 4 segments de droite selon le schéma ci-dessous.

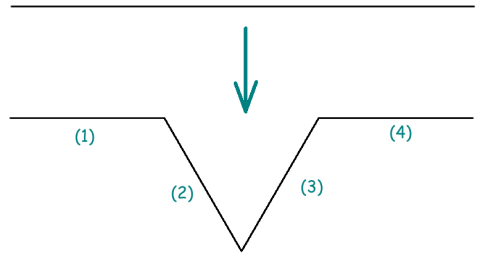
Le sous-segment (1) correspond au premier tier du segment initial. Le sous-segment (4) correspond au troisième tier du segment initial. Les sous-segments (2) et (3) remplacent le tier central tc du segment initial. Ils correspondent aux 2 autres cotés du triangle équilatéral dont tc est un des cotés. Ainsi du niveau 0 au niveau 4, les images suivantes sont obtenues.

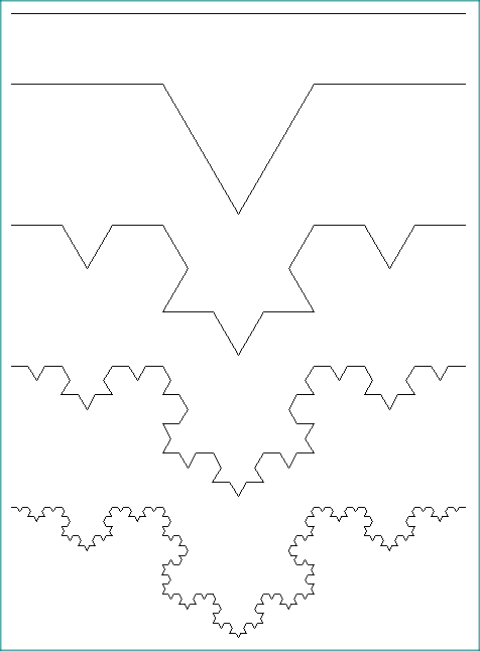
Mode graphique

La création d'affichages graphiques est à réaliser au moyen de l'API EcranGraphique développée à cette fin. Celle-ci peut être téléchargée en cliquant sur le lien suivant: EcranGraphique.zip. Le fichier zip obtenu contient 4 fichiers .class qu'il convient d'extraire dans le répertoire où sera placé le fichier .java développé pour le projet. La documentation javadoc de référence de cette API est disponible via le lien suivant: Documentation javadoc EcranGraphique. Un exemple d'utilisation est proposé au lien suivant: TestEcranGraphique.java (exécution).

Les fonctionnalités principales de cette API sont:

• Paramétrage et ouverture d'une fenêtre de dessin
• Choix de la couleur de tracé
• Tracé d'un pixel selon la couleur de tracé
• Tracé d'un segment de droite selon la couleur de tracé
• Tracé d'une chaîne de caractères selon la couleur de tracé
• Activation/désactivation du mode de tracé "ou exclusif"
• Choix de la couleur d'effacement de la zone de tracé
• Effacement de la zone de tracé avec la couleur d'effacement
• Récupération des touches de clavier frappées
• Récupération des boutons de souris utilisés
• Récupération des positions en x et en y de la souris

Apres ouverture de la fenêtre de dessin, la création d'une image suit le schéma suivant:

• Effacement de l'image par EcranGraphique.clear()
• Exécution de tous les appels de fonction correspondant au éléments graphiques à tracer par EcranGraphique.draw*()
• Appel à la fonction EcranGraphique.flush() pour afficher l'image obtenue

Les coordonnées utilisées sont comptées en pixels. Le repère d'affichage est orienté avec l'axe des x en direction de la droite et l'axe des y en direction du bas de la fenêtre d'affichage. L'origine (coordonnées (0,0)) est située en haut à gauche de la fenêtre.

Exercice n°5

La variable matrice d'entier lb ci-dessous décrit un labyrinthe:
int [][] lb = { { 0,0,0,0,0,0,0,0,0,0,0,0 },
                { 0,1,0,1,1,1,0,1,1,1,1,0 },
                { 0,1,0,1,0,0,0,1,0,1,0,0 },
                { 0,1,1,1,1,1,0,1,0,1,1,0 },
                { 0,1,0,0,0,1,0,0,0,1,0,0 },
                { 0,1,0,1,1,1,1,1,1,1,1,0 },
                { 0,1,0,0,0,1,0,0,1,0,0,0 },
                { 0,1,1,0,0,1,0,1,1,1,1,0 },
                { 0,0,0,0,0,1,0,9,0,0,1,0 },
                { 0,0,0,0,0,0,0,0,0,0,0,0 } };

Les cellules 1 sont les cellules accessibles. Les cellules 0 sont les "murs". L'entrée est la cellule de coordonnées (1,1). La sortie, si elle existe, est la cellule numérotée 9.

a) Développer une fonction récursive permettant d'explorer le labyrinthe pour déterminer s'il y a une sortie ou non.

b) Développer une fonction récursive permettant d'explorer le labyrinthe à la recherche des coordonnées de la cellule de sortie pour les afficher à l'écran.

c) Développer une fonction récursive permettant d'explorer le labyrinthe à la recherche des coordonnées de la cellule de sortie pour les retourner comme résultat de fonction.

d) Il peut exister plusieurs sorties. Développer une fonction récursive permettant d'explorer le labyrinthe à la recherche des coordonnées de la cellule de sortie la plus proche de l'entrée pour les retourner comme résultat de fonction.