Algorithmique-Programmation Orientée Objet Semestre 2 ST - Récursivité

Algorithmique & Programmation Orientée Objet
Semestre 2 ST
La récursivité

Cours

TP - Corrections

Clavier.class - Ecran.class - Chaine.class - Documentation

Exercice n°1: Calcul de factoriel

La définition récurrente du calcul de n! est:
- 0! = 1
- n! = n * (n-1)!

Implanter un sous-algorithme de calcul de n! en utilisant la récursivité.

/* Fonction de calcul et retour                 */
/* de n! par methode récursive                  */
/* Définition:                                  */
/*  - 0! = 1                                    */
/*  - n! = (n-1)!*n                             */
/* n : valeur pour laquelle n! est calculé      */

static long factoriel(int n) {
  long res;
  if ( n == 0 ) {
    res = 1; }
    else {
    res = factoriel(n-1)*n; }
  return res;
}

Clavier.class - Ecran.class - Exemple d'exécution

Exercice n°2: Inversion d'une chaîne de caractères par décomposition dichotomique

Utiliser la technique de décomposition dichotomique pour implanter un sous-algorithme récursif d'inversion d'une chaîne de caractères:
- Une chaîne de 0 ou 1 caractère est déjà inversée.
- Une chaîne s de n caractères où n est supérieur à 1 peut être inversée en concaténant s2 et s1 où s1 est la chaîne obtenue par inversion de la 1/2 sous-chaîne comportant les n/2 premiers caractères de s et s2 est la chaîne obtenue par inversion de la 1/2 sous-chaîne comportant les n-n/2 derniers caractères de s.

On pourra utiliser la fonction suivante pour extraire une sous-chaîne de caractères d'une chaîne de caractères:
chaîne fonction sousChaine(-> chaine s,-> entier indi,-> entier indf)
où s est la chaîne où l'extraction est réalisée, indi est l'indice du caractère de s à partir duquel l'extraction est réalisée et indf est l'indice du caractère qui suit immédiatement le dernier caractère extrait de s (i.e. le nombre de caractères extraits est égal à indf-indi).

InversionChaineMethodeDichotomique.java

/* Fonction de calcul et retour de l'inverse   */
/* d'une chaine de caracteres                  */
/* st : la chaine de carateres à inverser      */

static String inversionChaine(String st) {
  String s;
  String s1;
  String s2;
  int l1;
  int lst = st.length();
  if ( ( lst == 0 ) || ( lst == 1 ) ) {
    s = st; }
    else {
    l1 = lst/2;
    s1 = inversionChaine(st.substring(0,l1));
    s2 = inversionChaine(st.substring(l1,lst));
    s = s2+s1; }
  return s;
}

Clavier.class - Ecran.class - Chaine.class - Exemple d'exécution

Exercice n°3: "Coloration" dans un tableau d'entiers

On considère un tableau d'entiers de taille NxM. Ce tableau code une image où chacun des entiers code la couleur d'un pixel.
On souhaite colorier des zones de pixels.

a) Développer un sous-algorithme de coloriage, au moyen d'une couleur, de la zone de pixels définie par les règles suivantes:
(1) Un premier pixel de coordonnées (x,y) est colorié s'il a une couleur différente de la couleur de tracé. Si ce n'est pas le cas le coloriage s'arrête.
(2) Un pixel de couleur identique à la couleur du premier pixel colorié et non encore colorié touche (par la gauche, par la droite, par le haut ou par le bas) un pixel qui a été colorié.
(3) Tant qu'il existe des pixels vérifiant la règle (2), on les colorie avec la couleur de tracé.
Ce sous-algorithme permet de "remplir" une tache de couleur uniforme uniformément avec une autre couleur.

Exemples
Appeler le sous-algorithme sur un pixel bleu aura pour conséquence
de remplir entièrement la tache bleue avec la couleur de tracé.
Appeler le sous-algorithme sur un pixel rose aura pour conséquence
de remplir entièrement la tache rose avec la couleur de tracé.
Appeler le sous-algorithme sur un pixel vert aura pour conséquence
de remplir entièrement la tache verte avec la couleur de tracé.
Appeler le sous-algorithme sur un pixel jaune aura pour conséquence
de remplir entièrement (jusqu'au bord) la tache jaune avec la couleur de tracé.
Appeler le sous-algorithme sur un pixel ayant la même couleur
que la couleur de tracé n'entrainera pas de remplissage.

b) Développer un sous-algorithme de coloriage, au moyen d'une couleur, de la zone de pixels définie par les règles suivantes:
(1) Un premier pixel de coordonnées (x,y) est colorié s'il a une couleur différente d'une couleur limite. Si ce n'est pas le cas le coloriage s'arrête.
(2) Un pixel de couleur différente de la couleur limite et non encore colorié touche (par la gauche, par la droite, par le haut ou par le bas) un pixel qui a été colorié.
(3) Tant qu'il existe des pixels vérifiant la règle (2), on les colorie avec la couleur de tracé.
Ce sous-algorithme permet de "remplir" uniformément avec une couleur une tache de couleur non-uniforme délimitée par une couleur uniforme.

Exemples
Appeler le sous-algorithme sur un pixel bleu, rose ou vert
avec comme couleur limite la couleur jaune aura pour conséquence
de remplir entièrement les taches bleue, rose et verte avec la couleur de tracé.
Si la couleur limite est le rose, désigner un pixel jaune, bleu ou vert
aura pour conséquence le remplissage des taches bleue et verte
ainsi que le remplissage de la tache jaune jusqu'au bord.
Désigner un pixel ayant la même couleur
que la couleur limite n'entrainera pas de remplissage.

ColoriageRecursif.java

/* Fonction recursive de coloriage d'une zone   */
/* de pixels de valeurs identiques              */
/* px : La position en x du pixel germe         */
/* py : la position en y du pixel germe         */
/* t  : la matrice des valeurs des pixels       */
/* c  : la couleur de remplissage               */
/* ct : la couleur de la tache à remplir        */

static void coloriageRecursif(int px,int py,int [][] t,
                              int c,int ct) {
  if ( ( px >= 0 ) && ( px < t[0].length ) &&
       ( py >= 0 ) && ( py < t.length ) ) {
    if ( ( t[py][px] != c ) && ( t[py][px] == ct ) ) {
      t[py][px] = c;
      coloriageRecursif(px+1,py,t,c,ct);
      coloriageRecursif(px-1,py,t,c,ct);
      coloriageRecursif(px,py+1,t,c,ct);
      coloriageRecursif(px,py-1,t,c,ct); } }
}

/* Fonction de coloriage d'une zone de pixels   */
/* de valeurs identiques                        */
/* px : La position en x du pixel germe         */
/* py : la position en y du pixel germe         */
/* t  : la matrice des valeurs des pixels       */
/* c  : la couleur de remplissage               */

static void coloriage(int px,int py,int [][] t,int c) {
  coloriageRecursif(px,py,t,c,t[py][px]);
}

/* Fonction recursive de remplissage d'une zone */
/* de pixels delimitee par une valeur           */
/* px : La position en x du pixel germe         */
/* py : la position en y du pixel germe         */
/* t  : la matrice des valeurs des pixels       */
/* c  : la couleur de remplissage               */
/* cl : la couleur de delimitation              */
/*      de la tache à remplir                   */

static void remplissageRecursif(int px,int py,int [][] t,
                                int c,int cl) {
  if ( ( px >= 0 ) && ( px < t[0].length ) &&
       ( py >= 0 ) && ( py < t.length ) ) {
    if ( ( t[py][px] != c ) && ( t[py][px] != cl ) ) {
      t[py][px] = c;
      remplissageRecursif(px+1,py,t,c,cl);
      remplissageRecursif(px-1,py,t,c,cl);
      remplissageRecursif(px,py+1,t,c,cl);
      remplissageRecursif(px,py-1,t,c,cl); } }
}

Clavier.class - Ecran.class - Exemple d'exécution

Exercice n°4: Calcul de combinaisons

On considère n caractères. Développer un sous-algorithme récursif d'affichage de toutes les combinaisons de ces n caractères.

AffichageCombinaisons.java

/* Affichage de toutes les combinaisons        */
/* de n valeurs existant un ensemble           */
/* de n valeurs                                */
/* Application a un tableau de caracteres      */

static void affichage(char [] e,char [] t,int nb) {
  char v;
  if ( nb == t.length ) {
    for ( int i = 0 ; i < nb ; i++ ) {
      Ecran.afficher(t[i]); }
    Ecran.afficherln(); }
    else {
    for ( int i = 0 ; i < e.length-nb ; i++ ) {
      t[nb] = e[i];
      v = e[i];
      e[i] = e[e.length-nb-1];
      affichage(e,t,nb+1);
      e[e.length-nb-1] = e[i];
      e[i] = v; } }
}

Clavier.class - Ecran.class - Exemple d'exécution

Exercice n°5: Affichages par récursivité

Précision: Pour les questions suivantes, on ne dispose ni du "pour" ni du "tant que".

a) On considère un nombre entier n positif ou nul. Développer un sous-algorithme permettant d'afficher en ordre décroissant la liste des nombres entiers compris dans l'intervalle [0,n].

b) On considère un nombre entier n positif ou nul. Développer un sous-algorithme permettant d'afficher en ordre croissant la liste des nombres entiers compris dans l'intervalle [0,n].

c) On considère un nombre entier n positif ou nul. Développer un sous-algorithme permettant d'afficher en ordre décroissant puis par ordre croissant la liste des nombres entiers compris dans l'intervalle [0,n].

d) On considère un nombre entier n positif ou nul. Développer un sous-algorithme permettant d'afficher en ordre croissant puis par ordre décroissant la liste des nombres entiers compris dans l'intervalle [0,n].

e) On considère un nombre entier n positif ou nul. Développer un sous-algorithme permettant d'afficher n par affichage individuel de ses chiffres.

AffichagesRecursifs.java

/* Fonction d'affichage par ordre decroissant  */
/* des nombres entiers compris entre 0 et n    */
/* n : valeur limite pour l'affichage          */

static void affichageDecroissant(int n) {
  Ecran.afficherln(n);
  if ( n > 0 )
    affichageDecroissant(n-1);
}

/* Fonction d'affichage par ordre croissant    */
/* des nombres entiers compris entre v et n    */
/* v : valeur minimale                         */
/* n : valeur limite pour l'affichage          */

static void affichageCroissant(int v,int n) {
  Ecran.afficherln(v);
  if ( v < n )
    affichageCroissant(v+1,n);
}

/* Fonction d'affichage par ordre croissant    */
/* des nombres entiers compris entre 0 et n    */
/* n : valeur limite pour l'affichage          */

static void affichageCroissant(int n) {
  affichageCroissant(0,n);
}

/* Affichage par ordre croissant               */
/* des nombres entiers compris entre 0 et n    */
/* Solution elegante                           */
/* n : valeur limite pour l'affichage          */

static void affichageCroissant2(int n) {
  if ( n > 0 )
    affichageCroissant2(n-1);
  Ecran.afficherln(n);
}

/* Affichage par ordre decroissant             */
/* puis par ordre croissant                    */
/* des nombres entiers compris entre 0 et n    */
/* n : valeur limite pour l'affichage          */

static void affichageDecroissantCroissant(int n) {
  Ecran.afficherln(n);
  if ( n > 0 )
    affichageDecroissantCroissant(n-1);
  Ecran.afficherln(n);
}

/* Affichage par ordre croissant               */
/* puis par ordre decroissant                  */
/* des nombres entiers compris entre v et n    */
/* v : valeur minimale                         */
/* n : valeur limite pour l'affichage          */

static void affichageCroissantDecroissant(int v,int n) {
  Ecran.afficherln(v);
  if ( v < n )
    affichageCroissantDecroissant(v+1,n);
  Ecran.afficherln(v);
}

/* Affichage par ordre croissant               */
/* puis par ordre decroissant                  */
/* des nombres entiers compris entre 0 et n    */
/* n : valeur limite pour l'affichage          */

static void affichageCroissantDecroissant(int n) {
  affichageCroissantDecroissant(0,n);
}

/* Fonction void d'ffichage des chiffres       */
/* d'un nombre entier                          */
/* n : nombre entier à afficher                */

static void affichage(int n) {
  if ( n >= 10 )
    affichage(n/10);
  Ecran.afficher(n%10);
}

Clavier.class - Ecran.class - Exemple d'exécution

Seconde partie: Exercices supplémentaires

Exercice n°1

Le PGCD (Plus Grand Commun Diviseur) de 2 nombres entiers positifs a et b est, comme son nom l'indique, le nombre entier positif n de valeur maximale tel que a est divisible par n et b est divisible par n.
Le calcul "classique" du PGCD de 2 nombres entiers fait appel à la décomposition en facteurs premiers de chacun des 2 nombres. Ce n'est pas cette méthode qui est le sujet de cet exercice.
Une autre méthode de calcul existe, basée sur la définition suivante:
- Si a < b, PGCD(a,b) = PGCD(b,a)
- Si a >= b et si b = 0, PGCD(a,b) = a
- Si a >= b et si b != 0, PGCD(a,b) = PGCD(b,a modulo b)
Implanter un sous-algorithme de calcul du PGCD de deux nombres entiers positifs.

PGCDRecursif.java

/* Fonction de calcul et retour du PGCD         */
/* de 2 nombres entiers positifs                */
/* par methode recursive                        */
/* a : Le premier nombre entier                 */
/* b : Le second nombre entier                  */

static int PGCD(int a,int b) {
  int res = 0;
  if ( a < b ) {
    res = PGCD(b,a); }
    else {
    if ( b == 0 ) {
      res = a; }
      else {
      res = PGCD(b,a % b); } }
  return res;
}

Clavier.class - Ecran.class - Exemple d'exécution

Exercice n°2

Un tableau de booléens est utilisé pour stocker une structure formée de cellules carrées selon les modalités suivantes:
- Chaque cellule peut être connectée à 4 autres cellules: celles situées immédiatement à droite, à gauche, en haut et en bas.
- Une cellule de la structure est repérée dans le tableau par la valeur vrai. Les faux indiquent donc les cellules qui ne font pas partie de la structure.
- Aucune cellule de la première ligne, de la dernière ligne, de la première colonne et de la dernière colonne n'est configurée à vrai.
- Aucun cycle n'existe permettant de revenir à une cellule par un autre chemin que celui employé pour s'en éloigner.
Une telle structure est obligatoirement arborescente et présente des branches épaisses d'une cellule. Elle pourra par exemple être utilisée pour représenter un labyrinthe formé de couloirs et d'embranchements.

a) On connait les coordonnées d'une cellule dont le contenu est le booléen vrai. Développer un sous-algorithme permettant d'afficher à l'écran les coordonnées de l'ensemble des cellules faisant partie de la structure.

b) On connait les coordonnées d'une cellule dont le contenu est le booléen vrai. Développer un sous-algorithme permettant de calculer le nombre de cellules faisant partie de la structure.

c) On connait les coordonnées d'une cellule c dont le contenu est le booléen vrai. Développer un sous-algorithme permettant de calculer la distance la plus longue (comptée en nombre de cellules) existant entre la cellule c et l'ensemble des cellules terminales de la structure. Une cellule terminale est une cellule connectée à une et une seule cellule.

d) On connait les coordonnées d'une cellule dont le contenu est le booléen vrai. Développer un sous-algorithme permettant de calculer l'élongation de la structure. On appelle élongation la distance maximale entre deux cellules terminales.

e) Développer un sous-algorithme permettant de générer une structure au hasard dans une matrice de nxm booléens.

ParcoursLabyrinthe.java

/* Fonction recursive de parcours              */
/* d'un labyrinthe avec affichage              */
/* des coordonnees des cellules                */

static void parcours(boolean [][] lb,int lo,int co,int l,int c) {
  if ( lb[l][c] ) {
    Ecran.afficherln(l," ",c);
    if ( ( l-1 != lo ) || ( c != co ) ) {
      parcours(lb,l,c,l-1,c); }
    if ( ( l+1 != lo ) || ( c != co ) ) {
      parcours(lb,l,c,l+1,c); }
    if ( ( l != lo ) || ( c-1 != co ) ) {
      parcours(lb,l,c,l,c-1); }
    if ( ( l != lo ) || ( c+1 != co ) ) {
      parcours(lb,l,c,l,c+1); } }
}

/* Fonction recursive de calcul de la longueur */
/* d'un labyrinthe                             */

static int longueur(boolean [][] lb,Position po,Position p) {
  int lng = 0;
  Position ps = new Position();
  if ( lb[p.l][p.c] ) {
    lng = 1;
    if ( ( p.l-1 != po.l ) || ( p.c != po.c ) ) {
      ps.l = p.l-1;
      ps.c = p.c;
      lng = lng+longueur(lb,p,ps); }
    if ( ( p.l+1 != po.l ) || ( p.c != po.c ) ) {
      ps.l = p.l+1;
      ps.c = p.c;
      lng = lng+longueur(lb,p,ps); }
    if ( ( p.l != po.l ) || ( p.c-1 != po.c ) ) {
      ps.l = p.l;
      ps.c = p.c-1;
      lng = lng+longueur(lb,p,ps); }
    if ( ( p.l != po.l ) || ( p.c+1 != po.c ) ) {
      ps.l = p.l;
      ps.c = p.c+1;
      lng = lng+longueur(lb,p,ps); } }
  return lng;
}

/* Fonction recursive de calcul de la distance */
/* maximale aux noeuds terminaux               */
/* d'un labyrinthe                             */

static int distanceMax(boolean [][] lb,int lo,int co,int l,int c) {
  int dst = 0;
  int dtf;
  int dMax = 0;
  if ( lb[l][c] ) {
    if ( ( l-1 != lo ) || ( c != co ) ) {
      dtf = distanceMax(lb,l,c,l-1,c);
      if ( dtf > dMax ) {
        dMax = dtf; } }
    if ( ( l+1 != lo ) || ( c != co ) ) {
      dtf = distanceMax(lb,l,c,l+1,c);
      if ( dtf > dMax ) {
        dMax = dtf; } }
    if ( ( l != lo ) || ( c-1 != co ) ) {
      dtf = distanceMax(lb,l,c,l,c-1);
      if ( dtf > dMax ) {
        dMax = dtf; } }
    if ( ( l != lo ) || ( c+1 != co ) ) {
      dtf = distanceMax(lb,l,c,l,c+1);
      if ( dtf > dMax ) {
        dMax = dtf; } }
    dst = 1+dMax; }
  return dst;
}

/* Recherche du nombre de voisins a vrai       */
/* d'une cellule                               */

static int nombreVoisins(boolean [][] lb,int l,int c) {
  int res = 0;
  if ( lb[l+1][c] )
    res++;
  if ( lb[l-1][c] )
    res++;
  if ( lb[l][c-1] )
    res++;
  if ( lb[l][c+1] )
    res++;
  return res;
}

/* Fonction recursive de recherche             */
/* des cellules terminales d'un labyrinthe     */

static void rechercheCellulesTerminales(boolean [][] lb,int lo,int co,int l,int c) {
  if ( lb[l][c] ) {
    if ( nombreVoisins(lb,l,c) == 1 ) {
      Ecran.afficherln(l," ",c); }
      else {
      if ( ( l-1 != lo ) || ( c != co ) ) {
        rechercheCellulesTerminales(lb,l,c,l-1,c); }
      if ( ( l+1 != lo ) || ( c != co ) ) {
        rechercheCellulesTerminales(lb,l,c,l+1,c); }
      if ( ( l != lo ) || ( c-1 != co ) ) {
        rechercheCellulesTerminales(lb,l,c,l,c-1); }
      if ( ( l != lo ) || ( c+1 != co ) ) {
        rechercheCellulesTerminales(lb,l,c,l,c+1); } } }
}

/* Fonction recursive de recherche             */
/* des cellules terminales d'un labyrinthe     */

static int elongation(boolean [][] lb,int lo,int co,int l,int c,int max) {
  int res = max;
  int v;
  if ( lb[l][c] ) {
    if ( nombreVoisins(lb,l,c) == 1 ) {
      v = distanceMax(lb,-1,-1,l,c);
      if ( v > res )
        res = v; }
      else {
      if ( ( l-1 != lo ) || ( c != co ) ) {
        v = elongation(lb,l,c,l-1,c,res);
        if ( v > res )
          res = v; }
      if ( ( l+1 != lo ) || ( c != co ) ) {
        v = elongation(lb,l,c,l+1,c,res);
        if ( v > res )
          res = v; }
      if ( ( l != lo ) || ( c-1 != co ) ) {
        v = elongation(lb,l,c,l,c-1,res);
        if ( v > res )
          res = v; }
      if ( ( l != lo ) || ( c+1 != co ) ) {
        v = elongation(lb,l,c,l,c+1,res);
        if ( v > res )
          res = v; } } }
  return res;
}

/* Amorcage du parcours d'un labyrinthe        */

static void parcours(boolean [][] lb,int l,int c) {
  parcours(lb,-1,-1,l,c);
}

/* Amorcage du calcul de la longueur           */
/* d'un labyrinthe                             */

static int longueur(boolean [][] lb,Position p) {
  Position po = new Position();
  return longueur(lb,po,p);
}

/* Amorcage du calcul de la distance maximale  */
/* aux noeuds terminaux d'un labyrinthe        */

static int distanceMax(boolean [][] lb,Position p) {
  return distanceMax(lb,-1,-1,p.l,p.c);
}

/* Amorcage de la recherche des cellules       */
/* terminales d'un labyrinthe                  */

static void rechercheCellulesTerminales(boolean [][] lb,Position p) {
  rechercheCellulesTerminales(lb,-1,-1,p.l,p.c);
}

/* Amorcage du calcul de l'elongation          */
/* d'un labyrinthe                             */

static int elongation(boolean [][] lb,Position p) {
  return elongation(lb,-1,-1,p.l,p.c,0);
}

/* Generation d'un nombre entier par tirage    */
/* au sort entre 1 et n inclus                 */
static int nombreAleatoire(int n) {
  return(1+(int)(Math.random()*n));
}

/* Creation d'un nouveau labyrinthe            */
/* par generation aleatoire                    */

static boolean [][] nouveauLabyrinthe(int nl,int nc) {
  boolean [][] lb = new boolean[nl][nc];
  int l = nombreAleatoire(nl-2);
  int c = nombreAleatoire(nc-2);
  int cpt = 1;
  lb[l][c] = true;
  while ( cpt < (nl-2)*(nc-2)/2 ) {
    l = nombreAleatoire(nl-2);
    c = nombreAleatoire(nc-2);
    if ( !lb[l][c] && ( nombreVoisins(lb,l,c) == 1 ) ) {
      cpt++;
      lb[l][c] = true; } }
  Ecran.afficherln(cpt);
  return(lb);
}

/* Determination d'une position a vrai         */
/* d'un labyrinthe                             */

static Position trouvePositionDepart(boolean [][] lb) {
  Position p = new Position();
  do {
    p.l = nombreAleatoire(lb.length-2);
    p.c = nombreAleatoire(lb[0].length-2); }
  while ( !lb[p.l][p.c] );
  return(p);
}

Clavier.class - Ecran.class - Exemple d'exécution

Exercice n°3

On souhaite implanter une fonction permettant de calculer la chaine de caractères expansée sur n niveaux d'un caractère selon les règles suivantes:
- Le caractère initial ne peut être que 'a', 'b' ou 'c'.
- A chaque niveau, 'a' évolue en "bc".
- A chaque niveau, 'b' évolue en "ca".
- A chaque niveau, 'c' évolue en "a".

Exemple: L'évolution du caractère 'a' donne "a", "bc", "caa", "abcbc","bccaacaa", "caaabcbcabcbc" aux étapes 0, 1, 2, 3, 4 et 5.

Expansion.java

/* Expansion d'un caractere en une chaine de caracteres   */
/* par substitution de lettres par d'autres lettres       */
/* a -> bc, b -> ca, c -> a                               */

public static String expansion(char lettre,int niveau) {
  String res = "";
  if ( niveau == 0 ) {
    res = res+lettre; }
    else {
    switch(lettre) {
      case 'a' :
        res = expansion('b',niveau-1)+expansion('c',niveau-1);
        break;
      case 'b' :
        res = expansion('c',niveau-1)+expansion('a',niveau-1);
        break;
      case 'c' :
        res = expansion('a',niveau-1);
        break; } }
  return res;
}

Clavier.class - Ecran.class - Exemple d'exécution

Exercice n°4

On souhaite implanter une fonction d'affichage du flocon de Koch au niveau 1. Le flocon de Koch est une courbe fractale obtenue par transformation récursive d'un segment de droite en 4 segments de droite selon le schéma ci-dessous.

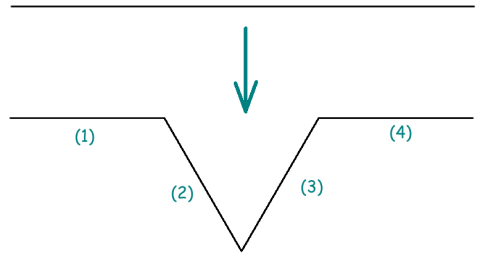
Le sous-segment (1) correspond au premier tier du segment initial. Le sous-segment (4) correspond au troisième tier du segment initial. Les sous-segments (2) et (3) remplacent le tier central tc du segment initial. Ils correspondent aux 2 autres cotés du triangle équilatéral dont tc est un des cotés. Ainsi du niveau 0 au niveau 4, les images suivantes sont obtenues.

Flocon.java

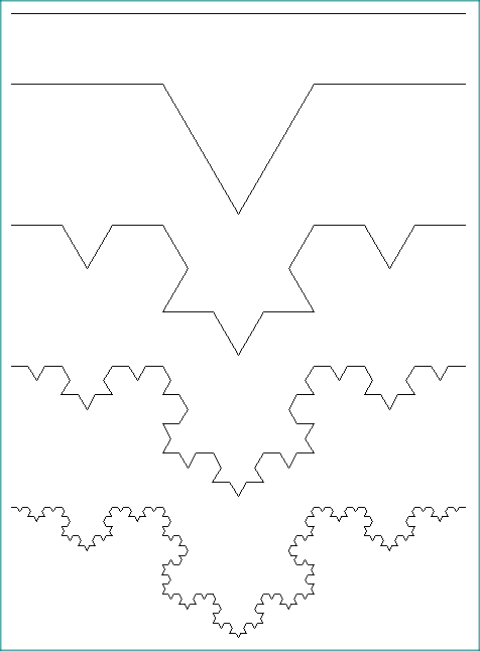
/* Type structure de stockage                   */
/* d'un segment de droite a coordonnees reelles */

static class Segment {
  double xi = 0.0;
  double yi = 0.0;
  double xf = 0.0;
  double yf = 0.0; };

/* Calcul et affichage d'un flocon de Koch      */

public static void flocon(Segment s,int niveau) {
  Segment s1 = new Segment();
  Segment s2 = new Segment();
  Segment s3 = new Segment();
  Segment s4 = new Segment();
  double dx;
  double dy;
  if ( niveau == 0 ) {
    EcranGraphique.drawLine((int) s.xi,(int) s.yi,
                            (int) s.xf,(int) s.yf); }
    else {
    dx = (s.xf-s.xi)/3.0;
    dy = (s.yf-s.yi)/3.0;
    s1.xi = s.xi;
    s1.yi = s.yi;
    s1.xf = s.xi+dx;
    s1.yf = s.yi+dy;
    flocon(s1,niveau-1);
    s2.xi = s1.xf;
    s2.yi = s1.yf;
    s2.xf = s2.xi+(dx-Math.sqrt(3.0)*dy)/2.0;
    s2.yf = s2.yi+(dy+Math.sqrt(3.0)*dx)/2.0;
    flocon(s2,niveau-1);
    s3.xi = s2.xf;
    s3.yi = s2.yf;
    s3.xf = s.xf-dx;
    s3.yf = s.yf-dy;
    flocon(s3,niveau-1);
    s4.xi = s3.xf;
    s4.yi = s3.yf;
    s4.xf = s.xf;
    s4.yf = s.yf;
    flocon(s4,niveau-1); }
}

Clavier.class - Ecran.class - Exemple d'exécution