Sujets et Exercices
de TD et TP
OpenGL, fonctions basiques pour la modélisation
Auxiliary library d'OpenGL
Programmation au moyen de fonctions C
Animations
Dernière modification
16/11/09 07:03:33
TD 1: Les fichiers VRML
Programmer les scènes suivantes:
Scène (1): Quartes cubes de coté 1.0 aux positions (1.5,0.0,1.5), (1.5,0.0,-1.5), (-1.5,0.0,1.5), (-1.5,0.0,-1.5).
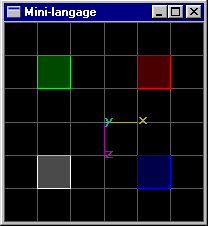
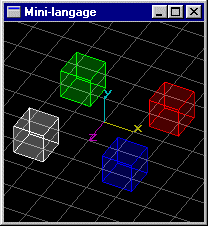
Scène (2): Même scène que précédemment, mais le cube de position (1.5,0.0,1.5) subit une rotation de 45° autour de l'axe y passant par son centre.
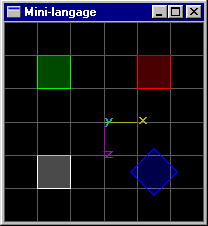
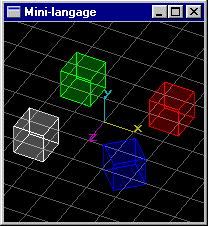
Scène (3): Même scène que précédemment, mais le cube de position (-1.5,0.0,1.5) possède une dimension en z égale à 2.
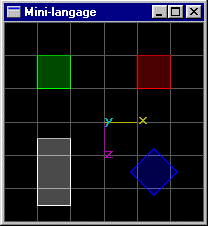
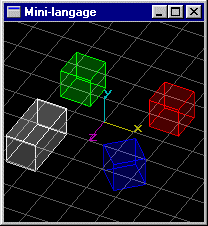
Scène (4): Même scène que précédemment, mais le cube de position (-1.5,0.0,-1.5) subit une rotation de 40° autour de l'axe y passant par son centre et une dimension en z égale à 2.
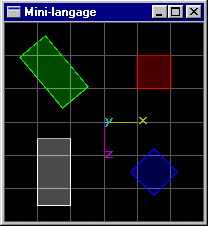
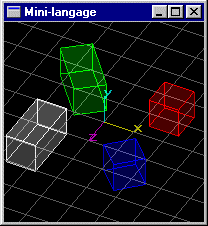
Scène (5): Même scène que la scène (3), mais le cube de position (-1.5,0.0,-1.5) subit une rotation de 30° autour de l'axe y passant par le centre de sa base de z maximum.
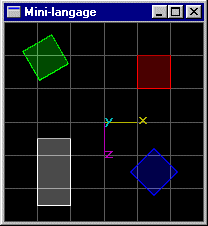
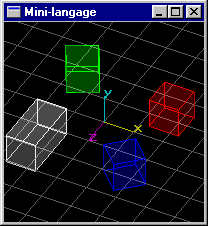
On se donne les instructions mini-langage supplémentaires suivantes:
Push pour l'empilement du repère courant
Pop pour le dépilement vers le repère courant du repère situé en haut de la pile de repères
Réécrire la scène (5) en exploitant ces deux nouvelles instructions et en rendant les objets indépendants les uns des autres.
Programmer la scène (6) suivante:
Un bras robot compose d'un avant-bras, d'un bras, et d'une paire de pinces. L'avant bras est articulé pour tourner autour de l'axe y d'un angle r1. Il s'agit d'un parallélépipède rectangle de dimension (3,1,1) (rouge). Le bras est articulé autour de l'axe y au bout de l'avant bras pour un angle r2. Il s'agit d'un parallélépipède rectangle de dimension (3,0.8,0.8) (vert). La pince est située au bout du bras. Elle peut tourner autour de l'axe du bras pour un angle r3. Le montant de la paire de pinces est un parallélépipède rectangle de dimension (0.6,1.2,1.8) (bleu). Chacune des mâchoires est un parallélépipède rectangle de dimension (1.0,1.2,0.4) (jaune) à même de se déplacer longitudinalement d'une valeur d pour réaliser une ouverture totale de 2xd.
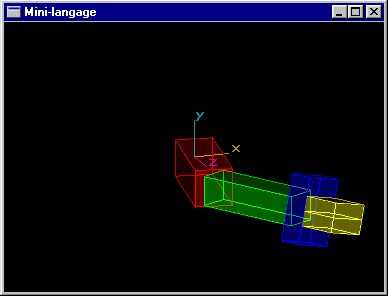
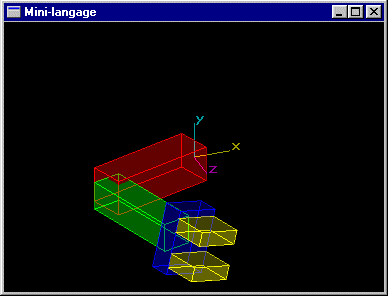

Solutions
| Solution scène (1) |
| Solution scène (2) |
| Solution scène (3) |
| Solution scène (4) |
| Solution scène (5) |
| Solution scène (5bis) |
| Solution scène (6) r1 = p/4, r2 = p/6, r3 = p/3, d = 0.2 |
TD 2: OpenGL pour le dessin de scènes
Fonctions à utiliser pour la modélisation d'une scène
Reprendre les scènes du TD précédent et les programmer en OpenGL.
Soit une scène composée de 3 parallélépipèdes rectangles posés les un sur les autres. Celui du bas est centré sur l'origine du repère et a pour dimensions (2,0.6,2), l'intermédiaire a pour dimension (1.2,3,1.2), le supérieur a pour dimension (2,0.4,2). Le repère est orienté avec x à droite, y en haut, et z vers l'observateur. Écrire une fonction C+OpengL modélisant cette scène.
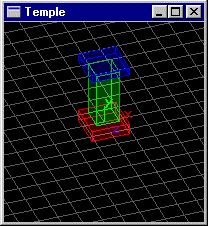
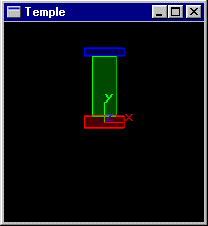
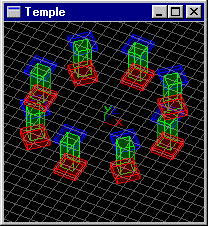
Soit une scène composée de n objets de l'exercice précédent répartis régulièrement sur un cercle de rayon 6 du plan xOz. Écrire une fonction C+OpenGL modélisant cette scène.
Soit la même scène modélisant un "temple" que l'on souhaite munir d'une frise composée de n parallélépipèdes rectangles placé au sommet des colonnes chacun en appui sur deux colonnes. Ces objets ont 2 pour taille en x et 0.4 pour taille en y. Écrire une fonction C+OpenGL modélisant cette scène.
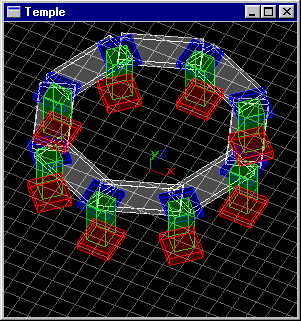
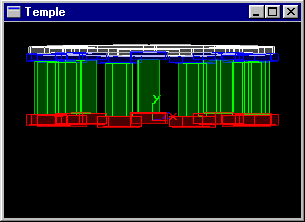
On s'efforcera d'écrire des fonctions C destinées à être utilisées au sein de fonctions display.
Solutions
Aux |
GLUt |
|||
| Les cubes | ||||
| Le bras robot | ||||
| Le temple | ||||
TD 3: L'Auxiliary library d'OpenGL
Programmation OpenGL au moyen de fonctions C
Réalisation d'animations
Programmer une animation pour une sphère S1 de rayon 2 tournant dans le plan xOy autour de O sur un cercle de rayon 4. L'animation est réalisée à raison de une image pour chaque degré de rotation -> 360 images pour un tour.
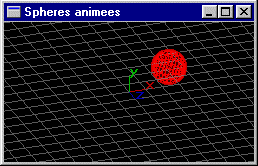
Reprendre l'animation précédente pour ajouter une sphère S2 de rayon 0.5 tournant dans le plan xOy autour de S1 sur un cercle de rayon 1. S2 tourne 5 fois plus vite que S1. L'animation est toujours réalisée à raison de une image pour chaque degré de rotation -> 360 images pour un tour de S1 -> 5 tours de S2.
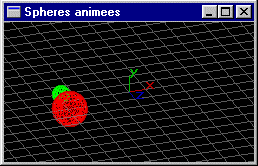
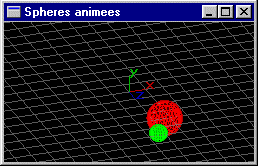
Reprendre l'animation précédente pour intégrer l'action de la touche de clavier Enter permettant d'interrompre l'animation et de la reprendre où elle avait été interrompue.
Programmer une scène composée d'une unique sphère de rayon 1.0 subissant des déformations suivant l'axe x la portant à la forme d'un ellipsoïde de demis grands axes 3.0, 1.0 et 1.0. Elle reste centrée sur l'origine.
L'animation est réalisée à raison de 50 images pour passer de 1.0 à 3.0, puis 50 images pour revenir à 1.0, et ainsi de suite cycliquement. Les déformations sont réalisées régulièrement.
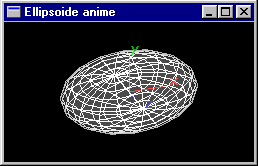
Reprendre l'animation précédente en intégrant une déformation selon l'axe y de rapport évoluant entre 1.0 et 3.0 sur 50+50 images. Elle prolongera le mouvement en x pour créer un cycle de 200 images.
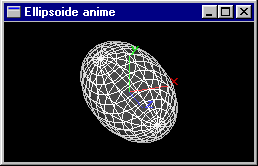
Solutions
On souhaite modéliser un cylindre de rayon r et de hauteur h centré sur l'origine.
Écrire une fonction OpenGL réalisant la génération de ce cylindre par calcul des positions des sommets des facettes et création de ces facettes.
Modifier la fonction précédente pour intégrer le calcul des normales aux sommets utilisées pour les calculs d'illumination.
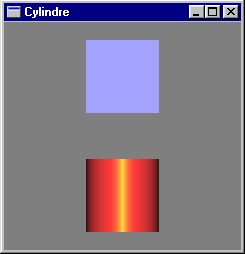

Solution
TD 5: La gestion des lumières en VRML et OpenGL
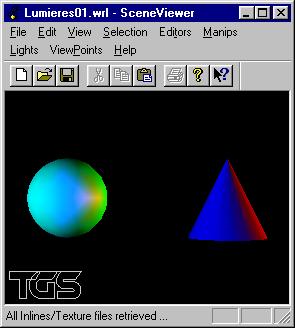
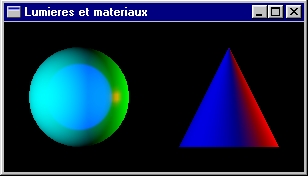
Soit une scène composée d'un cône de rayon 1 et de hauteur 2 placé en position (2.0, 0.0, 0.0) et d'une sphère de rayon 1 placée en position (-2.0, 0.0, 0.0). La sphère est diffusante dans le cyan et réfléchissante dans le rouge. Le cône est diffusant dans le magenta et non réfléchissant.
Ces deux objets sont éclairés par trois sources lumineuses:
- une source ponctuelle de couleur jaune placée en position (4.0, 0.0, O.0),
- une source directionnelle de couleur cyan orientée selon la direction (1.0, 0.0, -1.0).
- un spot de couleur bleue située en position (-2.0, 0.0, 5.0) éclairant selon l'axe -z avec 0.15 radians comme angle d'ouverture.
- Écrire le fichier VRML correspondant à cette scène.
|
|
|
Écrire le programme OpenGL correspondant à cette scène.
Solutions
Aux |
GLUt |
VRML |
||||
| Lumières et matériaux | ||||||
TD 6: Mathématiques pour l'Infographie: Outils élémentaires
Exercice 1
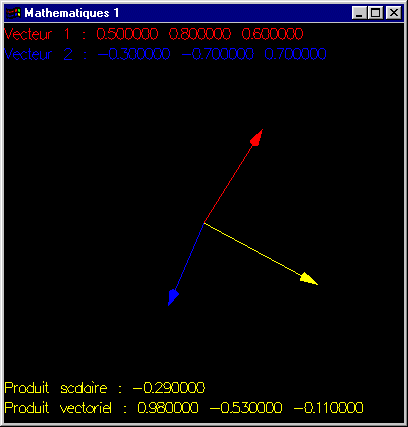
Soient deux vecteurs V1 et V2 de R3.
Définir une structure de données permettant de stocker un vecteur de R3 (Solution).
Ecrire une fonction calculant le produit scalaire de ces deux vecteurs (Solution).
Ecrire une fonction calculant le produit vectoriel de ces deux vecteurs (Solution).
Soit une facette triangulaire.
Ecrire une fonction calculant l'un des vecteurs normaux à cette facette (Solution).

Exercice 2
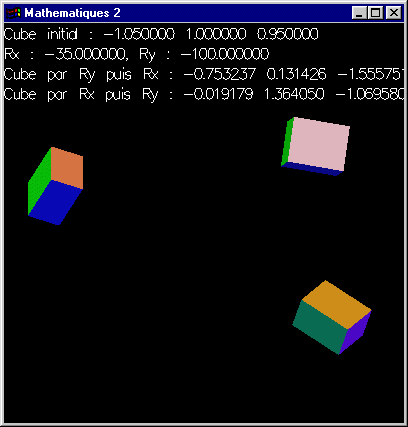
Soient les matrices de transformation canoniques Rx et Ry associées respectivement à la rotation par rapport à l'axe Ox et la rotation par rapport à l'axe Oy.
Calculer le produit matriciel Rx.Ry (Solution).
Calculer le produit matriciel Ry.Rx (Solution).
Établir la non commutativité du produit matriciel (Solution).
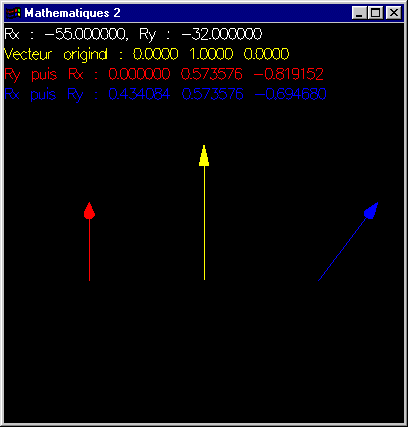
Établir lequel des deux produits matriciels est à même de conserver les verticales dans le cadre de l'implantation d'une transformation de visualisation où la verticale est donnée par l'axe Oy (Solution).
Solutions
GLUt |
||
| Stockage d'un vecteur | ||
| Produit scalaire | ||
| Produit vectoriel | ||
| Vecteur normal | ||
| Produit Rx par Ry | ||
| Produit Ry par Rx | ||
| Non commutativité | ||
| Conservation des verticales | ||
TD 7: Les lumières en Infographie: Modélisation mathématique par la formule de Lambert
Question 1: Définir une structure de données permettant de représenter une lumière directionnelle caractérisée par:
- une intensité,
- une couleur,
- une direction de propagation (Solution).Question 2: Définir une structure de données permettant de représenter un matériau du seul point de vue de la lumière diffuse (Solution)
Question 3: Ecrire une fonction calculant au moyen de la formule de Lambert la quantité d'énergie diffusée en chaque point d'une facette triangulaire plane éclairée par une source lumineuse directionnelle et affectée d'un matériau (Solution).
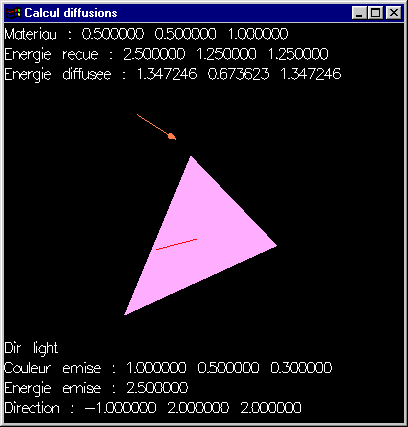
Question 4: Définir une structure de données permettant de représenter une lumière ponctuelle caractérisée par:
- une intensité,
- une couleur,
- une position (Solution).Question 5: Ecrire une fonction calculant au moyen de la formule de Lambert la quantité d'énergie diffusée en un point particulier d'une facette triangulaire plane éclairée par une source lumineuse ponctuelle et affectée d'un matériau. On ignorera l'atténuation de la lumière en fonction de la distance à la source d'émission (Solution).
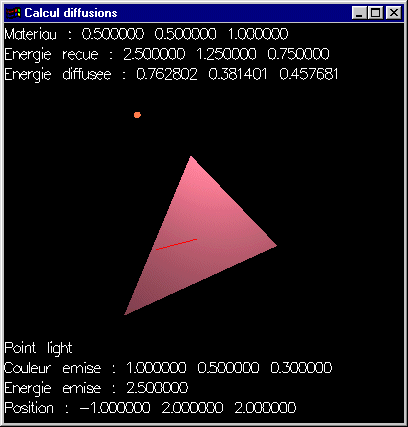
Question 6: Reprendre la fonction précédente pour intégrer un atténuation de la lumière reçue proportionnelle au carré de la distance à la source d'émission (Solution).
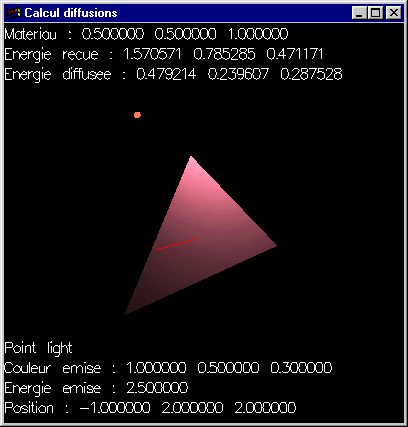
Solutions
GLUt |
||
| Structure lumière directionnelle | ||
| Structure matériau | ||
| Energie diffusée sur lumière directionnelle | ||
| Structure lumière ponctuelle | ||
| Energie diffusée sur lumière ponctuelle | ||
| Energie diffusée sur lumière ponctuelle avec atténuation | ||
TD 8: DEF, USE, WWWInline et WWWAnchor en VRML
Voir dans le cours l'utilisation de:
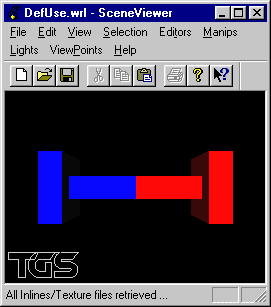
Soit une scène composée de 4 parallélipipèdes rectangles disposés en 2x2 objets le tailles (3, 1, 1) et (1, 3, 3) placés en positions centrées sur (1.5, 0, 0) et (3.5, 0, 0) pour le premier couplet et (-1.5, 0, 0) et (-3.5, 0, 0) pour le deuxième couplet.
Ecrire un fichier VRML modélisant cette scène en utilisant les opérateurs DEF et USE.
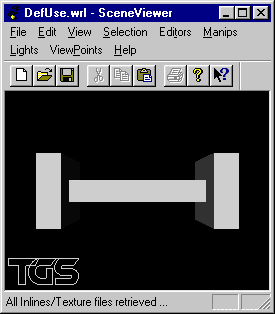
Reprendre le fichier précédent en définissant le premier couplet avec la couleur rouge et le second en bleu.
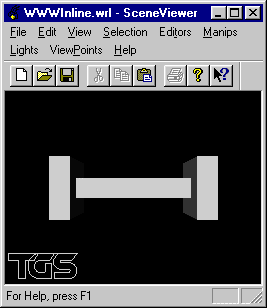
Ecrire deux fichiers VRML modélisant cette scène en utilisant le WWWInline.
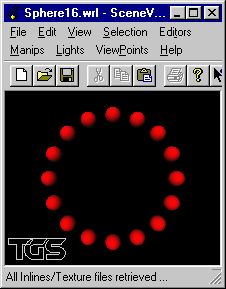
Soit la scène constituée de 16 sphères de rayon 2.5 placées régulièrement sur un cercle de rayon 20 centré sur l'origine et situé dans le plan xOy.
Ecrire les fichiers VRML modélisant cette scène en utilisant le WWWInline.
Solutions
TD 9: Le placage de texture en VRML et OpenGL
Voir dans les cours:
- le noeud VRML utilisé pour le plaçage de texture,
- les fonctions OpenGL utilisées pour le plaçage de texture
- Ecrire une fonction C générant un tableau de pixels à
même d'être utilisé comme paramètre dans la fonction de définition d'une texture 2D
en OpenGL.
Le motif est composé de 16 sur 16 pixels définissant un damier de 16 cases blanches et noires de 4x4 pixels chacune. Le tableau contient des valeurs RVB codées en octets.
- Ecrire un programme OpenGL utilisant cette fonction pour texturer un quadrilatère de coordonnées {(-4,1,-2), (2,4,3), (5,-1,-1), (-3,-2,4)} utilisant les coordonnées {(0,0), (0,2), (1,2), (1,0)} pour le placage de la texture.
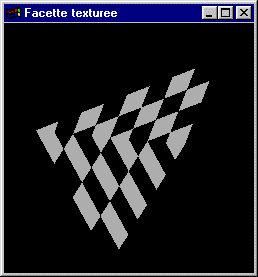
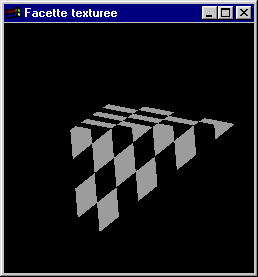
Solutions
GLUt |
||
| Les textures OpenGL | ||
![]()
TP 1-2: Conception
d'un programme C mettant en œuvre des instructions OpenGL
Écriture et visualisation de quelques fichiers VRML
Construction d'un projet VC++ autorisant la compilation d'instructions OpenGL par ajout des librairie OpenGL32.lib, Glu32.lib, Glaux.lib et Glut32.lib dans la liste des librairies utilisées au linkage.
Compilation et exécution de certains exemples du cours.
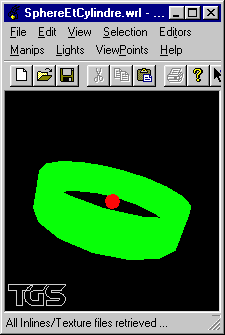
Écriture d'un programme OpenGL complet dessinant une scène composée d'une sphère de rayon 0.1 centrée sur l'origine et d'un cylindre de rayon 1.0, de hauteur 0.5 et centré sur l'origine, introduisant deux contrôles claviers permettant de tourner la scène autour de l'axe Ox et d'augmenter/réduire la hauteur du cylindre. Vérification des placement et orientation du cylindre.
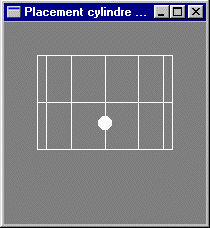
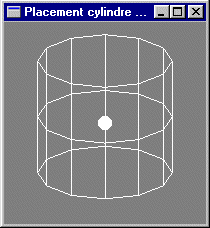
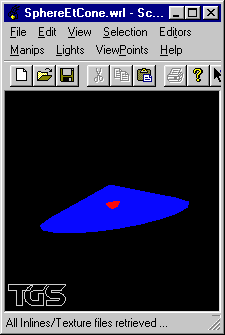
Modification du programme précédent pour dessiner un cône au lieu d'un cylindre. Vérification des placement et orientation du cône.
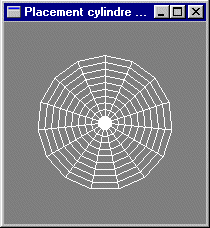
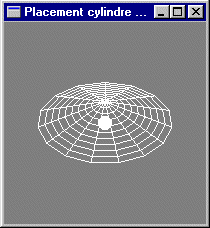
Lancement et utilisation des deux outils de visualisation de scène VRML: SceneViewer et CosmoPlayer.
Écriture de deux fichiers VRML correspondant aux scènes OpenGL précédentes.
Vérification des placement et orientation des cylindre et cône en VRML.
Solutions
Aux |
GLUt |
|||
| Structure lumière directionnelle | ||||
TP 3-4: Les caméras en VRML et en OpenGL
Soit la scène constituée d'une sphère, d'un cube, d'un cylindre et d'un cône placés respectivement centrés sur les positions (-3, 3, 0), (3, 3, 0), (3, -3, 0) et (-3, -3, 0).
Écrire un fichier VRML visualisant en gros plan la scène selon un point de vue placé en position (0, 0, 20) visant l'origine: axe de visée (0,0,-1).
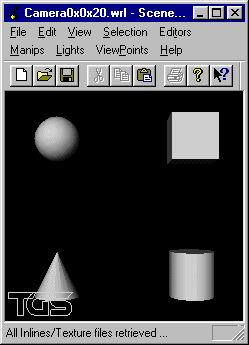
Écrire un fichier VRML visualisant en gros plan la scène selon un point de vue placé en position (20, 0, 0) visant l'origine: axe de visée (-1,0,0).
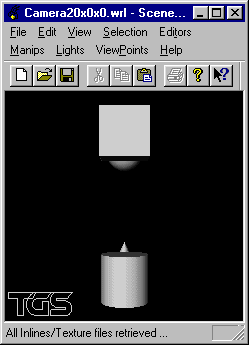
Écrire un fichier VRML visualisant en gros plan la scène selon un point de vue placé en position (0, 20, 0) visant l'origine: axe de visée (0,-1,0).

Écrire les fichiers VRML visualisant en gros plan la scène selon les points de vue (0, 20, 20), (20, 0, 20) et (20, 20, 0) visant l'origine: axe de visée (0,-1,-1), (-1,0,-1) et (-1,-1,0).
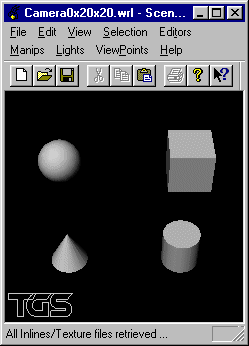
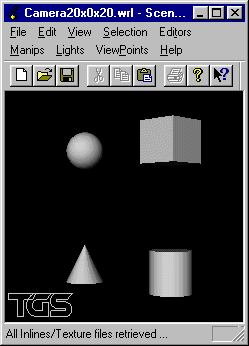
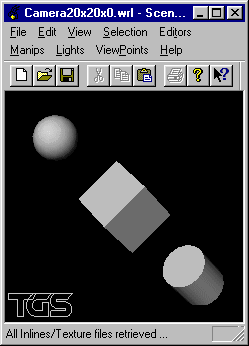
Écrire un fichier VRML visualisant en gros plan la scène selon un point de vue placé en position (20, 20, 20) visant l'origine: axe de visée (-1,-1,-1).
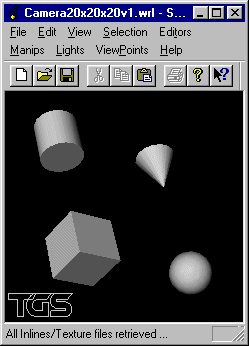
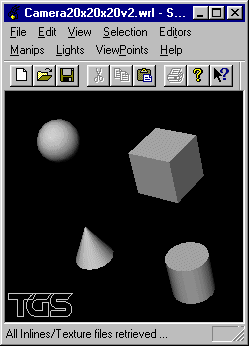
Reprendre les questions précédentes en les programmant en OpenGL et C au lieu de VRML.
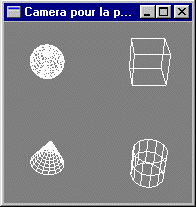
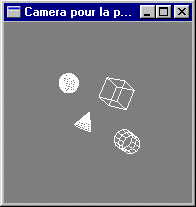
Solutions
VRML |
|||||||||
| Les fichiers VRML | |||||||||
Aux |
GLUt |
|||
| Le programme OpenGL | ||||
TP 5: Les lumières et matériaux en OpenGL
Soit la scène constituée d'une sphère
centrée sur l'origine et de deux lumières. Les caractéristiques de ces objets sont les
suivantes:
- La sphère est diffusante et réfléchissante dans le blanc.
- La première lumière éclaire en diffusion dans le rouge et en spéculaire dans le
vert. Elle est directionnelle et est orientée selon l'axe -x.
- La première lumière éclaire en diffusion dans le bleu et en spéculaire dans le vert.
Elle est directionnelle et est orientée selon l'axe x.
Écrire un programme OpenGL affichant cette scène.
Écrire un second programme OpenGL animant cette scène par rotation des deux sources lumineuses autour de l'axe Oy tandis que la sphère reste immobile.
Écrire un dernier programme OpenGL tel que les sources lumineuses sont transformées en sources de type spot placées à deux rayons de la sphère et éclairant vers son centre. L'angle d'ouverture est choisi de manière à ce que la sphère ne soit pas entièrement éclairée. L'affichage reste animé.
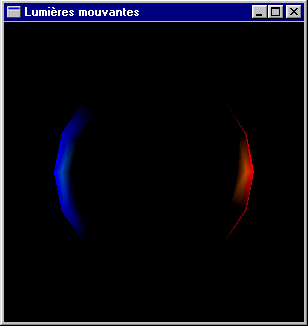



Solution
Aux + GLUt |
GLUt |
|||
| Le programme OpenGL | ||||
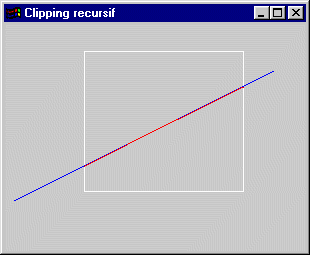
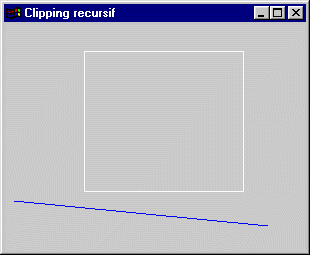
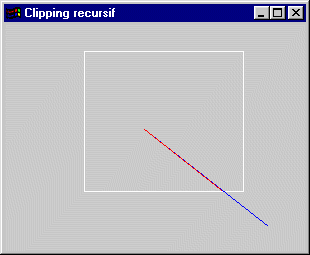
TP 6: Le clipping par une méthode dichotomique
Au moyen du codage employé dans la méthode de clipping de Cohen-Sutherland, on peut détecter qu'un segment rectiligne est intégralement dans un rectangle ou intégralement à l'extérieur d'un rectangle dans le seul cas où il est totalement au dessus, en dessous, à droite ou à gauche.
Écrire un programme permettant de clipper un segment de droite dans un rectangle. Le segment est défini par ses deux sommets extrémités.
La méthode employée sera dichotomique. C'est à dire que si le segment à clipper répond à l'un des deux cas précédemment énoncés, il est dessiné. S'il n'y répond pas, il est décomposé en deux sous-segments par séparation au niveau du point milieu entre les deux extrémités et l'algorithme est lancé récursivement sur chacun de ces deux sous-segments.
Solution
Aux |
GLUt |
|||
| Le programme OpenGL | ||||
TP7: Le dessin de segments par l'algorithme de Bresenham
L'algorithme de Bresenham est un
algorithme générique pour le tracé de segments de droites sur écran bitmap.
Les affichages demandés sont réalisés dans des fenêtres OpenGL où les pixels sont
matérialisés par des carrés de coté de dimension supérieure à 1 pixel (10 pixels par
exemple) de manière à mettre en évidence les pixels affichés et le fait qu'ils sont
bien dessinés par recouvrement du segment continu.
Écrire un programme d'implantation simple du tracé de segments de Bresenham.

Reprendre le programme précédent pour autoriser l'utilisation d'un motif de remplissage sur 16 bits où un 0 indique un pixel non tracé et un 1 indique un pixel effectivement tracé.

Modifier l'algorithme de Bresenham pour qu'il trace des segments en 4-connexité et non plus en 8 connexité.

Solution
Aux |
GLUt |
|||
| Le programme OpenGL | ||||
TP8: DEF, USE, WWWInline et WWWAnchor
Programmer les exercices du TD n°8.


