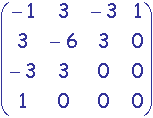Les courbes et
surfaces lissées
PARAMÉTRIQUES
CUBIQUES
Définition
Propriétés, applications
COURBES
DE BÉZIER
Définition
Propriétés
Algorithme
COURBES B-SPLINES
NON RATIONNELLES
UNIFORMES
Définition
Propriétés
Algorithme
SPLINES
DE CATMULL-ROM
Définition
Propriétés
B-SPLINES NON
RATIONNELLES UNIFORMES
SURFACES
PARAMÉTRIQUES
BICUBIQUES
Définition
Propriétés
QUADRIQUES
Définition
Exemples
1. Problèmatique
La modélisation par facettes se heurte au problème de la création des ensembles de facettes permettant de modéliser des objets élémentaires. En effet
il s'agit là d'une tâche possiblement difficile. Une solution algorithmique existe généralement pour les objets modélisables au moyen d'équations
mathématiques. Malheureusement, tous les objets ne sont pas modélisables au moyen d'équations mathématiques.
Une technique courament utilisée consiste à créer chacun des objets graphiques que l'on souhaite modéliser à partir d'un ensemble restreint
de sommets qui lui sera propre et qui sera employé pour générer les autres sommets nécessaires au moyen d'équations mathématiques spécifiques.
Ces sommets sont souvent nommés "points de contrôle" car leurs positions contrôlent la forme de l'objet obtenu.
|
Modélisation à base de sommets de contrôle : marqueurs jaunes et vert ci-dessous |
|
|
|
Touches de curseur pour changer la position du point de contrôle sélectionné (en vert) Espace pour switcher entre les points de contrôle |
Même si cela n'est pas obligatoire, les positions des sommets mathématiquement générés à partir des points de contrôle seront généralement telles
que la forme de la "structure" géométrique ainsi obtenue "lissera" la forme de la structure grossière formée des points de contrôle :
- une courbe lissée à partir d'une ligne polygonale,
- une surface lissée à partir d'un maillage (généralement quadrangulaire).
Ceci explique l'utilisation en informatique graphique de concepts mathématiques relatifs aux courbes lissés.
2. Les courbes paramétriques cubiques en 3D
Courbe paramétrique cubique Q de R3 (donc en 3D) : Courbe définie par le système d'équations paramétriques cubiques suivant :
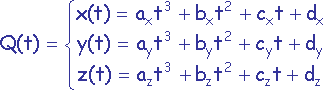
![]() (1)
(1)
Pour obtenir des segments de courbe, on considère que l'unique paramètre variable t appartient à un intervalle [min,max] (fréquemment [0.0,1.0]).
Reformulation matricielle
La formulation (1) est peu pratique pour la finalité qui est la notre. En effet, elle ne fait pas directement apparaître la notion de point de contrôle. Une reformulation matricielle permet de résoudre cette difficulté.
Soit le vecteur T = (t3, t2, t, 1.0).
Le système (1) s’écrit sous la forme Q(t) = (x(t), y(t), z(t)) = T.C avec C =
 et
et
![]() .
.
4 coefficients numériques constants sont nécessaires pour définir chacune des 3 équations paramétriques.
-> 4 contraintes mathématiques sont imposées pour définir l'équation selon chacun des 3 axes.
Pour faire "apparaître" des points de contrôle, on transforme la matrice C en la matrice produit M.G où M est une matrice 4x4 de valeurs
numériques réelles (appelée matrice de base) et G est une matrice 4x3 (appelé vecteur géométrie) de 4 contraintes géométriques : 4 points de
contrôles.
Les lignes de G sont donc occupées par les 3 coordonnées de chaque point de contrôle.
Q(t) = (x(t), y(t), z(t)) = T.C = T.M.G =
 (2)
(2)
La matrice G permet donc de représenter 4 contraintes géométriques s'appliquant à la courbe qui s'apparenteront à la position de 4 points dans l'espace de représentation. La courbe générée évoluera "entre" ces 4 points.
La matrice M permet d'attribuer des "poids" respectifs à chacun des coefficients ti s’appliquant à une contrainte géométrique, permettant ainsi de définir la "forme" de la courbe.
De bons choix de matrice M permettront d'obtenir des tracés de courbe approximant la ligne polygonale à 4 sommets définie par les 4 points de contrôle.
Différents choix permettront d'obtenir des tracés présentant différentes caractéristiques.
|
Trois types de courbes paramétriques cubiques obtenus par paramétrage de la matrice M |
|
|
|
|
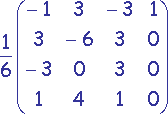 |
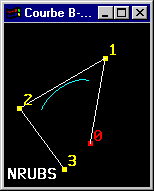 |
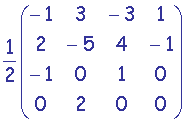 |
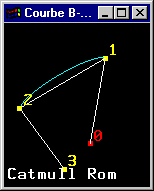
|
|
Enter pour switcher entre des affichages utilisant |
|
Les courbes de cette famille ont pour propriétés d'être:
- continues,
- de dérivés premières en t continues (dérivation en t de chaque composante de T pour obtenir T'= (3.0*t2, 2.0*t, 1.0, 0.0)),
- de dérivés secondes en t continues (double dérivation en t de chaque composante de T pour obtenir T" = (6.0*t, 2.0, 0.0, 0.0)).
Il sera donc possible de calculer la tangente à la courbe en un point défini par la valeur t (pour le vecteur T = (t3, t2,
t, 1.0)) en appliquant la formule de calcul (2), mais pour le vecteur T' = (3.0*t2, 2.0*t, 1.0, 0.0).
| Tangente à une courbe paramétrique cubique |
|
|
|
Enter pour switcher entre des affichages utilisant |
En pratique
D'un point de vue pratique, générer une courbe paramétrique cubique nécessitera de :
- définir la position des 4 points de contrôle (définir la matrice G),
- choisir la matrice base (la matrice M) correspondant au résultat souhaité,
- choisir le nombre n de points à générer,
- choisir l'intervalle de variabilité [ti,tf] à utiliser pour t (cet intervalle est très généralement [0.0,1.0]),
- calculer n valeurs t uniformément réparties entre ti et tf,
- trouver la position de chacun des n points de la courbe en appliquant la formule de calcul (2) pour chaque valeur de t calculée ci-dessus.
Les propriétés de continuité, de continues dérivabilités première et seconde sont primordiales car elles assurent la possibilité de se déplacer uniformément
sur tous les points de la courbe. Elles assurent aussi que, quand on fait varier t uniformément, la vitesse de déplacement est continue (pas de déplacement
instantané) et l'accélération du déplacement est continue (pas de saute de vitesse instantanée).
Géométriquement, ces propriétés nous assurent que ces courbes n'ont pas de trou et ne présentent pas de rupture dans l'orientation des tangentes
c'est à dire qu'elles sont bien courbes (non brisées) et donc sans changement de direction instantané.
Les courbes paramétriques cubiques ne sont pas déformées par transformation géométrique de type translation, rotation, zoom (ou composition de ces
types de transformation, donc par exemple projection parallèle orthographique) de leurs points de contrôle. En revanche, elles sont modifiées si
on souhaite faire une transformation de type mise en perspective.
Cette propriété signifie que si on doit par exemple effectuer une transformation géométrique M sur une courbe paramétrique cubique Q définie à partir
des points de contrôle G1, G2, G3, et G4 de façon à générer n points, alors M(Q(n,G1,G2,G3,G4))
= Q(n,M(G1),M(G2),M(G3),M(G4)) si M est d'un des types possibles définis ci-dessus.
Pourquoi est-il beaucoup plus efficace de calculer selon le terme droit ? Solution
Problèmatique : Les courbes paramétriques cubiques sont définies sur 4 points de contrôle. Que faire si on en a moins (3 points) ou plus (5, 6, 7 points ou encore plus) ?
P0, P1, P2, P3, ..., Pn sont les n+1 points définissant une ligne polygonale (n > 1). La
courbe de Bézier définie par ces points est défnie par l'équation paramétrique de degré n suivante :
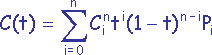 avec t ∈ [0.0,1.0].
(3)
avec t ∈ [0.0,1.0].
(3)
On rappelle que
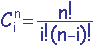 .
.
Telle qu'elle est formulée, cette équation fait référence aux point Pi. En 3D, elle s'implante sous la forme de trois équations :
une équation x(t) qui reprend les coordonnées x des Pi, une équation y(t) qui reprend les coordonnées y des Pi, une équation
z(t) qui reprend les coordonnées z des Pi. L'équation (3) est donc utilisée 3 fois.
On a donc C(t) = (x(t), y(t), z(t)).
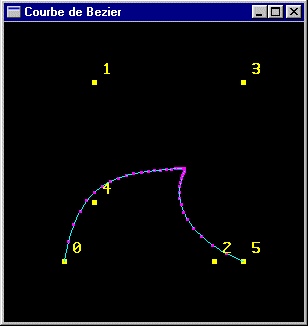
|
Une courbe de Bézier construite sur un nombre arbitraire de sommets En cyan la courbe générée en utilisant l'implantation OpenGL de calcul des courbes de Bézier En magenta la courbe obtenue par notre implantation de la formule |
|
|
|
Enter pour switcher entre 2, 3, 4, 5 et 6 points |
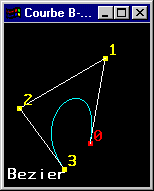
Une courbe de Bézier
- commence par le premier point de contrôle, finit par le dernier point de contrôle et ne passe pas généralement par les autres points de
contrôle,
- est tangente au segment P0,P1 en P0 et au segment Pn,Pn-1 en Pn,
- n'est pas déformée par translation, rotation, zoom et composition de ces transformations,
- est déformée par changement des paramètres de mise en perspective.
Problèmes
Temps de calcul :
- Quoique pouvant être optimisé, le calcul des Cin n'est pas économique en temps.
- Les deux mises à la puissance en t et en 1-t ne sont pas économiques en temps.
Aptitude à assurer une fonction d'outil de modélisation :
- La courbe est intégralement modifiée quand on modifie la position d'un seul point de contrôle. Ceci a pour conséquence l'obligation
de la réévaluer intégralement. Il n'y a donc pas de contrôle local sur la forme de la courbe.
- Lorsqu'une courbe de Bézier est tracée avec beaucoup de sommets, les sommets intermédiaires sont peu "attractifs". La courbe
reste donc loin d'eux. Il n'y a donc pas de fort contrôle de la forme de la courbe.
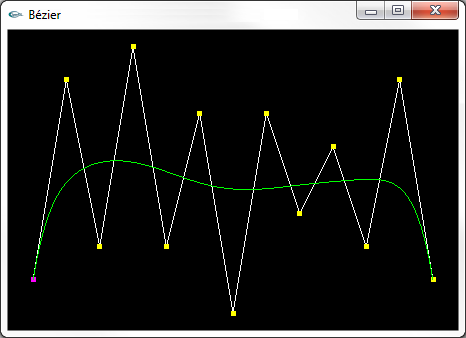
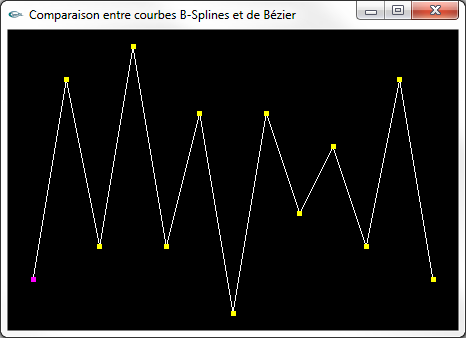
|
Une courbe de Bézier construite sur une ligne polygonale de 13 points de contrôle |
|
|
|
Espace pour changer de sommet sélectionné (en magenta) |
Algorithme (langage C)
Précision : Le calcul des Cin est prétraité dans un tableau de façon à en optimiser le temps de calcul global.
struct coord_3D {
GLfloat x = 0.0F;
GLfloat y = 0.0F;
GLfloat z = 0.0F;
GLfloat w = 1.0F; };
struct lignePolygonale {
int n = 0;
coord_3D *p = NULL; };
void point(float x,float y,float z) {
glVertex3f(x,y,z);
}
/* Trace la courbe de Bezier formee de n points */
/* generee a partir de la ligne polygonale p */
void bezier(lignePolygonale *p,int n) {
float x,y,z;
float *cn =(float *) calloc(p->n,sizeof(float));
cn[0] = 1;
cn[1] =(float) (p->n-1);
for ( int i = 2 ; i < p->n ; i++ )
cn[i] = cn[i-1] * (p->n - i) / i;
for ( int i = 0 ; i < n ; i++ ) {
float t =(float) i/(n-1);
float mt = 1.0F-t;
x = y = z = 0.0F;
for ( int j = 0 ; j < p->n ; j++ ) {
float fac = cn[j]*(float) pow(t,j)*
(float)
pow(mt,p->n-1-j);
x += fac * p->p[j].x;
y += fac * p->p[j].y;
z += fac * p->p[j].z; }
point(x,y,z); }
free(cn);
}
Cas particulier
Si n = 3 (4 sommets), C(t) peut être présentée sous la forme d'une courbe paramétrique cubique définie par les 4 points de contrôle P0, P1, P2, P3. Les 4 contraintes géométriques G1, G2, G3 et G4 sont alors les positions de ces 4 points de contrôle.
On a alors:
C(t) = (x(t), y(t), z(t)) =
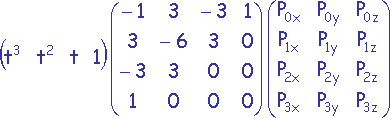
Problèmatique : Comment acquérir un contrôle local et obtenir un bon lissage avec beaucoup de points de contrôle ?
Solution : Relier 2 courbes de Bézier définies sur 4 sommets tels que le dernier sommet définissant la première courbe soit confondu avec le premier sommet de la seconde. C'est à dire tracer la courbe Pi avec 0 <= i <= 6 (soit au total 7 sommets différents).
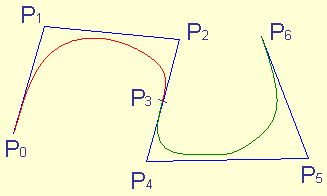
Assemblage de 2 courbes de Bézier
Les conditions suivantes doivent être respectées pour que les propriétés de continues dérivabilités première et seconde souhaitées soient obtenues
au point P3 qui est le point problématique :
- Si P2, P3 et P4 sont sur la même droite alors il y a continue dérivabilité au point P3.
- Si les distances entre P2 et P3 d'une part et P3 et P4 d'autre part sont identiques
alors il y a continue dérivabilité seconde au point P3.
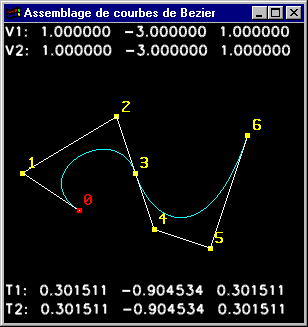
|
Une courbe construite par assemblage de 2 courbes de Bézier à 4 points de contrôle |
|
|
|
Espace pour changer de sommet |
Avantages
- On dispose d'un contrôle local.
- La courbe est "bien" lissée et contrôlée.
- Il est possible d'ajouter des points de contrôle.
Inconvénient
- Tous les points de contrôle ne sont pas "au même niveau". Il y a les points partagés et les autres.
- Le nombre de points de contrôle peut dépasser 4 mais il n'est pas totalement libre car il est égal à 1+3*n où n est le nombre de morceaux
de Bézier dessinés.
- A cause des contraintes géométriques indiquées ci-dessus les points de contrôle ne sont pas indépendants les uns des autres.
Application
- Tracé de courbes lissées quand le nombre de points de contrôle n'est pas fortement imposé
-> Utilisation dans les logiciels de dessin vectoriel et de modélisation géométrique
4. Les courbes B-Splines (splines non rationnelles uniformes)
Problèmatique : Comment lisser une ligne polygonale quelconque de telle façon que la modification de la position d'un seul
sommet ne modifie pas l'intégralité de la courbe et que l'on ait une bonne capacité de lissage, c'est à dire que la courbe soit assez
attirée par les points de contrôle ?
-> En cas de modification de la position d'un point de contrôle, seule une partie limitée de la courbe lissée aura à être recalculée.
P0, P1, P2, P3, ..., Pn-1 sont les n points définissant une ligne polygonale P (n >= 4, 0 <= i < n).
Les n points de P permettent de définir les n-3 vecteurs géométriques Gi =
![]() avec 0 <= i
< n-3.
avec 0 <= i
< n-3.
Ces n-3 vecteurs géométriques permettent la génération de n-3 morceaux de courbe paramétrique cubique
calculés sur l'intervalle de variabilité [0.0,1.0] pour t (variation uniforme sur cet intervalle) en utilisant la matrice de base
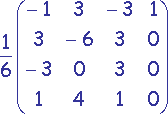 . Ces morceaux sont jointifs (voir preuve ci-dessous). Une
fois réunis ils formeront une courbe lissée approximant la ligne polygonale P. A toutes les jointures les dérivées première et seconde sont égales
(preuve non fournie ici mais dérivée de celle de la continuité).
. Ces morceaux sont jointifs (voir preuve ci-dessous). Une
fois réunis ils formeront une courbe lissée approximant la ligne polygonale P. A toutes les jointures les dérivées première et seconde sont égales
(preuve non fournie ici mais dérivée de celle de la continuité).
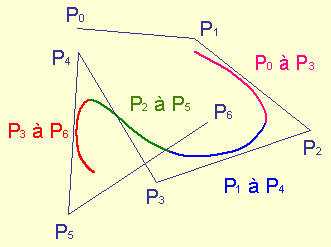
Assemblage de morceaux de courbe
pour construire une courbe B-Spline
Continuité des B-Splines
Les morceaux de courbe B-Spline se joignent obligatoirement en leurs extrémités. En effet, soient les deux morceaux de courbe correspondant à Gi
et Gi+1, le premier se finit à t = 1.0, le second commence à t = 0.0. En ces points, on calcule que les coordonnées obtenues sont identiques
et ont pour valeur
![]() . Cette position est quelque part à l'intérieur du triangle
défini par les trois sommets, plus proche de PPi+2 que des 2 autres car il s'agit du barycentre des points Pi+1, Pi+2
et pi+3 respectivement affectés des poids 1.0, 4.0 et 1.0.
. Cette position est quelque part à l'intérieur du triangle
défini par les trois sommets, plus proche de PPi+2 que des 2 autres car il s'agit du barycentre des points Pi+1, Pi+2
et pi+3 respectivement affectés des poids 1.0, 4.0 et 1.0.
Contrôle local
Chaque morceau de courbe dépend de 4 points de contrôle. Chaque point de contrôle intervient sur au maximum 4 morceaux de courbe.
-> On n'a pas l'obligation de recalculer toute la courbe si un seul point est modifié, mais seulement 4 morceaux au maximum.
Attractivité des points de contrôle
La preuve de continuité a déterminé que les points de jointure sont situés dans les triangles (Pi+11,Pi+2, pi+3) et, dans ces triangles, assez attirés par les points Pi+22, (poids 4.0 pour ce point, 1.0 pour les deux autres). Les points de contrôle attirent donc assez fortement la courbe générée.
Les courbes B-Splines NRU :
- ne passent pas par les sommets de la ligne polygonale maîtresse, y compris le premier et le dernier,
- respectent la continuité, la continue dérivabilité première et la continue dérivabilité seconde.
Une solution simple pour passer par le premier et le dernier point consiste à tripler ces points.
Algorithme (langage C)
struct coord_3D {
GLfloat x = 0.0F;
GLfloat y = 0.0F;
GLfloat z = 0.0F;
GLfloat w = 1.0F; };
struct lignePolygonale {
int n = 0;
coord_3D *p = NULL; };
typedef float matrice[4][4] ;
void point(float x,float y,float z) {
glVertex3f(x,y,z);
}
/* Trace un morceau de courbe B-Spline */
/* p est le tableau des 4 points de controle */
/* n est le nombre de points generes */
/* m est la matrice de base utilisee */
void morceauBSpline(coord_3D *p,int n,matrice m) {
float tt[4],ttt[4],x,y,z ;
for ( int i = 0 ; i < n ; i++ ) {
float t =(float) i/(n-1) ;
tt[0] = t*t*t ;
tt[1] = t*t ;
tt[2] = t ;
tt[3] = 1.0F ;
for ( int j = 0 ; j < 4 ; j++ ) {
ttt[j] = 0.0F ;
for ( int k = 0 ; k < 4 ; k++ )
ttt[j] += tt[k] * m[k][j] ; }
x = y = z = 0.0F ;
for ( int j = 0 ; j < 4 ; j++ ) {
x += ttt[j] * p[j].x ;
y += ttt[j] * p[j].y ;
z += ttt[j] * p[j].z ; }
point(x,y,z) ; }
}
/* Trace une courbe B-Spline par morceaux */
/* m est la matrice de base utilisee */
/* p est la ligne polygonale lissee */
/* n est le nombre de points generes sur chacun */
/* des p->n-3 morceau traces
*/
/* ATTENTION : Les points de rattachement */
/* des morceaux de B-Spline sont generes deux fois. */
void BSpline(lignePolygonale *p,matrice m,int n) {
for ( int i = 0 ; i < p->n-3 ; i++ )
morceauBSpline(&p->p[i],n,m) ;
} }
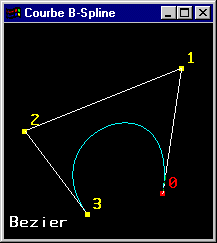
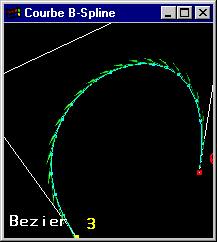
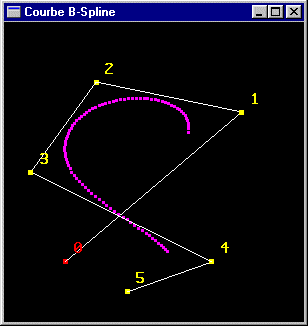
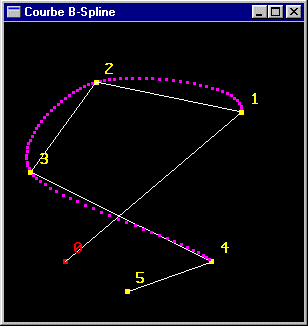
|
Une courbe B-Spline NRU construite sur 6 points de contrôle |
|
|
|
Enter pour switcher entre des affichages |
5. Les courbes Splines de Catmull-Rom
Problèmatique : Comment lisser une ligne polygonale par une courbe paramétrique cubique passant par chacun des sommets de cette
ligne.
-> Utilisation des courbes Splines de Catmull-Rom.
P0, P1, P2, P3, ..., Pn-1 sont les n points définissant une ligne polygonale P (n >= 4, 0 <= i < n).
On définit les n-3 vecteurs géométriques Gi =
![]() avec 0 <= i < n-3.
avec 0 <= i < n-3.
La matrice de base utilisée pour la génération des morceaux de Spline est
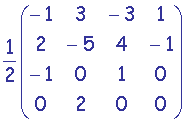 et l'intervalle de variabilité uniforme de t est [0.0,1.0].
et l'intervalle de variabilité uniforme de t est [0.0,1.0].
Pour le vecteur géométrique Gi, la courbe commence pour t = 0.0 en Pi+1, et finit pour t = 1.0 en Pi+2. Les morceaux se rejoignent bien et, de plus, ils se rejoignent au niveau des points de contrôle.
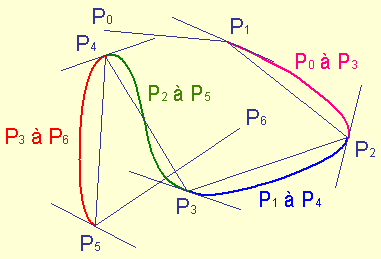
Assemblage de morceaux de courbe
pour construire une courbe Spline de Catmull-Rom
|
Une spline de Catmull-Romm construite sur 6 points de contrôle |
|
|
|
Enter pour switcher entre des affichages |
Les courbes splines ainsi définies :
- passent par tous les sommets de la ligne polygonale, à l'exception du premier et du dernier,
- commencent au deuxième point et finissent à l'avant dernier point de la ligne polygonale maîtresse,
- sont tangentes au point Pi à la direction donnée par la droite passant par les points Pi-1 et Pi+1,
- respectent la continuité, les continues dérivabilités première et seconde.
Une solution simple pour passer par le premier et le dernier point consiste à doubler ces points.
6. Comparaison entre courbes lissées
Le programme ci-dessous présente l'affichage des trois types de courbe lissée présentés dans ce chapitre.
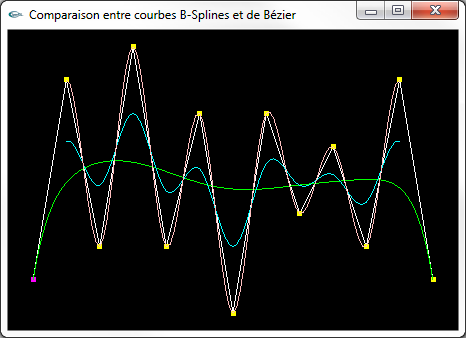
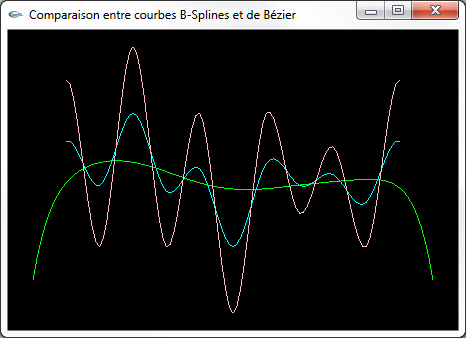
|
Courbes lissées construites sur une ligne polygonale de 13 points de contrôle Vert : Courbe de Bézier Cyan : Courbe B-Spline NRU Rose : Courbe spline de Catmull-Rom |
|
|
|
Espace pour changer de sommet sélectionné (en magenta) |
![]()
7. Les courbes B-Splines non uniformes rationnelles : les NURBS
Problématique : Une B-Spline non rationnelle est calculée au moyen de points de contrôle. Si elle est visualisée en perspective,
la même courbe devra être toujours être modélisée et affichée quels que soient les paramètres de mise en perspective. Or, il n'est pas possible
de placer les points de contrôle en perspective et de calculer la B-Spline ensuite. On devra d'abord calculer la B-Spline pour ensuite faire
la mise en perspective sur l'ensemble des points obtenus. Faute de cet ordre de manipulation, la B-Spline obtenue n'est pas invariante par
modification des paramètres de mise en perspective avec pour conséquence des problèmes de visualisation.
Cet ordre de calcul est inefficace en temps de calcul car le nombre de sommets de la courbe lissée est plus grand que le nombre de points de contrôle.
Solution : Utiliser les B-Splines non-uniformes rationnelles.
Définition mathématique
Courbe NURBS :
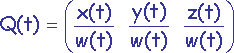 avec x(t), y(t), z(t) et w(t) des équations paramétriques cubiques représentant des coordonnées homogènes.
avec x(t), y(t), z(t) et w(t) des équations paramétriques cubiques représentant des coordonnées homogènes.
8. Les surfaces paramétriques bicubiques
Les surfaces paramétriques bicubiques sont une généralisation aux surfaces des courbes paramétriques cubiques.
Soit une courbe cubique Q(s) = S.M.G (s et S sont équivalents à t et T). Le vecteur géométrique G est constitué de composantes constantes. Si ces composantes sont remplacées par des courbes paramétriques cubiques, on obtient :
Q(s,t) = S.M.G(t) = S.M.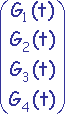 avec s et t compris dans l'intervalle [0.0,1.0].
avec s et t compris dans l'intervalle [0.0,1.0].
Les Gi sont des cubiques.
-> Gi(t) = T.M'.Pi avec Pi = (Pi1,Pi2,Pi3,Pi4)T
-> Gi(t) = (T.M'.Pi)T = PiT.M'T.TT
= (Pi1,Pi2,Pi3,Pi4).M'T.TT.
Précision : On utilise deux matrices de base M (celle de la courbe Q(s)) et M' (celle des courbes Gi(t)) car il n'est pas
obligatoire que Q(s) et les Gi(t) aient la même matrice de base.
Chaque point Pij est un point de contrôle de Gi(t).
-> On a au total 4x4 = 16 points de contrôle Pij
Reconstruite sous la forme d'une formule unique, on obtient :
Q(s,t) = S.M. .M'T avec s et t compris dans l'intervalle
[0.0,1.0].
.M'T avec s et t compris dans l'intervalle
[0.0,1.0].
La modification d'un seul des 16 points de contrôle entraîne la modification de l'ensemble de la surface.
Le choix des matrices M et M' permet d'adapter les caractéristiques de la surface modélisée aux spécifications désirées.
Ces matrices pourront être celles décrites précédemment dans le chapitre (Bézier, B-Spline NRU, Catmull-Rom) ou route autre matrice.
Elles pourront être identiques ou bien différentes l'une de l'autre pour obtenir certaines caractéristiques selon un axe et des caractéristiques
différentes selon l'autre axe.
Interprétation intuitive
Une interprétation intuitive consiste à considérer qu'une telle surface est générée à partir d'une matrice carrée de 4x4 points de contrôle. Les 4 lignes de 4 points de cette matrice permettent de générer 4 séries primaires de m points qui vont eux-mêmes être utilisés pour constituer m séries de 4 points de contrôle, chacune de ces m séries permettant de générer une serie secondaire de n points modélisant la surface lissée. Au total, on obtient donc un maillage quadrangulairede m*n points qui peut être utilisé pour généré des facettes.
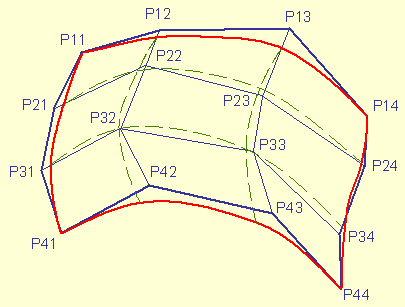
Organisation des 4x4 points de contrôle en un maillage quadrangulaire (en bleu)
Utilsation de ce maillage pour générer une surface paramétrique bicubique
(en vert et rouge pour le bord)
|
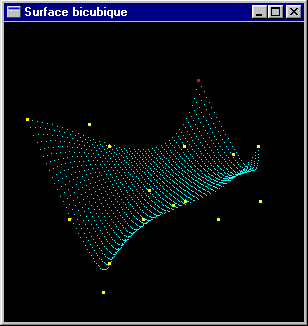
Une surface paramétrique bicubique construite sur 4x4 points de contrôle avec matrice de base B-Spline NRU selon les deux axes |
| Affichage en mode point |
|
|
|
Touches de curseur pour changer la position du point de contrôle sélectionné (en vert) Espace pour switcher entre les points de contrôle |
| Affichage en facettes avec un texturage |
|
|
|
Touches de curseur pour changer la position du point de contrôle sélectionné (en vert) Espace pour switcher entre les points de contrôle |
|
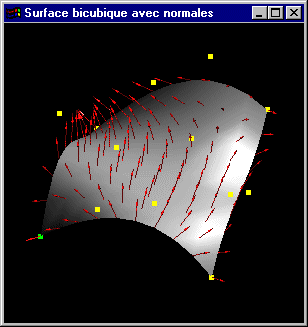
Affichage en facettes avec matérialisation des normales |
|
|
|
Enter pour switcher entre des affichages utilisant |
![]()
On appelle surface quadrique une surface d'équation :
f(x,y,z) = ax2 + by2 + cz2 + dxy + eyz + fxz + gx + hy + iz + j = 0.0
Cette famille de surfaces est très vaste.
Il est possible de représenter des plans, des sphères, des paraboloïdes, des ellipsoïdes, …
Les raisons qui pourraient faire utiliser les surfaces quadriques sont multiples :
- Calcul facile de la normale en un point à la surface
- Test facile de la présence d'un point sur la surface
- Calcul facile d'une des coordonnées si les deux autres sont connues
- Calcul possible de l'intersection d'une surface quadrique avec une autre surface quadrique
-
Plans: a = b = c = d = e = f = 0.0
-> f(x,y,z) = gx + hy + iz + j = 0.0 -
Ellipsoïdes: d = e = f = g = h = i = 0, j <= 0.0
-> f(x,y,z) = ax2 + by2 + cz2 + j = 0.0
Les surfaces et courbes lissées ont été initialement conçues comme outils de CFAO pour la modélisation d'objets.
Plus récemment, l'informatique graphique s'est emparée de ces objets mathématiques comme outils de modélisation pour représenter les objets des scènes qui ne seraient pas des objets canoniques "simples" (cube, sphère, ...) et qui seraient trop complexes à modéliser sous la forme d'un ensemble de facettes gérées individuellement. Les surfaces et courbes lissées viennent "s'intercaler" entre ces deux techniques de modélisation.
Les outils de haut niveau en modélisation pour la synthèse d'images font appel aux NURBS (Non Uniform Rational B-Splines) qui sont une évolution des B-Splines pour permettre un affichage en perspective.