L'illumination globale :
la radiosité
FACTEUR
DE FORME
Hémisphère
Hémicube
Introduction
Les algorithmes de rendu par Z-Buffer+Lambert+Gourond+Phong ou par ray-tracing sont assez approximatifs en terme d'évaluation des déplacements
d'énergie à l'intérieur des scènes.
Or, ce sont ces déplacements d'énergie qui ont pour conséquence l'éclairage et donc la coloration des objets.
Le principal problème non résolu est lié à la localité des éclairages : Un objet n'est éclairé que s'il n'est pas situé au delà d'un certain nombre de réflexions (réflexion diffuse, réflexion spéculaire ou réfraction) vis à vis de toutes les sources lumineuses définies "en tant que telles" dans la scène.
Tous les objets d'une scène sont de même nature, qu'il s'agisse de lumières ou bien d'objets graphiques classiques.
Ils émettent tous de l'énergie sous la forme de radiations électromagnétiques. Ce phénomène les rend colorés, donc visibles mais aussi lumineux
et donc à même d'éclairer les autres objets.
Ce spectre d'émission (la radiosité) est la somme de deux composantes (chacune pouvant éventuellement être nulle) :
- une énergie émise intrinsèquement,
- une énergie émise par réémission d'une partie des radiations reçues en provenance des autres objets présents dans la scène.
Ainsi, après une infinité (un très grand nombre) de réémissions successives des objets les uns sur les autres, un équilibre énergétique s’établit à l’intérieur de la scène.
Chaque objet de la scène est alors affecté d’une composante lumineuse colorée. C'est cette couleur que nous voyons.
-
Discrétisation de la scène en un ensemble de n surfaces.
-
Calcul, pour chaque couple de surfaces, de la fraction d’énergie qui, émise par la première, sera réceptionnée par la seconde (facteur de forme).
-
Constitution d’un système de n équations linéaires à n inconnues où les n inconnues sont les radiosités émises par chaque facette.
-
Résolution de ce système d’équations linéaires.
-
Affichage final par un algorithme classique d’élimination des parties cachées (Z-Buffer ou lancer de rayons).
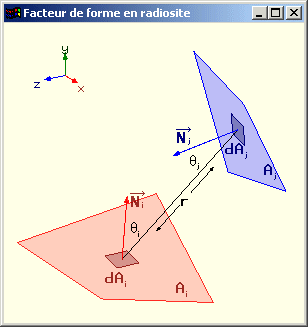
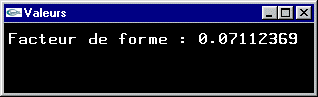
Calcul du facteur de forme entre deux surfaces
Le facteur de forme Fij est la fraction d’énergie qui quittant la facette i est reçue par la facette j.
Pour le calcul de Fij, on tient compte des forme et orientation respectives des deux facettes ainsi que de la présence éventuelle d’obstacles entre les deux.
|
Facteur de forme d'une surface vis à vis d'une surface |
|
|
|
Touches de curseur et/ou souris pour manipuler le schéma |
Le facteur de forme dFdidj d’une surface différentielle dAi vers une surface différentielle dAj est :
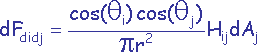
où qi est l’angle entre la normale à la surface Ai au point considéré et l’axe dAidAj, r est la longueur de cet axe et H est la valeur de la visibilité (0 ou 1) de dAj depuis dAi.
Cette définition différentielle doit être intégrée sur les deux surfaces Ai et Aj pour trouver la valeur recherchée.
C’est à dire :
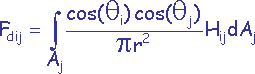
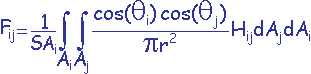
Problème : Réaliser cette intégration (qui est en fait une intégrale quadruple (surface-surface)).
Il n'existe pas de méthode analytique pour opérer cette intégration (même dans les cas les plus simples)
-> On emploie des solutions approximées.
Première approximation
On considère que Fij = Fdi j.
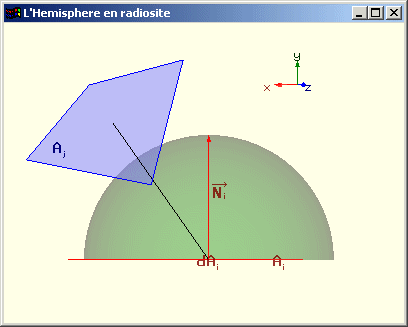
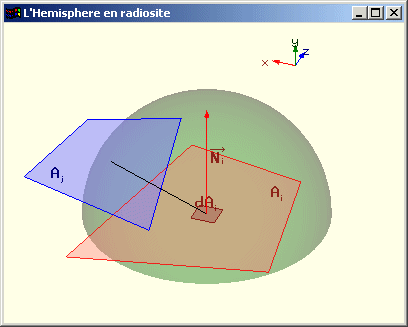
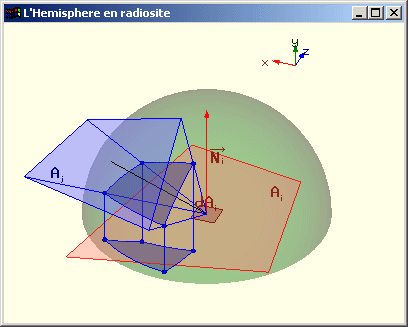
Calcul de Fdi j par projection sur l’hémisphère
Une estimation de Fdi j est effectuée en projetant toutes les portions de Aj visibles depuis dAi sur l'hémisphère de rayon unitaire centrée sur dAi et dont la base est parallèle à dAi.
On projette la portion de l'hémisphère ainsi définie sur le cercle base de l’hémisphère selon l’axe donné par la normale à Ai.
On divise l’aire de la surface obtenue par l’aire du cercle base.
|
Méthode de l'hémisphère pour le calcul des facteurs de forme |
|
|
|
Touches de curseur et/ou souris pour manipuler le schéma |
Cette méthode a pour inconvénient de requérir l’emploi d'un opérateur de projection sur une sphère. Cette opération est complexe et couteuse en temps. De plus, elle ne résoud pas le problème de la détermination des portions visibles.
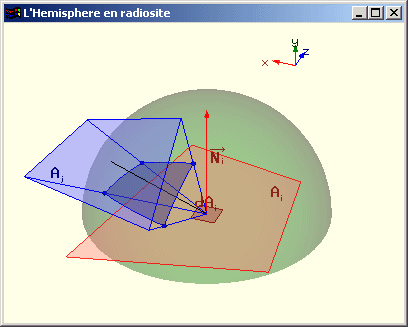
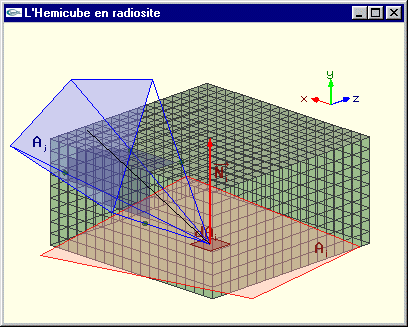
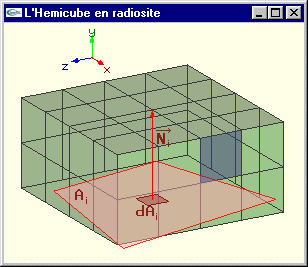
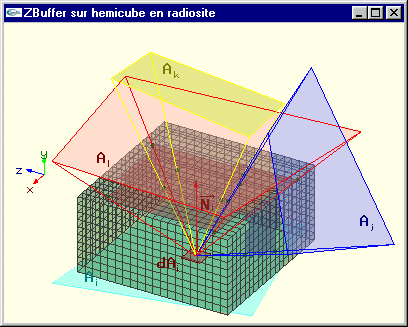
Calcul de Fdi j par projection sur l’hémicube
Principe : Projeter sur l’hémicube supérieur de centre dAi.
Chacune des cinq faces de l'hémicube est discrétisée en un certain nombre de cellules carrées identiques. On calcule quelles sont les cellules qui font partie de la surface projetée.
|
Méthode de l'hémicube pour le calcul des facteurs de forme |
|
|
|
+/- pour augmenter/diminuer la discrétisation de l'hémicube a, A, b, B, c et C pour déplacer la facette j Espace pour changer de facette j Touches de curseur et/ou souris pour manipuler le schéma |
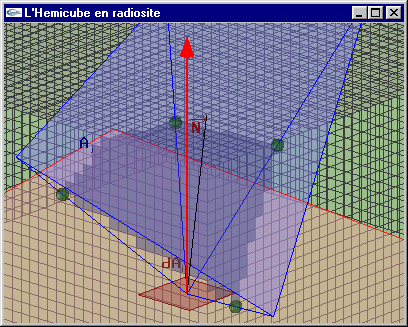
A chacune de ces cellules est associé un facteur de forme approximé
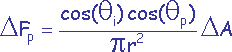
où qp est l’angle entre la normale à la cellule p et le vecteur entre dAi et p, r est la distance
entre dAi et p, et DA est la surface d’une cellule.
La somme des facteurs de forme élémentaires donne le facteur de forme total de la surface de départ.
On établit que pour une cellule p de coordonnées (xp,yp,zp) située sur l’hémicube :
-
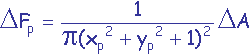 si p est une cellule située sur la face supérieure de l’hémicube.
si p est une cellule située sur la face supérieure de l’hémicube. -
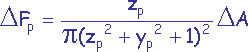 si p est une cellule située sur l’une des 2 faces perpendiculaires à l’axe x.
si p est une cellule située sur l’une des 2 faces perpendiculaires à l’axe x. -
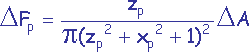 si p est une cellule située sur l’une des 2 faces perpendiculaires à l’axe y.
si p est une cellule située sur l’une des 2 faces perpendiculaires à l’axe y.
|
Méthode de l'hémicube pour le calcul des facteurs de forme Valeurs des facteurs de forme élémentaires des cellules de l'hémicube |
|
|
|
+/- pour augmenter/diminuer la discrétisation de l'hémicube a, A, b et B pour déplacer la cellule testée Espace pour changer de face sur l'hémicube Touches de curseur et/ou souris pour manipuler le schéma |
Plus la discrétisation de l’hémicube est poussée, meilleure est l’estimation du facteur de forme, mais plus long est le calcul.
La technique précédente permet de calculer une bonne approximation du facteur de forme d'une facette vis à vis d'une autre facette.
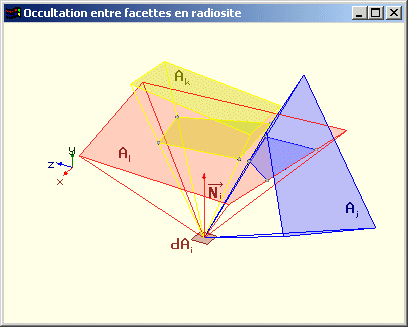
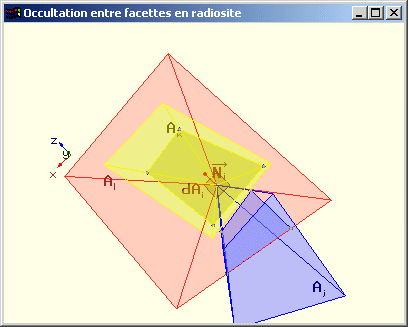
Problème : Elle ne permet pas de tenir compte des occultations éventuelles entre les facettes.
|
Occultations entre facettes pour le calcul des facteurs de forme |
|
|
|
Touches de curseur et/ou souris pour manipuler le schéma |
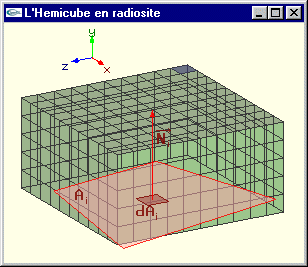
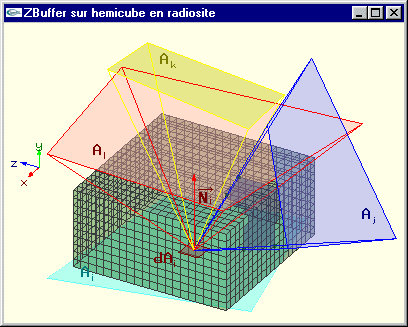
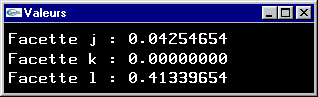
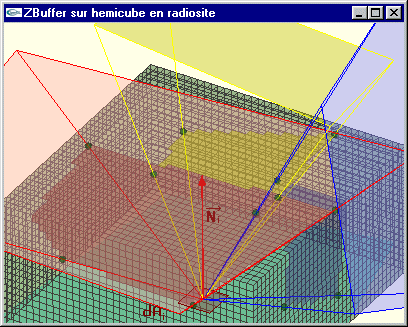
Pour résoudre ce problème, on réalise un Z-Buffer de la scène sur chacun des cinq plans de projection.
Cette technique réalise l'élimination des parties cachées depuis dAi pour l'ensemble des surfaces de la scène en projection sur chacune des cinq faces de l'hémicube.
|
Calcul d'une ligne de facteurs de forme en tenant compte des occultations |
|
|
|
Enter pour switcher entre une des trois facettes et les trois facettes ensemble pour le calcul des facteurs de forme a, A, b, B, c et C pour déplacer une facette Espace pour changer la facette déplaçable +/- pour augmenter/diminuer la discrétisation de l'hémicube Touches de curseur et/ou souris pour manipuler le schéma |
En fait, on calcule la matrice de facteurs de forme non plus composante après composante, mais ligne après ligne.
La technique de calcul des facteurs de forme par hémicube s'est imposée au cours du temps car elle permet de s'appuyer sur l'implantation hard du Z-Buffer réalisée sur les adaptateurs graphiques et est donc ainsi "rapide".
Constitution du système d’équations linéaires
Soit une surface i.
On établit
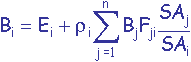
où Bi et Bj sont les radiosités des surfaces i et j (mesurées en énergie/unité de temps/unité de surface), Ei est l’énergie intrinsèque émise par la surface i, ri est la réflectivité de la surface i, Fji est le facteur de forme de la surface j vers la surface i et Ai et Aj sont les aires des surfaces i et j.
On établit aussi que Ai Fij = Aj Fji
->
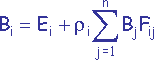
On obtient le système d’équations linéaires :
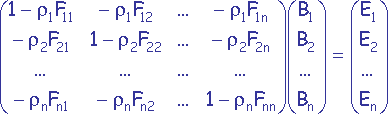
Remarque : La diagonale n’est pas forcément égale à 1 (le facteur de forme d'une surface vis à vis d'elle-même peut être différent de 0) car une surface s non plane peut s’éclairer elle-même.
Résolution du système d’équations linéaires
On résout généralement le système d'équations par une méthode itérative : Gauss-Seidel ou Jacobi par exemple.
-> On arrête la résolution du système à l'itération permettant d'atteindre le niveau de précision désiré (invariance entre deux états successifs obtenue sur les radiosités ou les images affichées avec ces radiosités).
Ce système d’équations est résolu pour les trois composantes rouge, verte et bleue (valeurs de réflectivité et d'émission intrinséque différentes dans le système d'équations linéaires) permettant ainsi d’obtenir des images colorées.

Radiosité avec affichage par Z-Buffer et ombrage plat

Radiosité avec affichage par Z-Buffer et ombrage de Gouraud

Mise en évidence de réflexions colorées

Mise en évidence de réflexions colorées
-
Au niveau de la qualité de l’affichage
On obtient une très bonne estimation des flux d'énergie à l'intérieur de la scène.
-> Des images très réalistes du point de vue des éclairages sont créées.
Le calcul de l’équilibre énergétique intègre de manière très précise le calcul de la composante de lumière ambiante de chaque surface, ce qui conduit généralement à des lumières douces qui semblent tamisées (résolution des problèmes d'illumination locale inhérents aux autres algorithmes de rendu). Les scènes d'intérieur tire un grand profit de ce type de rendu.
La réalisation de l'algorithme d'affichage (par exemple un Z-Buffer associé à un lissage de Gouraud) renforce encore ce phénomène.
On modélise les ombres portées car on gère les occultations entre objets.
-
Au niveau de la rapidité de calcul
Une fois l’équilibre énergétique calculé, l’affichage d’une scène est très rapide (rapidité du Z-Buffer ou du lancer de rayons).
Contrairement au lancer de rayons, on n’a pas à recalculer l’équilibre si on effectue un déplacement de l'observateur à l’intérieur de la scène. Tant que la scène n’est pas modifiée, les calculs d’animation sont extrêmement rapides.
-
Au niveau de la qualité de l’affichage
Cet algorithme ne tient compte que de la lumière "diffusée". Il ne peut pas rendre compte des transmissions et des réflexions spéculaires.
La discrétisation de la scène et des calculs de facteurs de forme par méthode de l'hémisphère ou l'hémicube fait que certains problèmes d'aliasage peuvent apparaître entraînant des problèmes comme par exemple sur les ombres :
- bords trop flous et/ou crénelés,
- ombres portées absentes pour les objets trop minces,
ou sur les éclairages :
- mauvais éclairage de certaines zones (apparition de motifs en "taches de léopard"),
- manque de précision sur l'éclairage des objets placés près de l'observateur et donc apparaissant gros à l'écran.
-
Au niveau de la rapidité de calcul
Les deux phases (a) de calcul des facteurs de forme et (b) de résolution du système d’équations linéaires demandent des quantités de calcul importantes. La phase de calcul des facteurs de forme est la plus longue.
Plus on veut un résultat proche de la réalité, plus la discrétisation de la scène doit être poussée et donc plus le temps de calcul est important. De plus, on est confronté à la résolution successive de deux problèmes en n2 du nombre de facettes (potentiellement très grand) :
- le calcul et le stockage des facteurs de forme,
- la résolution du système.
Radiosité progressive
Le problème de la structure de données en n2 trouve sa solution avec la technique de radiosité progressive.
Cette technique a pour but de résoudre progressivement le système d'équations linéaires sans stockage de l'ensemble de la matrice des facteurs de forme. On ne la calcule que ligne par ligne au moment où chaque ligne est utilisée lors de la résolution du système d'équations linéaires.
L'algorithme est itératif, basé sur une boucle infinie. Il traite les surfaces de la scène les unes après les autres pour évaluer et affecter l'énergie
qu'elles émettent vers les autres surfaces.
Une énergie déjà émise n'a plus à être émise.
-> On utilise deux tableaux pour stocker les radiosités déjà calculées, mais aussi les portions de ces radiosités qui n'ont pas encore été émises
(créées, depuis la dernière émission, par réception depuis les autres facettes puis réémission).
Algorithme
Déclarer un tableau d'énergie B destiné à contenir la radiosité
de chacune des n surfaces
Déclarer un tableau d'énergie DB destiné à contenir l'énergie restant à émettre par chacune des n surfaces (énergie reçue depuis la dernière
émission)
Initialiser B et DB avec les valeurs d'énergie émise intrinsèquement par chaque surface
Faire
Choisir une surface F parmis les n surfaces (par exemple celle présentant la valeur DB maximale)
Calculer le tableau de facteurs de forme FF associé à F
// Allouer la fraction d'énergie émise par F à chacune des autres facettes
pour chaque surface FA
// Calculer l'énergie reçue par FA de la facette F et réémise
DR = roFA * DB[F] * FF[FA] * AF / AFA
// Incrémenter les tableaux DB et B avec l'énergie réémise par FA
DB[FA] += DR
B[FA] += DR
fin pour
// Mettre à 0 l'énergie restant à émettre par la surface f
DB[F] = 0
Calculer l'image correspondant aux n surfaces affectées des radiosités stockées dans B
Tant que l'image n'est pas satisfaisante
On sait que cette technique de résolution permet la convergence vers la bonne solution. Un problème est que le temps de convergence ne peut pas être contrôlé.
Le seul contrôle offert par cet algorithme concerne le choix de la surface F considérée à chaque itération. On accélère la convergence en choisissant la surface possédant la radiosité maximale restant à émettre.
Remarque : On peut être appelé à calculer plusieurs fois, au cours de l'exécution, la ligne de facteurs de forme concernant une surface.


Radiosité progressive
Convergence vers l'image définitive
On limite les problèmes d'aliasage en utilisant une technique de discrétisation de la scène permettant d'augmenter la précision (augmenter le nombre de surfaces) dans les zones critiques.
La technique généralement employée consiste à subdiviser récursivement les surfaces.
On pourra détecter ces zones critiques par le fait que deux surfaces voisines situées à leurs limites présentent des valeurs Fdi-j différant d'une valeur supérieure à une limite prédéfinie.

Une cathédrale

Une usine
La technique de calcul de l'illumination globale permet de calculer au mieux la composante de lumière ambiante due aux réflexions diffuses multiples (infinies) générées sur chaque surface diffusante d'une scène. Elle permet l'obtention d'images de très bonne qualité aux lumières douces telles qu'elles apparaissent très souvent dans la réalité quand les éclairages sont indirects ou diffus.
Cet effet est renforcé par la définition possible, contrairement au lancer de rayons, de sources lumineuses non ponctuelles (surfaces lumineuses) et par la réalisation de l'algorithme d'affichage.
L'obtention d'images photoréalistes se heurte à l'impossibilité de modéliser les réflexions spéculaires et les transmissions.
Une technique fréquement employée pour obtenir des images de grande qualité consiste à faire précéder un rendu par lancer de rayons, d'une phase de calcul des radiosités permettant une évaluation correcte des éclairages ambiants.
Un autre inconvénient des calculs de radiosité est la lenteur.