Sujets et Corrections
de TD et TP
TD n°1
Création de scènes
en VRML 1.0
TP n°1
Prise en mains
d'un environnement
de programmation
VRML
TD n°2
Création de scènes
OpenGL
TP n°2
Prise en mains
d'un environnement
de programmation
OpenGL
TD n°3
Utilisation
des primitives
graphiques
en OpenGL
TP n°3
Interactivité
clavier et souris
avec GLUT
et OpenGL
TD n°4
Animation
avec GLUT
et OpenGL
TP n°4
Gestion des caméras
en OpenGL
TD n°5
Gestion des caméras
en VRML
TP n°5
Matériaux
et lumières
en VRML
TD n°6
Calcul
de la diffusion
au moyen
de la formule
de Lambert
TP n°6
Matériaux
et lumières
en OpenGL
TD n°7
Mathématiques
pour l'infographie
TP n°7
Mathématiques
des matrices
TD n°8
Manipulation
des bitmaps
et placage
de texture
en OpenGL
TP n°8
Mathématiques
des matrices
TD n°9
Placage
de texture
en OpenGL
TD n°10
Découpage
par l'algorithme
de Cohen-Sutherland
Dernière modification
16/11/09 07:03:36
TD n°1: Création de scènes VRML 1.0
Exercice n°1
(1) Programmer en VRML la scène suivante sans utiliser le nœud Separator ailleurs que pour le Separator d'encadrement global du fichier:
Quatre cubes de coté de longueur 1.0 aux positions (2.0,0.0,2.0), (2.0,0.0,-2.0), (-2.0,0.0,2.0) et (-2.0,0.0,-2.0).
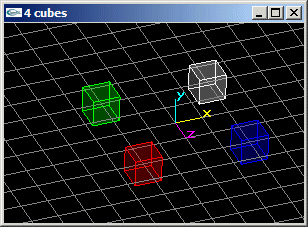
(2) Reprogrammer en VRML la scène de la question (1) en utilisant le nœud Separator pour rendre les objets indépendants les uns des autres.
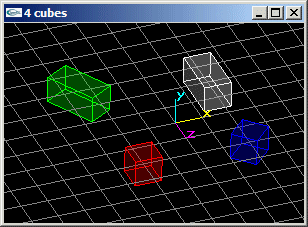
(3) Reprogrammer en VRML la scène en apportant les modifications suivantes:
- Le cube en position (2.0,0.0,2.0) subit une rotation de 45° autour de l'axe y passant par son centre.
- Le cube en position (2.0,0.0,-2.0) subit un zoom de rapport (1.0,1.0,2.0) par rapport à son centre.
Le cube en position (-2.0,0.0,-2.0) n'est plus centré en ce point. Il est placé de telle manière qu'il présente une rotation de 30° autour de l'axe y passant par le sommet (-2.0,0.0,-2.0) et que ce sommet soit le centre de sa base inférieure. En outre, il subit un zoom de rapport (1.0,1.0,2.0) par rapport à son centre.
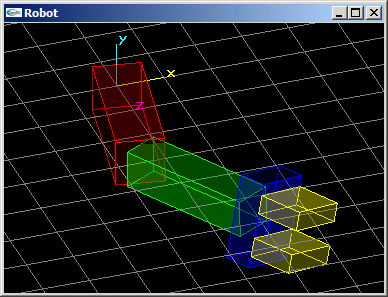
Exercice n°2
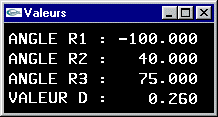
Programmer la scène modélisant un bras robot composé d'un avant-bras,
d'un bras, et d'une paire de pinces.
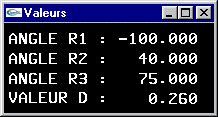
L'avant-bras est articulé pour tourner autour de l'axe y d'un angle r1. Il s'agit d'un
parallélépipède rectangle de dimension (3.0,1.0,1.0) (rouge). Le bras est articulé
autour de l'axe y au bout de l'avant bras pour un angle r2. Il s'agit d'un
parallélépipède rectangle de dimension (3.0,0.8,0.8) (vert). La pince est située au
bout du bras. Elle peut tourner autour de l'axe du bras pour un angle r3. L'embase de la
paire de pinces est un parallélépipède rectangle de dimension (0.6,1.2,1.8) (bleu).
Chacune des mâchoires est un parallélépipède rectangle de dimension (1.0,1.2,0.4)
(jaune) à même de se déplacer longitudinalement d'une valeur d pour réaliser une
ouverture totale de 2xd.
![]()
TP n°1: Prise en mains d'un environnement de programmation VRML
Les viewers disponibles sont:
- Un plugin Internet Explorer/Netscape Navigator (Cortona Player)
- Une application de visualisation (Scene Viewer)
Travail demandé:
- Implantation des 2 fichiers VRML du TD n°1.
- Implantation d'une scène avec un cube, une sphère, un cylindre et un cone pour vérifier le centrage et l'axe de dessin de ces objets.
- Modification du bras robot pour que l'avant bras et le bras soient transformés en cylindres de diamètre 1.0 et 0.8 et de hauteur 3.0 et que l'articulation soit modélisée par un objet supplémentaire de type sphère de diamètre 1.4.

- Nouvelle modification du bras robot pour que les mandibules soient transformées en des cônes de rayon 0.2 et de hauteur 2.0 pointant vers l'intérieur de la pince avec un angle de r4 radians par rotation autour du centre de leurs bases.
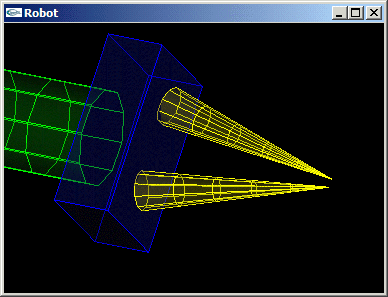
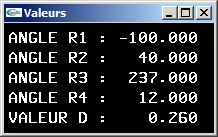
| Scène (2) |
| Scène (3) |
| Le bras robot |
| Test des objets |
| Le bras robot avec cylindres |
| Le bras robot avec cylindres et cones |
![]()
TD n°2: Création de scènes OpenGL
Exercice n°1
Soit la scène composée de n parallélépipèdes rectangles de dimension (5.4, 0.3, 1.0) centrés sur les sommets d'un polygone régulier de rayon 3 lui-même centré sur O et plongé dans le plan xOy. Ces objets doivent présenter leur face de dimension (0.3, 1.0) directement orientée vers O tel que le montre la copie d'écran ci-dessous.
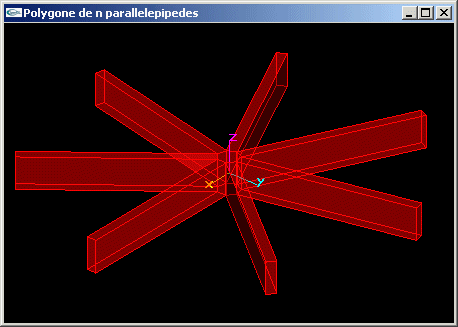
Réaliser l'implantation OpenGL de cette scène en tant que fonction C.
Exercice n°2
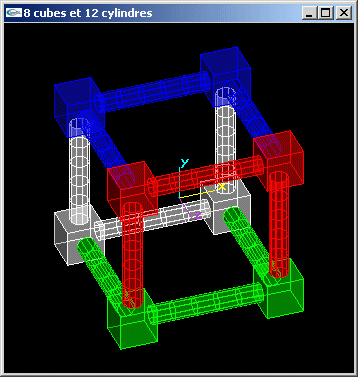
Soit la scène composée de huit cubes de cotés 1 centrés sur les
sommets d'un cube de rayon 4 lui-même centré sur O, et de 12 cylindres de rayon 0.25 et
de longueur 3.0 joignant ces 8 sommets entre eux pour matérialiser les arêtes du cube de
coté 4.
Implanter cette scène en une fonction C.
Fichiers sources pour dessiner des cylindres
ModuleCylindres.cpp
ModuleCylindres.h
![]()
TP n°2: Prise en mains d'un environnement de programmation OpenGL
Création d'un projet Visual C++ permettant la compilation OpenGL
- Les fichiers d'inclusion (nécessaires à la compilation) spécifiques à OpenGL sont GL/gl.h et GL/glu.h ainsi que GL/glut.h si GLUT est utilisé.
- Les librairies d'édition de liens (nécessaires à la création de l'exécutable) spécifiques à OpenGL sont OpenGL32.lib et glu32.lib ainsi que glut32.lib si GLUT est utilisé.
- Les dll (nécessaires à l'exécution) spécifiques à OpenGL sont OpenGL32.dll et glu32.dll ainsi que glut32.dll si GLUT est utilisé.
Téléchargement du programme source exemple destiné à être compilé et testé: Simple2006-2007.cpp.
Téléchargement du programme source exemple fonctionnel (définition d'une caméra, gestion du clavier, gestion correcte du fenêtrage, dessin d'une scène élairée ou non) destiné à être compilé et testé: OpenGL2006-2007.cpp.
Téléchargement du programme source exemple (animation) destiné à être testé: Animation2006-2007.cpp.
Dessin des objets de base GLUT pour repérer leurs caractéristiques de taille, d'orientation et de facettisation (en adaptant l'exemple OpenGL2006-2007.cpp).
Implantation des exercices du TD n°2 (en adaptant l'exemple OpenGL2006-2007.cpp).
Fichiers sources pour dessiner des cylindres
ModuleCylindres.cpp
ModuleCylindres.h
![]()
TD n°3: Les primitives graphiques en OpenGL
Exercice n°1
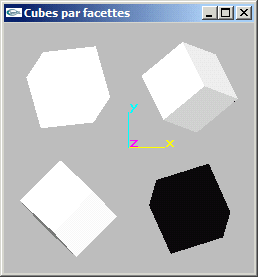
a) Ecrire une fonction de modélisation d'une boite cubique de dimension c centrée sur l'origine du repère. Cette fonction devra seulement assurer la création des facettes (cubes blanc et noir uniforme sur l'image proposée).
b) Modifier la fonction précédente pour y inclure la gestion des normales aux facettes (utilisées par OpenGL pour les calculs d'éclairage) (cubes gris ombrés sur l'image proposée).
Exercice n°2
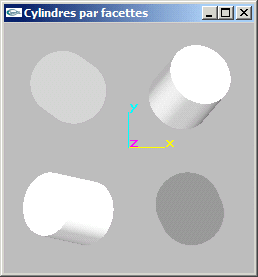
a) Ecrire une fonction de modélisation d'un cylindre de rayon r, de hauteur h, possédant n sections radiales, centré sur l'origine et d'axe y. Cette fonction devra seulement assurer la création des facettes (cylindres gris uniformes sur l'image proposée).
b) Modifier la fonction précédente pour y inclure la gestion des normales aux facettes (utilisées par OpenGL pour les calculs d'éclairage) (cylindres avec ombrage gris sur l'image proposée).
![]()
TP n°3: Intéractivité clavier et souris avec GLUT et OpenGL
Exercice n°1
On considère un programme affichant un objet quelconque au choix.
- Implanter un contrôle clavier permettant de changer la taille d'affichage de cet objet au moyen des touches + et -.
- Implanter les contrôles clavier permettant de faire tourner cet objet sur lui-même par utilisation des touches up, down, left, right et éventuellement page up et page down.
- Implanter les contrôles clavier permettant déplacer cet objet dans la fenêtre d'affichage au moyen des touches x, X, y, Y, z et Z.
Exercice n°2
On considère un programme affichant un objet quelconque au choix.
Implanter un contrôle souris permettant de faire tourner cet objet sur lui-même.
![]()
TD n°4: Programmation d'animations avec GLUT et OpenGL
Exercice n°1
On considère une scène quelconque modélisée par une fonction void
scene(void).
Ecrire les fonctions display et idle d'un programme C+GLUT+OpenGL permettant d'afficher et
d'animer cette scène par rotation autour de l'axe Ox.
Exercice n°2
On considère une scène composée d'une sphère se déplacant cycliquement sur une trajectoire carrée (dans le plan xOy, centré sur O, longueur du coté = c) par pas d'incrément delta entre deux images.
Ecrire les fonctions display et idle d'un programme C+GLUT+OpenGL permettant d'afficher cette animation.
Implanter un contrôle clavier permettant d'utiliser la touche ESPACE pour activer/désactiver l'animation.
![]()
TP n°4: Gestion des caméras en OpenGL
Exercice n°1
On considère une scène quelconque occupant un volume sphérique de rayon 4.5.
Cette scène est affichée au moyen d'une caméra de visualisation en projection parallèle orthographique orientée selon l'axe -z.
a) Quelle ouverture définiriez-vous pour visualiser cette scène si celle-ci est centrée sur l'origine du repère de modélisation?
b) Quelle ouverture définiriez-vous pour visualiser cette scène si celle-ci est centrée sur le point de coordonées (10.0, 10.0, 10.0) du repère de modélisation?Cette scène est affichée au moyen d'une caméra de visualisation en perspective orientée selon l'axe -z et placée en position (0.0, 0.0, 0.0).
a) Quelle ouverture définiriez-vous pour visualiser cette scène si celle-ci est centrée sur le point de coordonées (0.0, 0.0, -10.0) du repère de modélisation?
b) Quelle ouverture définiriez-vous pour visualiser cette scène si celle-ci est centrée sur le point de coordonées (0.0, 0.0, -100.0) du repère de modélisation?
Exercice n°2
On considère une scène quelconque occupant un volume sphérique de rayon 4.5.
Cette scène est affichée au moyen d'une caméra de visualisation en projection parallèle orthographique orientée selon l'axe -z.
a) A quelles positions en z placeriez-vous les plans de découpage near et far pour visualiser cette scène si celle-ci est centrée sur l'origine du repère de modélisation?
b) A quelles positions en z placeriez-vous les plans de découpage near et far pour visualiser cette scène si celle-ci est centrée sur le point de coordonées (10.0, 10.0, 10.0) du repère de modélisation?Cette scène est affichée au moyen d'une caméra de visualisation en perspective orientée selon l'axe -z et placée en position (0.0, 0.0, 0.0).
A quelles positions en z placeriez-vous les plans de découpage near et far pour visualiser cette scène si celle-ci est centrée sur le point de coordonées (0.0, 0.0, -10.0) du repère de modélisation?Cette scène est affichée au moyen d'une caméra de visualisation en perspective placée en position (-10.0, -5.0, 10.0) et orientée vers le centre de la scène.
A quelles positions en z placeriez-vous les plans de découpage near et far pour visualiser cette scène si celle-ci est centrée sur le point de coordonées (0.0, 0.0, -10.0) du repère de modélisation?
Exercice n°3
Vérifier les résultats des exercices n°1 et n°2 via une implantation. On utilisera les fonctions glOrtho, gluPerspective et gluLookAt au sein de la fonction "reshape" et on adaptera la fonction display en fonction des conditions particulières de placement de la scène.
GLUt |
||
| Gestion de caméras | ||
![]()
TD n°5: Gestion des caméras en VRML
Exercice n°1
On considère une scène quelconque centrée sur l'origine du repère.
On souhaite visualiser cette scène de telle manière que son centre soit affiché au
centre de la fenêtre d'affichage.
Notre caméra de visualisation "regarde" par défaut selon l'axe -z. Une seule
rotation est autorisée pour l'orienter selon la direction souhaitée. Cette rotation peut
être définie selon n'importe quel axe (i.e. pas forcément uniquement (1, 0, 0), (0, 1,
0) ou (0, 0, 1), mais aussi tout axe (dx, dy, dz) tel que dx, dy et dz non nuls
simultanément) et n'importe quel angle
Définir la rotation à réaliser pour chacun des 4 points de vue
(position de la caméra) suivants:
(a) (0.0, 0.0, 100.0),
(b) (0.0, 0.0, -100.0),
(c) (100.0, 0.0, 100.0),
(d) (100.0, 100.0, 100.0).
Exercice n°2
On souhaite implanter les 4 points de vue de l'exercice n°1 dans le cadre
de 4 fichiers VRML.
La caméra choisie est la caméra de visualisation en perspective. La scène possède un
rayon voisin de 5. On souhaite la visualiser en "gros plan".
Définir les noeuds caméra que vous utiliseriez.
![]()
TP n°5: Matériaux et lumières en VRML
Dans les exercices suivants, on s'attachera à tester les diverses options de rendu relatives à la gestion des ombrages proposée par le viewer VRML utilisé.
Exercice 1
a) Ecrire une scène VRML composée d'une sphère de rayon 5 centrée sur l'origine du repère et affectée d'un matériel avec uniquement de la diffusion dans le rouge. Tester l'activation/désactivation de la lampe frontale.
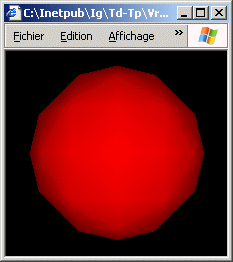
b) Modifier la scène précédente pour que le matériel intègre une réflexion spéculaire dans le vert.
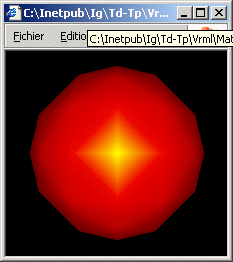
c) Modifier la scène précédente pour y intégrer un éclairage sous la forme d'une source lumineuse directionnelle blanche éclairant depuis la droite. Désactiver la lampe frontale.

d) Modifier la scène précédente pour y inclure une seconde sphère de rayon 2 placée en position (10, 0, 0) possédant le même matériel que la première ainsi qu'une seconde source lumineuse ponctuelle blanche placée à l'origine.
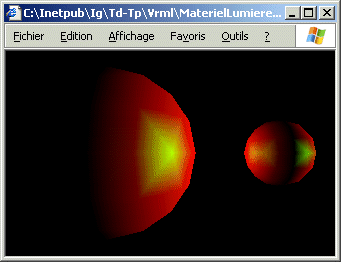
e) Modifier la scène précédente pour y inclure une source lumineuse
spot placée en position (0, 0, 10) orientée vers l'origine et éclairant partiellement
la grosse sphère.
Tester les différentes préférences de votre viewer VRML.

Solutions
VRML |
||||||
| Les fichiers VRML | ||||||
Exercice 2
Reprendre l'exercice précédent avec le matériel suivant:
Material {diffuseColor 0 1 0
specularColor 0 0 1
shininess 0.25
ambientColor 1 0 0
emissiveColor 0.2 0.2 0.2
transparency 0
}
Analyser les contributions respectives des différentes caractéristiques de ce matériel.
Solution
VRML |
||||||
| Les fichiers VRML | ||||||
![]()
TD n°6: Calcul de la diffusion au moyen de la formule de Lambert
Le travail est à réaliser en langage java.
Exercice n°1
a) Définir une classe position dans un espace à 3 dimensions
b) Définir une classe direction dans un espace à 3 dimensions
c) Définir une classe couleur RVB.
d) Définir une classe destinée à modéliser un matériel générant des réflexions diffuses.
e) Définir une classe destinée à modéliser une lumière directionnelle
f) Définir une classe énergie RVB.
g) Implanter une méthode de calcul de l'énergie colorée diffusée au niveau d'un point d'une surface munie d'un matériel sous l'éclairage d'une lumière directionnelle. La normale au point vis à vis de la surface est connue.
Exercice n°2
a) Définir une classe destinée à modéliser une lumière ponctuelle
b) Implanter une méthode de calcul de l'énergie colorée diffusée au niveau d'un point d'une surface munie d'un matériel sous l'éclairage d'une lumière ponctuelle. La normale au point vis à vis de la surface est connue.
![]()
TP n°6: Matériaux et lumières en OpenGL
Exercice n°1
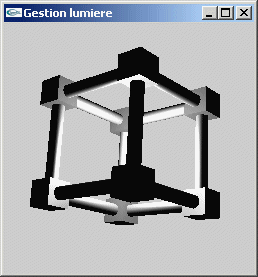
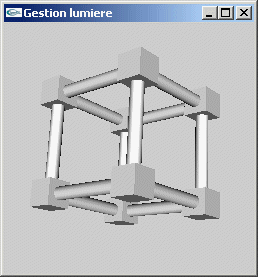
On considère la scène composée du cube schématisé par des cylindres et des cubes
au cours du TD n°2.
Programmer un éclairage pour cette scène contrôlé via le clavier permettant de choisir
entre une source ponctuelle blanche placée à l'origine et une source directionnelle
blanche éclairant selon la direction (0.0,0.0,1.0).
Le matériel de l'objet est diffusant dans le blanc et réfléchissant spéculairement
dans le rouge.
Implanter des contrôles clavier supplémentaires permettant de modifier chacune des deux
lumières pour en gérer les composantes diffuse et spéculaire (couleur, intensité,
...).
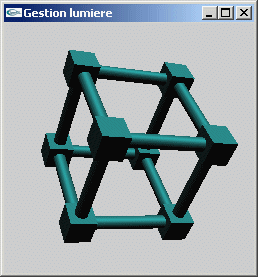
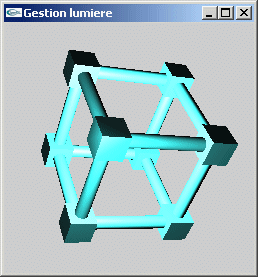
Exercice n°2
On considère deux sources lumineuses ponctuelles placées en position (3.0, 0.0, z) et
(-3.0, 0.0, z) avec z = 1.0. La première est verte. La seconde est rouge.
La scène affichée est composée d'une surface plane blanche située dans le plan xOy.
a) Implanter un mouvement d'animation tel que les sources lumineuses réalisent un déplacement circulaire autour du point de coordonnées (0.0, 0.0, z).
b) Implanter des contrôles clavier permettant de faire varier z et de faire tourner l'ensemble de la scène (objet + lumières) autour de l'axe x.
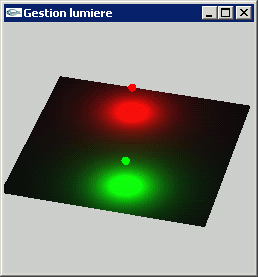
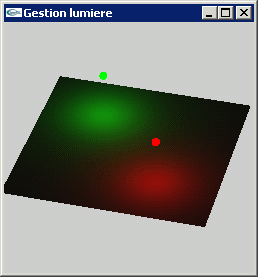

![]()
TD n°7: Mathématiques pour l'infographie
Le travail est à réaliser en langage java en utilisant comme base les classes du TD n°6.
Exercice n°1
a) Développer une méthode de calcul de la distance entre deux positions
b) Développer une méthode de calcul de la norme d'une direction
c) Développer une méthode de normalisation d'une direction
d) Développer un constructeur de la classe direction pour calculer la direction normée entre deux positions.
e) Développer une méthode de calcul du produit scalaire de deux directions
f) Développer une méthode de calcul du produit vectoriel de deux directions
Exercice n°2
a) Définir une classe permettant de représenter géométriquement un rayon lumineux émis depuis une position arbitraire dans une direction arbitraire
b) Définir une classe permettant de représenter géométriquement une sphère arbitraire.
c) Développer une méthode permettant de tester si un rayon lumineux intercepte une sphère.
d) Développer une méthode permettant de calculer la position la plus proche du point d'émission d'un rayon lumineux parmi toutes les positions des intersections entre ce rayon lumineux et une sphère (s'il en existe au moins une).
![]()
TP n°7: Mathématiques des matrices
Le TP est à réaliser en java.
a) Développer les bases d'une classe vecteur de Rn (n "lignes").
b) Développer les bases d'une classe matrice de Rmp (m lignes, p colonnes).
c) Développer deux méthodes java permettant de réaliser les produits matrice.vecteur et matrice.matrice.
e) Développer une classe vecteur spécifique pour la dimension 4.
f) Développer une classe matrice spécifique pour la dimension 4x4.
g) Test des classes des questions e) et f) sur les matrices et vecteurs suivants:
M1 = 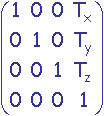 , M2 =
, M2 = 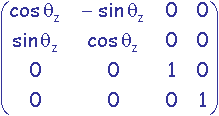
V1 = ![]() , V2 =
, V2 = ![]()
avec application numérique sur les valeurs Tx, Ty, Tz, Qz, x, y et z.
On réalisera et analysera les résultats des produits M1.V1, M1.V2, M2.V1, M2.V2, M1.(M2.V1), (M1.M2).V1, M2.(M1.V1) et (M2.M1).V1.
![]()
TD n°8: Manipulation des bitmaps et placage de texture en OpenGL
Les principales fonctions OpenGL utilisées dans le cadre du texturage sont:
- glEnable(GL_TEXTURE_2D) pour activer le texturage 2 dimensions,
- glPixelStorei(GL_UNPACK_ALIGNMENT,1) pour permettre à OpenGL de travailler sur des bitmaps avec une précision de 1 pixel,
- glTexParameterf(GL_TEXTURE_2D,GL_TEXTURE_MAG_FILTER,GL_NEAREST)
et
glTexParameterf(GL_TEXTURE_2D,GL_TEXTURE_MIN_FILTER,GL_NEAREST)
pour spécifier la technique de placage de texture, - glTexImage2D(...) pour spécifier l'image à plaquer,
- glTexCoord2f(x,y) pour spécifier la prochaine coordonnée de texturage à utiliser pour un sommet créé via la fonction glVertex[] dans une primitive graphique.
![]()
TP n°8: Mathématiques des matrices
Le TP est à réaliser en java. Il s'incrit comme la suite du TP n°7.
a) Développer une classe "vecteur" spécifique pour la représentation de positions dans un espace à trois dimensions.
b) Développer une classe "vecteur" spécifique pour la représentation de directions dans un espace à trois dimensions.
c) Développer une classe "matrice" spécifique pour la représentation de translations dans un espace à trois dimensions.
d) Développer trois classes "matrice" spécifiques pour la représentation de rotations autour des axes Ox, Oy et Oz dans un espace à trois dimensions.
e) Développer une classe "matrice" spécifique pour la représentation de rotations autour d'un axe arbitraire normé ou non dans un espace à trois dimensions.
f) Tester expérimentalement l'associativité du produit matrice x matrice.
g) Prouver expérimentalement la non commutatitivité du produit matrice x matrice.
h) Développer une classe "matrice" spécifique pour la représentation de la
transformation géométrique de type "passage de coordonnées globales en
coordonnées observateur" où la position de l'observateur Po et la position d'un
point visé Pv sont connues et où les "verticales" (l'axe y) sont conservées (voir ce lien).
Application numérique:
On donne Po = (25.0, 12.0, 5.0), Pv = (-10.0, 2.0, -6.0)
Quelle est la position du point transformé du point Po?
Quelle est la position du point transformé du point Pv?
Quelle est la position du point transformé de l'origine?
Quelle est la direction transformée de la direction normée Po vers Pv?
Quelle est la direction transformée de la direction (1.0, 0.0, 0.0)?
Quelle est la direction transformée de la direction (0.0, 1.0, 0.0)?
Quelle est la direction transformée de la direction (0.0, 0.0, 1.0)?
![]()
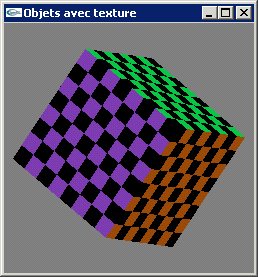
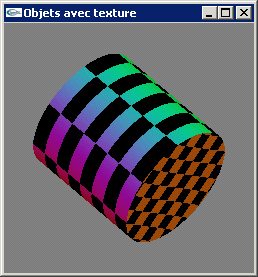
TD n°9: Placage de texture en OpenGL
a) Ecrire une fonction C d'allocation et d'initialisation d'un tableau d'octets non signés matérialisant une bitmap RVB dessinant un damier de 8x8 pixels noir et blanc.
b) Reprendre la fonction de dessin de cube du TD n°3 pour y intégrer la génération des coordonnées de texturage utilisé lors d'un placage de texture 2D.
c) Reprendre la fonction de dessin de cylindre du TD n°3 pour y intégrer la génération des coordonnées de texturage utilisé lors d'un placage de texture 2D.
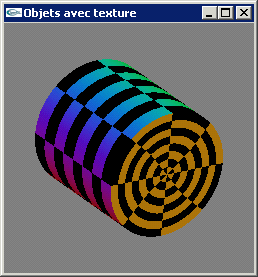
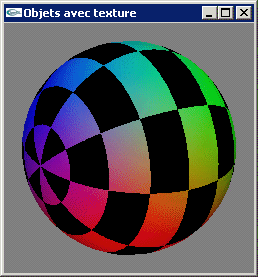
d) On considère l'équation paramètrique d'une surface sphérique suivante:
| a appartient à [-p/2,p/2] b appartient à [0,2p] |
 |
Définir une technique de calcul des coordonnées de texturage utilisable lors d'un placage de texture 2D sur une telle surface.
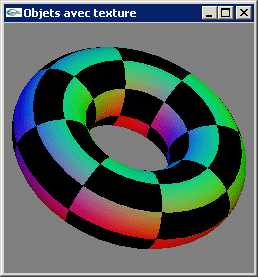
d) On considère l'équation paramètrique d'une surface torique suivante:
| a appartient à [0,2p] b appartient à [0,2p] |
 |
Définir une technique de calcul des coordonnées de texturage utilisable lors d'un placage de texture 2D sur une telle surface.
GLUt |
||
| Texturage d'objets | ||
![]()
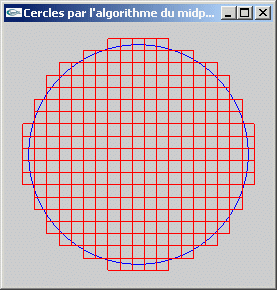
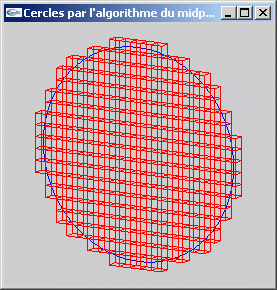
TP n°9: Remplissage de cercles
a) Implanter l'algorithme du midpoint pour le tracé de cercles.
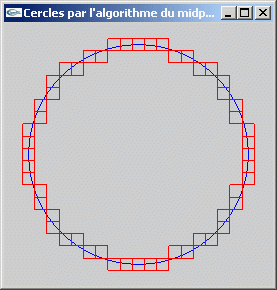
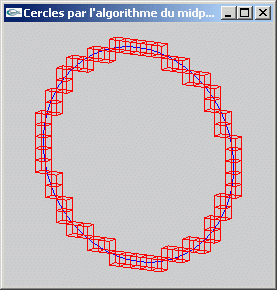
b) A partir de l'implantation de la question (a), développer une fonction de remplissage de cercles.
![]()
TD n°10: Découpage par l'algorithme de Cohen-Sutherland
L'implantation est réalisée en langage java.
a) Définir trois classes de stockage pour:
- des positions en deux dimensions,
- des segments de droites 2D,
- des rectangles 2D à cotés verticaux et horizontaux.
b) Implanter une méthode permettant de calculer le code de Cohen-Sutherland associé à une position vis à vis d'un rectangle.
c) Implanter une méthode permettant de calculer l'abscisse de l'intersection d'une droite horizontale avec la droite supportée par un segment.
d) Implanter une méthode permettant de calculer l'ordonnée de l'intersection d'une droite verticale avec la droite supportée par un segment.
e) Implanter une méthode de calcul du segment clippé d'un segment vis à vis d'un rectangle.
![]()
TP n°10: Découpage par l'algorithme de Cohen-Sutherland
Exercice n°1
Implanter et tester les questions du TD n°10.
Le TD a été réalisé en langage java. On pourra l'implanter au moyen de ce langage ou
bien l'adapter au langage C pour utiliser OpenGL pour l'affichage graphique.
On validera le fonctionnement de l'algorithme pour les cas particuliers où le segment
clippé est horizontal ou vertical, partiellement inclu, totalement inclu ou totalement
exclu du rectangle de clipping.
Exercice n°2
Généraliser l'algorithme de Cohen-Sutherland pour le clipping de segments de droites 2D dans un rectangle 2D au clipping de segments de droites 3D dans un parallélipipède rectangle 3D.
![]()
TD n°11: Remplissage d'une facette triangulaire
Le but du TD est de développer une méthode de remplissage d'une facette triangulaire
2D définie par ses trois sommets.
La technique utilisée consiste:
- à trier les 3 sommets par ordre d'ordonnée croissante,
- à déterminer si le sommet d'ordonnée intermédiaire est situer à droite ou à gauche de la droite passant par les sommets d'ordonnée minimum et maximum,
- à extraire les bords droit et gauche de la facette triangulaire (tableaux d'abscisses des pixels extrèmes droits et gauches sur chaque ligne horizontale de pixels d'ordonnée y comprise entre les ordonnées minimum et maximum de la facette,
- à dessiner chaque ligne de pixels d'ordonnée y entre les ordonnées minimum et maximum de la facette en itérant en abscisse entre les valeurs des bords gauche et droit.
![]()
TP n°11: Courbes et surfaces lissées
Si P0, P1, P2, P3, ..., Pn sont les n+1 sommets d’une ligne brisée. La courbe de Bézier définie par ces sommets (points de contrôle) est calculée au moyen de l'équation paramétrique suivante:
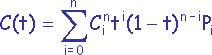 , t compris
entre 0 et 1.
, t compris
entre 0 et 1.
a) Soit la suite ordonnée de 8 sommets Pi suivante:
- {-3.0,-3.0,-3.0}
- {-2.0,3.0,1.0}
- {2.0,-3.0,-2.0}
- {3.0,3.0,-3.0}
- {-2.0,-1.0,2.0}
- {3.0,-3.0,-1.0}
- {2.0,3.0,3.0}
- {0.0,0.0,0.0}
Implanter le dessin de la courbe de Bézier générée à partir de ces sommets (calcul d'une courbe de nb points à partir d'un ensemble de n+1 points de contrôle).
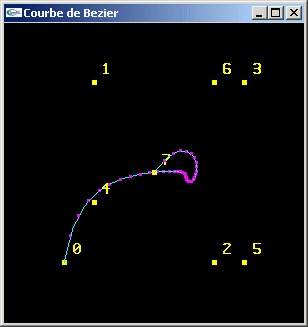
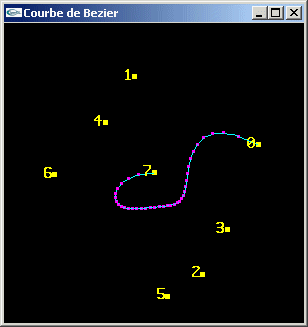
b) On souhaite vérifier expérimentalement si les courbes de Bézier sont compatibles avec les rotations.
- On considère la courbe de Bézier C1 obtenue par une rotation R quelconque de la courbe C générée à la question (a).
- On considère la courbe de Bézier C2 céée au moyen des sommets Pi transformés par la rotation R.
La courbe C1 est-elle égale à la courbe C2?
![]()