Sujets et Corrections
de TD et TP
![]()
TD n°1
Création de scènes
en VRML 1.0
TD n°2
Premières scènes
OpenGL
TP n°1
Implantation
de fichiers VRML
Implantation
de programmes
OpenGL
TD n°3
Modélisation
par facettes
en OpenGL
TD n°4
Modélisation
par facettes
en OpenGL
TP n°3
Gestion de caméras
en OpenGL
TD n°5
Caméras, lumières
et matériaux VRML
TP n°4
Matériaux
et lumières
en OpenGL
TD n°6
Calculs mathématiques
pour l'illumination
des objets
TP n°6
Transformations
géométriques
pour la visualisation
TD n°8
Clipping
par l'algorithme
de Cohen-Sutherland
TP n°7
Remplissage
de cercles et
de triangle
TD n°9
Quelques problèmes
mathématiques liés
au lancer de rayons
TP n°8
Plaçage de texture
en OpenGL
TD n°10
Calcul d'une
courbe de Bézier
TP n°9
Fonctions
pour le lancer
de rayons
Fichier
zip |
Dernière modification
02/12/09 16:44:37
TD n°1 : Création de scènes en VRML 1.0
(1) Programmer en VRML la scène suivante sans utiliser le nœud
Separator ailleurs que pour le Separator d'encadrement global du fichier:
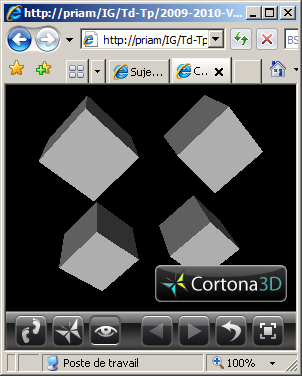
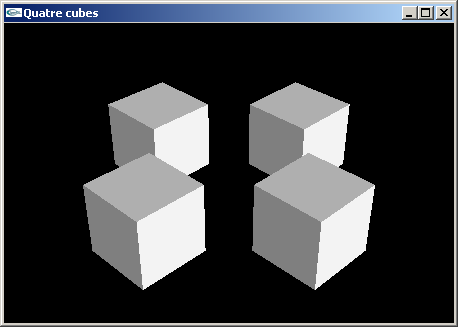
Quatre cubes de coté 2.0 aux positions (2.0,0.0,2.0), (2.0,0.0,-2.0), (-2.0,0.0,2.0) et
(-2.0,0.0,-2.0).
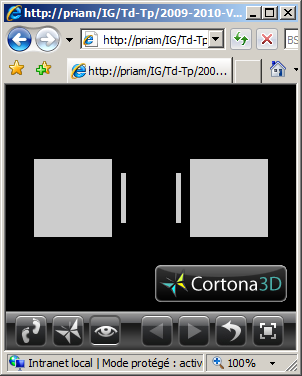

(2) Reprogrammer en VRML la scène de la question (1) de telle manière que les cubes aient une de leurs faces orientée vers l'origine du repère.
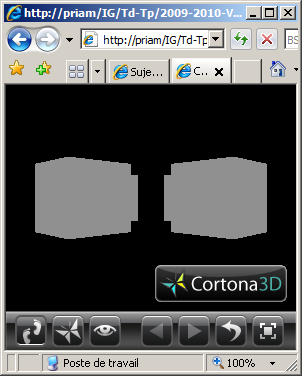
(3) Reprogrammer en VRML la scène de la question (2) en utilisant le nœud Separator pour rendre les objets indépendants les uns des autres et simplifier l'écriture du fichier scène.
(4) Programmer une scène en VRML en plaçant 3 cubes de coté 2.0 aux 3 sommets d'un
triangle équilatéral défini avec les caractéristiques suivantes:
- rayon 1.5,
- centré sur l'origine,
- plongé dans le plan xOz.
Les 3 cubes présentent une de leurs faces orientée vers l'origine.
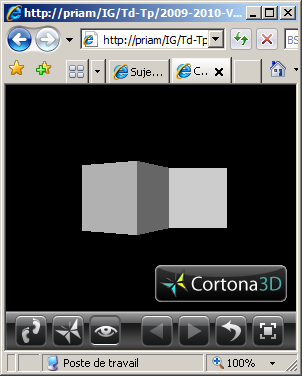
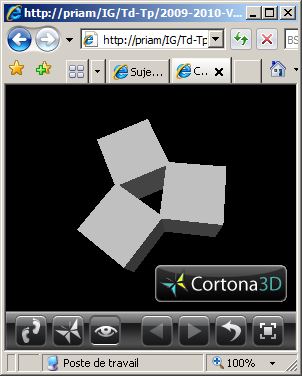
(5) Programmer la scène VRML modélisant un bras robot simplifié composé d'un
avant-bras et d'un bras.
L'avant-bras est articulé pour que sa base puisse tourner autour de l'axe Oy d'un angle
r1. Il s'agit d'un parallélépipède rectangle de dimension (3.0,1.0,1.0).
Le bras est articulé autour de l'axe y au bout de l'avant bras pour un angle r2. Il
s'agit d'un parallélépipède rectangle de dimension (3.0,0.8,0.8).
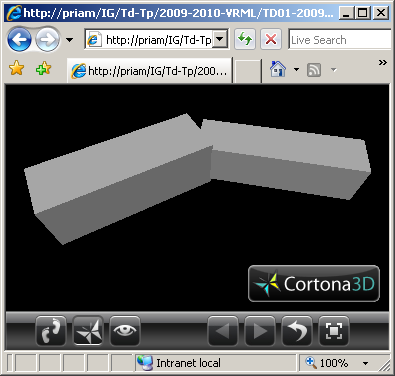
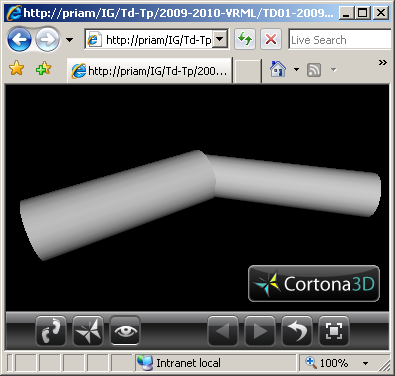
(6) Modifier le fichier VRML de l'exercice n°5 en remplaçant les parallélépipèdes par des cylindres de tailles équivalentes.
![]()
TD n°2: Premières scènes OpenGL
Exercice 1
Implanter en OpenGL les questions n°3 et n°4 du TD n°1.
Question n°3

Question n°4
Exercice 2
Implanter en OpenGL les questions n°5 et n°6 du TD n°1.
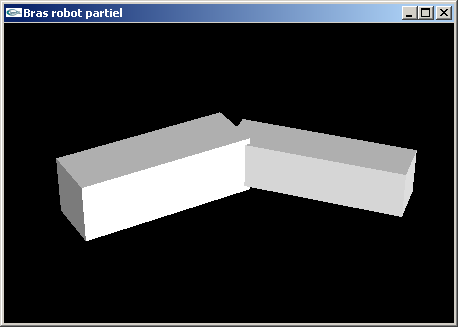
Question n°5
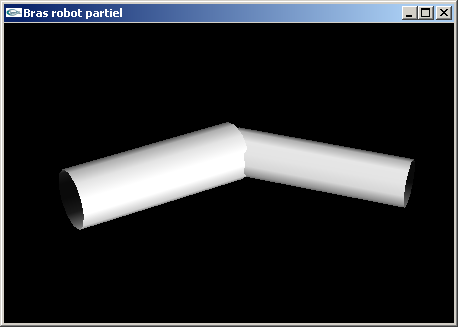
Question n°6
Exercice 3
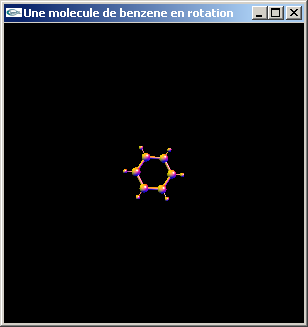
Implanter en OpenGL une fonction de dessin d'une molécule de Benzène (C6H6).
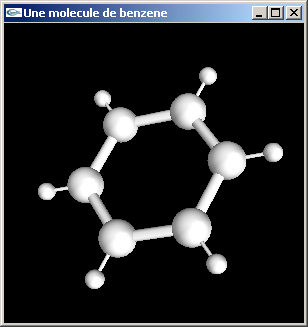
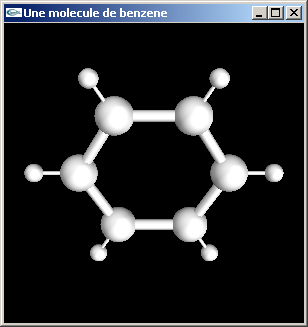
Les atomes de carbone (atome centraux) ont un rayon égal à 0.5.
Les liaisons entre 2 atomes de carbone ont pour longueur (centre à centre) 2.0 et pour
rayon 0.15.
Les atomes d'hydrogène ont un rayon égal à 0.25.
Les liaisons entre atome de carbone et d'hydrogène ont pour longueur (centre à centre)
1.2 et pour rayon 0.05.
La molécule est centrée sur l'origine et placée dans le plan xOy.
Solutions
![]()
TP n°1 : Premières implantations en VRML et en OpenGL
Exercice n°1 (VRML)
Les viewers VRML disponibles sont:
- Un plugin Internet Explorer/Netscape Navigator (Cortona Player)
- Une application de visualisation (Scene Viewer)
(a) Implanter les questions n°3 et n°4 du TD n°1.
(b) Implanter les questions n°5 et n°6 du TD n°1.
Exercice n°2 (OpenGL)
Création d'un projet Visual C++ permettant la compilation OpenGL:
- Les fichiers d'inclusion (nécessaires à la compilation) spécifiques à OpenGL sont GL/gl.h et GL/glu.h ainsi que GL/glut.h si GLUT est utilisé.
- Les librairies d'édition de liens (nécessaires à la création de l'exécutable) spécifiques à OpenGL sont OpenGL32.lib et glu32.lib ainsi que glut32.lib si GLUT est utilisé.
- Les dll (nécessaires à l'exécution) spécifiques à OpenGL sont OpenGL32.dll et glu32.dll ainsi que glut32.dll si GLUT est utilisé.
Seul GLUT n'est pas installé lors de l'installation de Visual C++. Il est
nécessaire de se procurer les fichiers .h, .lib et .dll lui
correspondant puis de les installer.
Les librairies OpenGL32.lib et glu32.lib spécifient des fonctions situées dans
OpenGL32.dll et glu32.dll.
Suivant la manière avec laquelle Visual C++ à été installé, il pourra être nécessaire (ou non) de spécifier les fichiers .lib d'OpenGL dans les options d'édition de lien.
Si gcc sous Linux est utilisé, Mesa3D devrait avoir été installé au
cours de l'installation des outils de développement (gcc). S'il ne l'est pas, ou si l'on
constate l'absence de GLUT, ou si l'on souhaite utiliser une version plus récente que
celle disponible (en septembre 2009, la version la plus récente disponible de Mesa3D est
la version 7.5.1 qui est compatible OpenGL 2.1), il sera nécessaire de télécharger et d'installer (compilation puis
installation, une archive pour OpenGL, une archive pour GLUT et une archive pour des
exemples) la version souhaitée.
Pour l'édition de lien d'un exécutable OpenGL & GLUT, il est nécessaire de
spécifier les librairies GL, GLU et glut dans la ligne de commande de compilation.
(a) Télécharger le programme source exemple suivant : GetConfig.cpp. Ce programme a pour but
d'initialiser OpenGL pour en extraire et afficher les informations de version.
Réaliser en la compilation et l'exécution.
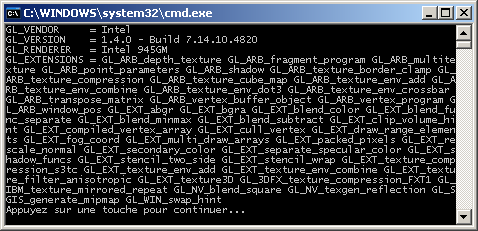
Exécutable compilé avec Visual C++ et
exécuté avec l'OpenGL du système d'exploitation
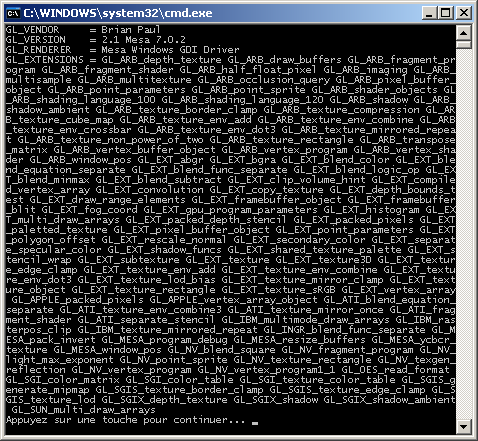
Exécutable compilé avec Visual C++ et
exécuté avec l'OpenGL Mesa3D version 7.0.2
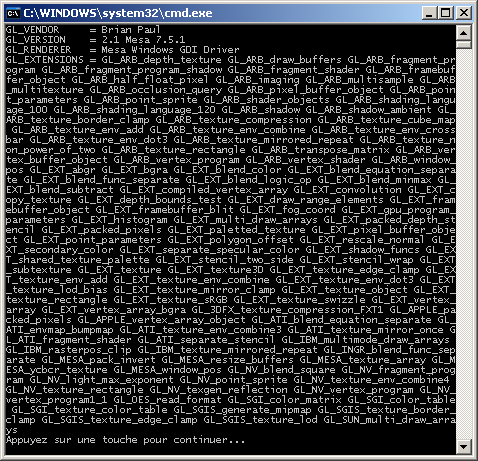
Exécutable compilé avec Visual C++ et
exécuté avec l'OpenGL Mesa3D version 7.5.1
b) Recommencer la procédure de test avec le fichier source suivant: Animation2009-2010.cpp.
Ce programme utilise OpenGL et GLUt pour afficher une scène 3D simple avec animation,
matériel et lumières, caméra, ...
Cet exemple pourra être utilisé pour les TPs suivants comme base de travail et être
adapté à d'autres affichages.


![]()
TP n°2 : Programmation OpenGL
Spécifications de GLUt version 3
Exercice n°1
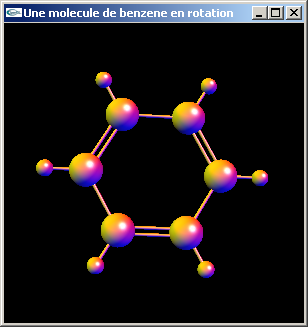
a) En adaptant le programme Animation2009-2010.cpp du TP n°1, implanter l'exercice du TD n°2 pour la modélisation et le dessin d'une molécule de benzène.
La fonction suivante pourra être utilisée pour modéliser un cylindre de hauteur h, de rayon r, de facteurs de facettisation n et m, centré sur l'origine et orienté selon l'axe y.
void cylindre(double h,double r,int n,int m) {
glPushMatrix();
glRotatef(90.0F,1.0F,0.0F,0.0F);
glTranslatef(0.0F,0.0F,-h/2);
GLUquadricObj *qobj = gluNewQuadric();
gluQuadricDrawStyle(qobj,GLU_FILL);
gluCylinder(qobj,r,r,h,n,m);
gluDeleteQuadric(qobj);
glPopMatrix();
}
b) Modifier la modélisation de la molécule de benzène de la question précédente
pour que les liaisons carbone-carbone soient alternativement des liaisons simples et des
liaisons doubles (voir figure ci-dessous).
Les cylindres modélisant ces liaisons auront pour rayon 0.05 (comme les liaisons
carbone-hydrogène). Dans le cas des liaisons doubles, les deux cylindres de modélisation
seront écartés de 0.1.

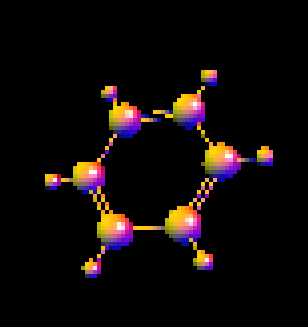
c) Définir et tester différentes alternatives (3 possibilités) permettant d'afficher la molécule en gros plan de manière à la visualiser avec précision.
Exercice n°2
a) Programmer la modélisation et l'affichage d'un tétraèdre modélisé par cylindres et sphères comme représenté sur la figure ci-dessous.
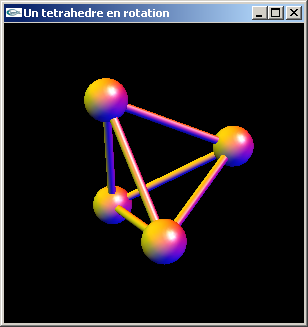
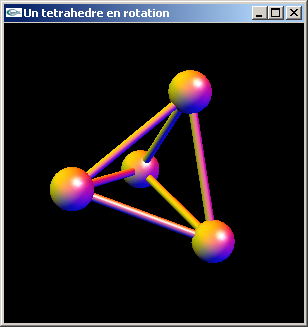
Les caractéristiques du tétraèdre sont les suivantes:
- Il est centré sur l'origine du repère.
- Une de ses faces est définie dans le plan xy.
- Ses sphères sont à une distance de sqrt(8.0) de l'origine.
- Ses sphères sont à une distance de sqrt(12.0) les unes des autres.
- L'une des sphères situées dans le plan xy est en position (2.0, 0.0,
-sqrt(0.5)).
- Les sphères ont pour rayon 0.5.
- Les cylindres ont pour rayon 0.1.
Solutions
GLUT |
||
| Benzène (question 1a) | ||
| Benzène (question 1b) | ||
| Benzène (question 1c version 1) | ||
| Benzène (question 1c version 2) | ||
| Benzène (question 1c version 3) | ||
| Tetraèdre | ||
![]()
TD n°3 : Modélisation par facettes en OpenGL
Exercice n°1
a) Modéliser par facettes un cube de coté 1.0 centré sur l'origine du repère de modélisation.
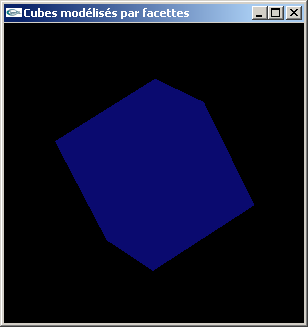

Lumières colorées et lumières blanches
b) Modifier la modélisation de la question précédente pour ajouter la gestion des normales.
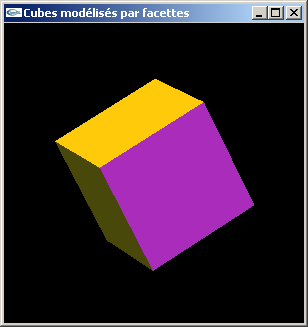
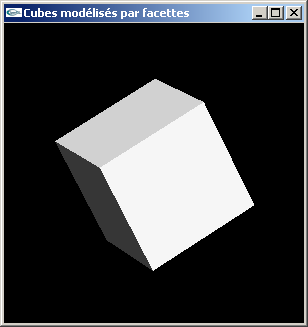
Lumières colorées et lumières blanches
Solution
GLUT |
||
| Cubes par facettes | ||
![]()
Exercice n°1 : Modélisation par facettes en OpenGL
Soit l'équation paramétrique de la bille de rayon r centrée sur le point de
coordonnées (cx,cy,cz):
t est un angle représentant la latitude. u est un angle représentant la longitude.
| t appartient à [-p/2,p/2] u appartient à [0,2p] |
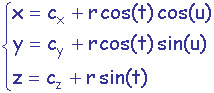 |
Développer une fonction de modélisation d'une sphère de rayon r, centrée sur
l'origine du repère de modélisation.
Cette fonction sera munie de la gestion des normales. Elle permettra de choisir les
niveaux de facettisation en longitude et en latitude.
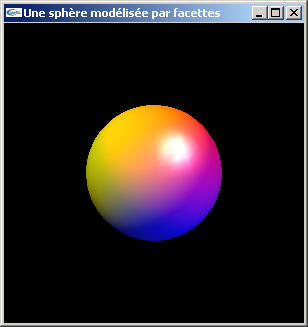

Lumières colorées et lumières blanches
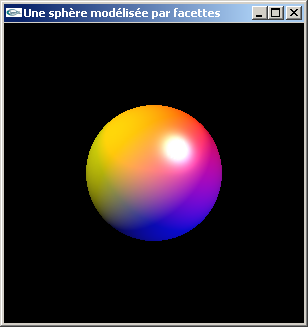
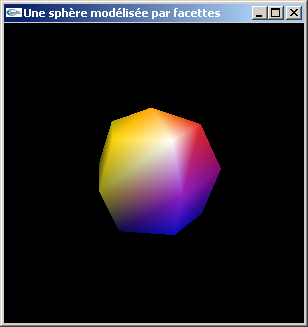
Avec beaucoup et peu de facettes
Solutions
GLUT |
||
| Sphère par facettes | ||
![]()
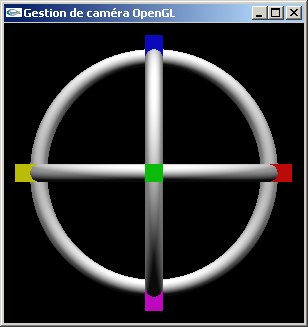
TP n°3 : Caméras OpenGL
Le fichier SceneOpenGL.cpp contient une fonction de dessin de scène. Celle-ci est prototypée dans le fichier SceneOpenGL.h. La scène modélisée occupe un volume approximativement sphèrique de rayon 12.0. Les objets jaune et rouge sont orientés en x. Les objets bleu et magenta sont orientés verticalement (en y). Les objets vert et cyan sont orientés en z.
Le but de l'exercice est de visualiser cette scène en gros plan dans une fenêtre d'affichage OpenGL.
Question n°1
Télécharger le fichier CameraOpenGL.cpp. Ce fichier utilise les deux fichiers précédents pour créer une application OpenGL + GLUt. La scène est "affichée", mais la fonction reshape étant incomplète, l'affichage est tout à fait incorrecte.
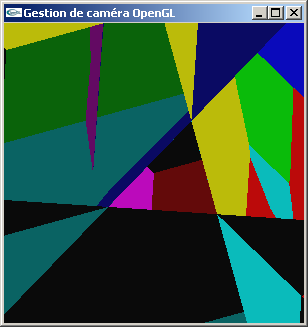
Complèter la fonction reshape pour obtenir un affichage en gros plan en projection orthographique selon l'axe -z. La scène est dessinée centrée sur l'origine.

Question n°2
Changer la caméra de la question n°1 pour lui substituer une caméra de visualisation
en perspective placée en position (1000.0, 1000.0,1000.0) tout en conservant la scène en
gros plan.
On s'efforcera de calculer a priori le bon angle d'ouverture.

Question n°3
Dans les questions suivantes, tester les conséquences d'un mauvais choix de cmin et
cmax dans le paramètrage de la fonction gluPerspective.
Tester l'influence des 7ème, 8ème et 9ème paramètre de la fonction GluLookAt sur
l'orientation de la scène.
a) Déplacer la caméra de la question n°2 pour l'amener en position (100.0,
100.0,100.0).
b) Déplacer de nouveau la caméra vers la position (20.0,20.0,20.0).
c) Déplacer encore une fois la caméra vers la position (10.0,10.0,10.0).
d) Déplacer une dernière fois la caméra vers la position (5.0,5.0,5.0).
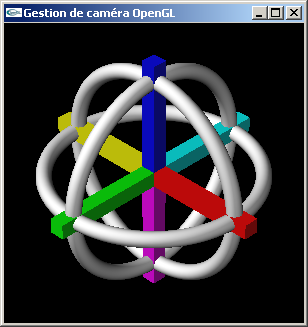 Question (a) |
 Question (b) |
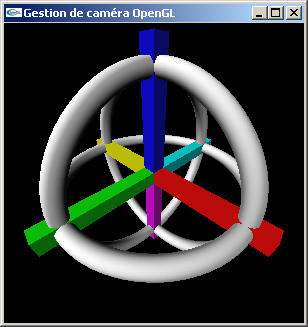 Question (c) |
|
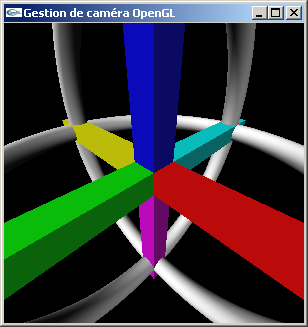 Question (d) |
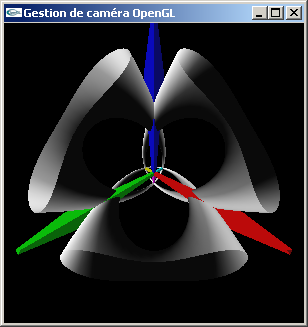 Question (d) |
Question n°4
Reprendre la question n°3b en ne s'autorisant plus l'utilisation de la fonction gluLookAt.
Solutions
![]()
TD n°5 : Caméra, lumières et matériaux en VRML
Question n°1
a) Définir une caméra de visualisation en perspective placée en position (0.0,0.0,10.0) orientée vers l'origine du repère.

b) Déplacer cette caméra vers la position (10.0,0.0,10.0) tout en la conservant orientée vers le point de coodonnées (0.0,0.0,0.0).
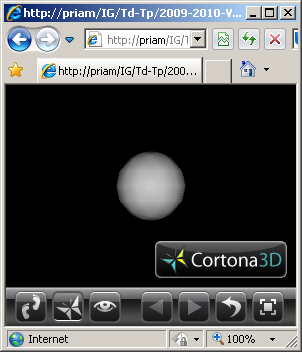
c) Déplacer une dernière fois cette caméra vers la position (10.0,10.0,10.0) tout en conservant son orientation vers l'origine.

Question n°2
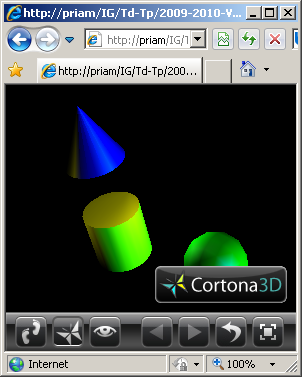
La caméra de l'exercice n°1 visualise la scène composée de quatre objets définis
selon les caractéristiques suivantes:
- un cube canonique diffusant en rouge en position (2.0,2.0,0.0),
- une sphère canonique diffusant en vert en position (2.0,-2.0,0.0),
- un cone canonique diffusant en bleu en position (-2.0,2.0,0.0),
- un cylindre canonique diffusant en jaune en position (-2.0,-2.0,0.0).
- Le matériel des quatre objets est réfléchissant en blanc avec une
réflectivité de 0.5.
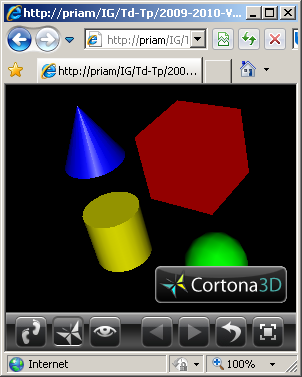
Question n°3
Tester successivement la scène de la question n°2 sous les éclairages suivants:
a) Une lumière ponctuelle blanche est placée en position (0.0,0.0,0.0).
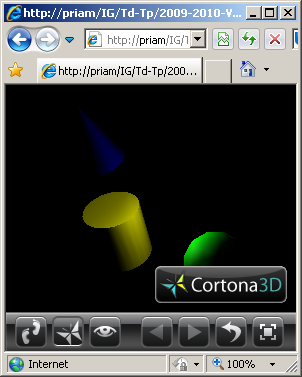
b) Une lumière directionnelle cyan éclaire la scène depuis la droite.

c) Un spot jaune est placé en position (-12.0,0.0,10.0) et est orienté vers le point de coordonnées (-2.0,0.0,0.0) avec une ouverture de 0.15 radians.
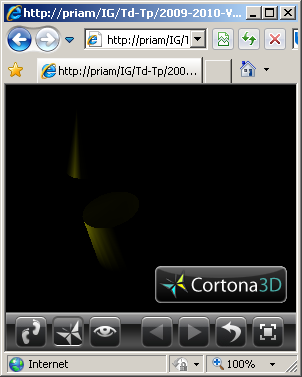
d) Les trois lumières des questions a), b) et c) sont définies.
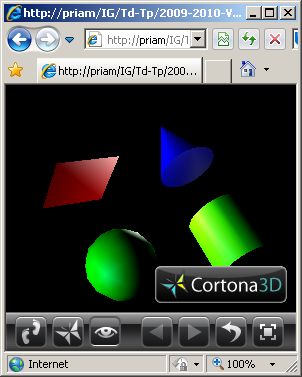
Solutions
![]()
TP n°4 : Lumières et matériaux en OpenGL
Réaliser l'implantation en OpenGL + GLUt des questions du TD n°5.
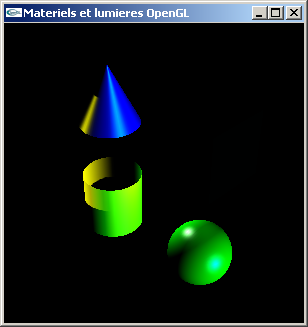
Avec les trois lumières
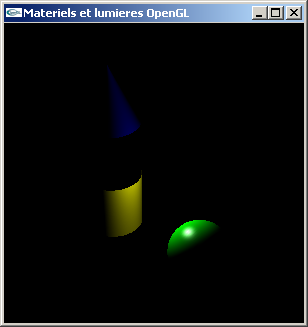

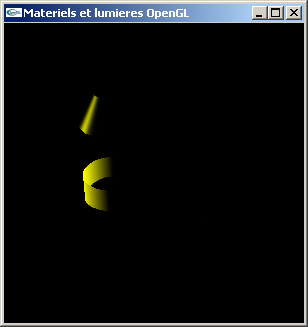
Contributions individuelles des trois lumières
Solution
![]()
TD n°6 : Calculs mathématiques pour l'illumination des objets
Le TD est réalisé en langage Java.
Question n°1
L'exercice consiste à évaluer la quantité d'énergie diffusée par une surface "colorée" éclairée par une lumière directionnelle colorée.
a) Développer les classes Material.java, Normale.java et LumiereDirectionnelle.java minimales nécessaires (variables membres et constructeurs), ainsi que les classes utilitaires qu'elles requièrent, permettant d'instancier les objets à gérer pour résoudre la question n°1.
b) Developper une méthode de calcul de l'énergie diffusée par une surface sous l'éclairage d'une lumière directionnelle. On utilisera la formule de Lambert.
Question n°2
L'exercice consiste à évaluer la quantité d'énergie diffusée par une surface "colorée" éclairée par une lumière ponctuelle colorée.
a) Développer les classes Position.java et LumierePonctuelle.java minimales nécessaires (variables membres et constructeurs), ainsi que les classes utilitaires qu'elles requièrent, permettant d'instancier les objets à gérer pour résoudre la question n°2.
b) Developper une méthode de calcul de l'énergie diffusée par une surface sous l'éclairage d'une lumière ponctuelle. On utilisera la formule de Lambert.
Solutions
![]()
Pour gérer les animations demandées, on pourra utiliser glutIdleFunc (programmation d'une tâche de fond) ou glutTimerFunc (programmation d'une fonction timer).
a) Le fichier ScenePourAnimation.cpp (décrit par le fichier d'entête ScenePourAnimation.h) contient une fonction void scene(int l) de modélisation d'une scène composée d'une surface plane carrée de diagonale (-10.0, 0.0, -10.0) - (10.0, 0.0, 10.0) sur laquelle sont posés aléatoirement 100 "poteaux" parallélipipédiques. L'éclairage de cette scène est activé/désactivé par le paramètre booléen l.

Implanter le dessin de cette scène par une caméra de visualisation en perspective placée en position (0.0, 0.5, 0.0) orientée selon la direction (0.0, 0.0, 1.0). L'ouverture verticale de la caméra est de 60°. Les plans cmin est cmax sont aux distances 0.01 et 100.0. La taille de la fenêtre d'affichage est 450 sur 200 pixels.
b) Modifier le programme précédent pour autoriser le déplacement de la caméra au moyen des touches up et down de manière à avancer et reculer dans la scène dans l'axe de la caméra.
c) Modifier le programme précédent pour autoriser l'utilisation des touches right et left de manière à faire tourner la caméra vers la droite et vers la gauche tout en continuant à pourvoir utiliser les touches up et down pour l'avancer et la reculer.

d) Modifier une nouvelle fois le programme précédent pour que l'utilisateur puisse utiliser la touche "Enter" pour activer la réalisation automatique d'un tour sur elle-même pour la caméra. Pendant le tour, celle-ci ne peut plus se déplacer. Après le tour elle s'immobilise avec la posture qu'elle avait avant de le débuter et peut de nouveau se déplacer.
e) Revenir à la version c) et modifier la scène pour transformer les poteaux en cylindres de rayon 0.05 et de hauteur 2.0 et gérer les déplacements de la caméra de manière qu'il lui soit impossible de traverser les poteaux ainsi modifiés (impossible de se rapprocher à une distance inférieure à 0.01 d'un poteau).


f) Modifier la scène pour que la lumière ponctuelle qui l'éclaire se déplace automatiquement pour décrire une trajectoire circulaire d'altitude (y) constante 1.0 centrée sur le point de coordonnées (0.0,1.0,0.0) et de rayon 5.0.
g) Modifier la scène pour y inclure un objet supplémentaire en déplacement. Cet objet est une sphère blanche de rayon 0.1 qui se déplace pour matérialiser la lumière ponctuelle en mouvement. Gérer l'affichage de cette sphère de manière qu'elle apparaisse illuminée par une lumière lui étant extérieure.

Solutions
GLUT |
||
| Questions (a), (b), (c) et (d) avec glutIdleFunc | ||
| Questions (a), (b), (c), (e), (f) et (g) avec glutIdleFunc | ||
| Questions (a), (b), (c), (e), (f) et (g) avec glutTimerFunc | ||
![]()
TD n°7 : Coordonnées homogènes
Le TD est réalisé en langage Java.
Exercice n°1
a) Développer une classe CoordonneesHomogenes3D permettant de stocker des coordonnées homogènes dans un espace à 3 dimensions.
b) Dériver la classe du (a) en une classe Position3D permettant de stocker des positions dans un espace 3D.
c) Dériver la classe du (a) en une classe Direction3D permettant de stocker des directions dans un espace 3D.
Exercice n°2
a) Développer une classe TransformationGeometrique3D permettant de stocker des transformations géométriques génériques en coordonnées homogènes dans un espace à 3 dimensions.
b) Dériver la classe du (a) en une classe Translation permettant de stocker des translations dans un espace à 3 dimensions.
c) Dériver la classe du (a) en une classe Rotation permettant de stocker des rotations (rotation d'angle arbitraire autour d'un axe arbitraire non nul passant par l'origine) dans un espace à 3 dimensions.
d) Dériver la classe du (a) en une classe Scale permettant de stocker des zooms dans un espace à 3 dimensions.
Exercice n°3
Modifier les classes précédentes pour y inclure les méthodes permettant de réaliser la transformation d'une position par une transformation géométrique, la transformation d'une direction par une transformation géométrique, la composition de transformations géométriques.
Solutions
![]()
TP n°6 : Transformations géométriques pour la visualisation
Le fichier AffichageEcranOrthographique.cpp donne un exemple de programme OpenGL où la caméra virtuelle de visualisation est définie selon les caractéristiques suivantes:
- La scène modélisée est affichée en projection parallèle orthographique selon l'axe de projection -z.
- L'origine du repère de modélisation est projeté au centre de la fenêtre.
- Un repère virtuel d'affichage est défini de manière qu'une distance de 1.0 dans le repère de modélisation se traduise par une distance de 1 pixel à l'écran (i.e. les coordonnées de modélisation sont comptées directement en pixels écran).
La scène affichée est constituée de lignes horizontales ou verticales (Enter pour switcher) de 1 pixel d'épaisseur séparées de 2.0 en coordonnées de modélisation et donc de 2 pixels en coordonnées écran ce qui conduit à une alternance de lignes de pixels rouges et de lignes de pixels noirs.
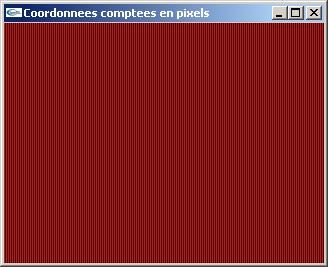

On pourra s'inspirer de cet exemple pour la suite du TP.
Exercice n°1
Les lignes de code suivantes définissent un objet en "fil de fer" par la donnée de la position (en coordonnées homogènes) de ses npos sommets et la donnée des nind couples d'indices, dans le tableau des sommets, définissant les arêtes.
typedef float coordonneesHomogenes3D[4];
typedef float transformationGeometrique3D[4][4];
static int npos = 10;
static int nind = 15;
static coordonneesHomogenes3D pos[] =
{ { 2.0, 0.0, 3.0, 1.0 },
{ 2.0, 3.0, 3.0, 1.0 },
{ 0.0, 5.0, 3.0, 1.0 },
{ -2.0, 3.0, 3.0, 1.0 },
{ -2.0, 0.0, 3.0, 1.0 },
{ 2.0, 0.0,-3.0, 1.0 },
{ 2.0, 3.0,-3.0, 1.0 },
{ 0.0, 5.0,-3.0, 1.0 },
{ -2.0, 3.0,-3.0, 1.0 },
{ -2.0, 0.0,-3.0, 1.0 } };
static int ind[][2] =
{ { 0, 1 },
{ 1, 2 },
{ 2, 3 },
{ 3, 4 },
{ 4, 0 },
{ 5, 6 },
{ 6, 7 },
{ 7, 8 },
{ 8, 9 },
{ 9, 5 },
{ 0, 5 },
{ 1, 6 },
{ 2, 7 },
{ 3, 8 },
{ 4, 9 } };

Le but de l'exercice est d'afficher cet objet en projection parallèle orthographique en programmant soit-même la transformation géométrique de visualisation qui permet de définir la position Pc de la caméra de visualisation (par exemple (10.0, 6.0, 10.0)) et la position Pv d'un point visé (par exemple (0.0, 2.5, 0.0)) en conservant vertical à l'écran l'axe y (voir chapitre de cours).
La matrice de transformation correspondante est la suivante:
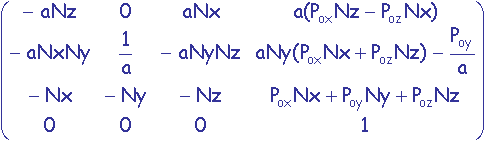
où ![]() est le
vecteur normé défini par la direction Pc vers Pv et a =
est le
vecteur normé défini par la direction Pc vers Pv et a = 
Travail à réaliser
- Pc et Pv sont donnés (éventuellement modifiables dynamiquement au clavier).
- La matrice de transformation de visualisation est calculée.
- Les coordonnées de l'objet sont transformées par la matrice de transformation de visualisation (voir chapitre de cours).
- Les coodonnées ainsi obtenues sont utilisées pour l'affichage.
Le programme OpenGL, qui DOIT intégrer sa propre caméra, sera conçu avec cette caméra configurée en projection parallèle orthographique pour ne pas déformer les coordonnées écrans calculées et utilisées.
Exercice n°2
Cet exercice reprend l'exercice n°1 pour transformer l'affichage en projection parallèle orthographique en un affichage en perspective.

La matrice de transformation à utiliser est la suivante (voir chapitre de cours):

où d est la position en -z (donc d est de valeur négative) de l'écran virtuel de projection (par exemple d = -15.0).
Les coordonnées en x et en y obtenues après transformation par cette matrice devront être divisées par w pour achever la mise en perspective de manière à obtenir les coordonnées x et y écran définitives.
![]()
TD n°8: Clipping par l'algorithme de Cohen-Sutherland
L'implantation est réalisée en langage java.
a) Définir trois classes de stockage pour:
- des positions en deux dimensions,
- des segments de droites 2D,
- des rectangles 2D à cotés verticaux et horizontaux.
b) Implanter une méthode permettant de calculer le code de Cohen-Sutherland associé à une position vis à vis d'un rectangle.
c) Implanter une méthode permettant de calculer l'abscisse de l'intersection d'une droite horizontale avec la droite supportée par un segment.
d) Implanter une méthode permettant de calculer l'ordonnée de l'intersection d'une droite verticale avec la droite supportée par un segment.
e) Implanter une méthode de calcul du segment clippé d'un segment vis à vis d'un rectangle.
![]()
TP n°7 : Rastérisation de surfaces
Pour ces exercices, on pourra de nouveau utiliser le code source AffichageEcranOrthographique.cpp pour dessiner en coordonnées de modélisation comptées en pixels.
Exercice n°1 : Rastérisation d'un cercle
On considère un cercle de rayon r entier centré sur l'origine.
a) Implanter une fonction de traçage des pixels du bord de ce cercle avec utilisation de l'algorithme de Bresenham.
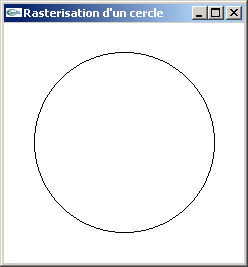
b) Implanter une fonction de remplissage des pixels de ce cercle.

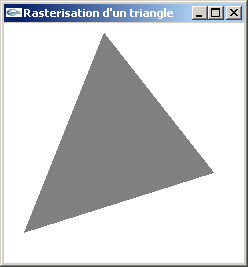
Exercice n°2 : Rastérisation d'un triangle
On considère un polygone triangulaire quelconque.
a) Implanter une fonction de traçage des pixels du bord de ce triangle avec utilisation de l'algorithme de Bresenham.
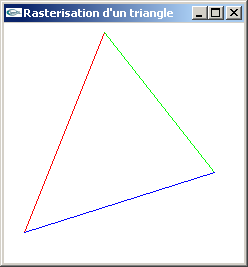
b) Implanter une fonction de remplissage des pixels de ce triangle.
Solutions
![]()
TD n°9: Quelques problèmes mathématiques liés au lancer de rayons
Le TD est réalisé en langage C. Les structures suivantes devront être utilisées:
- typedef struct position {
double x;
double y;
double z;
double t; } position; - typedef struct direction {
double x;
double y;
double z;
double t; } direction; - typedef struct sphere {
position centre;
double rayon; } sphere; - typedef struct rayonLumineux {
position origine;
direction direction; } rayonLumineux;
a) Implanter une fonction permettant de tester l'existence d'une intersection entre un rayon lumineux et une sphère.
b) Implanter une fonction permettant de déterminer, si elle existe, la distance entre le point d'émission d'un rayon lumineux et l'intersection entre ce rayon et une sphère.
c) Implanter une fonction permettant de calculer la direction du rayon réfléchi créé par un rayon incident à l'interface entre deux milieux.
d) Implanter une fonction permettant de calculer la direction du rayon transmis créé par un rayon incident à l'interface entre deux milieux.
![]()
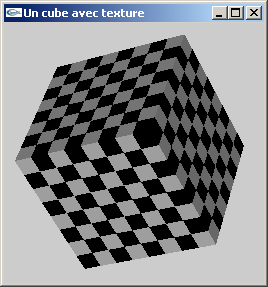
TP n°8 : Plaçage de texture bitmap 2D en OpenGL
La portion de code suivante crée un tableau d'octets représentatif d'une bitmap RGB de 8x8 pixels représentant un damier noir et blanc.
GLubyte *makeImage(void) {
GLubyte *tab =(GLubyte *) malloc(8*8*3*sizeof(GLubyte));
GLubyte *t = tab;
for ( int i = 0 ; i < 8 ; i++ )
for ( int j = 0 ; j < 8 ; j++ ) {
t[0] = t[1] = t[2] = ( (i+j)%2 ) ? 0x00 : 0xFF;
t += 3; }
return(tab);
}
a) Reprendre le cube modélisé par facettes lors du TD n°3 pour le texturer au moyen d'une image bitmap créée par cette fonction.
b) Cette fonction peut être utilisée pour modéliser par facettes une sphère:
#ifndef M_PI
#define M_PI 3.14159265358979323846264338327950288
#endif
void solidSphere(float rayon,int nlat,int nlon) {
for ( int i = 0 ; i < nlat ; i++ ) {
float a1 = -M_PI/2.0F + i*M_PI/nlat ;
float a2 = a1 + M_PI/nlat ;
float cs1 = cos(a1);
float cs2 = cos(a2);
float sn1 = sin(a1);
float sn2 = sin(a2);
glBegin(GL_QUAD_STRIP);
for ( int j = 0 ; j <= nlon ; j++ ) {
float a = j*2*M_PI/nlon;
float cs = cos(a);
float sn = sin(a);
float x1 = cs1*cs;
float z1 = cs1*sn;
float x2 = cs2*cs;
float z2 = cs2*sn;
glNormal3f(x1,sn1,z1);
glVertex3f(rayon*x1,rayon*sn1,rayon*z1);
glNormal3f(x2,sn2,z2);
glVertex3f(rayon*x2,rayon*sn2,rayon*z2); }
glEnd(); }
}
Adapter cette fonction la pour qu'elle intègre la création des coordonnées de texturage de manière à autoriser l'emploi de textures.

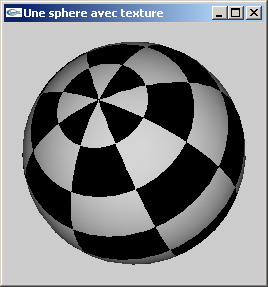
c) Les trois fichiers suivants:
sont des fichiers au format raw (RGB entrelacé, le nom du fichier indique la résolution).



Développer une fonction de chargement d'un tel fichier en mémoire.
Adapter le code source des questions a) et b) pour afficher le cube texturé avec l'image
contenue dans le fichier Image-256-256.raw
et la sphère texturée avec, au choix, soit l'image du fichier Terre-256-256.raw, soit celle du fichier Mars-256-128.raw.


Solutions
GLUt |
||
| Texturage d'un cube avec un damier | ||
| Texturage d'une sphère avec un damier | ||
| Texturage d'un cube avec un fichier raw | ||
| Texturage d'une sphère avec un fichier raw | ||
![]()
TD n°10: Calcul d'une courbe de Bézier
Le TD est réalisé en C.
On considère les types de données suivants:
typedef struct coord_3D {
GLfloat x,y,z,w; } coord_3D;
typedef struct lignePolygonale {
int n;
coord_3D *p; } lignePolygonale;
Développer une fonction de calcul de la lignePolygonale représentative
de la courbe de Bézier obtenue en considérant qu'une lignePolygonale définit ses points
de contrôle.
On passera en paramètre supplémentaire le nombre de points de définition de la courbe
de Bézier calculée.
On pourra utiliser le code suivant pour initialiser une lignePolygonale de 2 (à 8) points de contrôle:
static GLfloat pts[8][4] = {
{-3.0,-3.0,-3.0,1.0},{-2.0, 3.0, 1.0,1.0},
{ 2.0,-3.0,-2.0,1.0},{ 3.0, 3.0,-3.0,1.0},
{-2.0,-1.0, 2.0,1.0},{ 3.0,-3.0,-1.0,1.0},
{ 2.0, 3.0, 3.0,1.0},{ 0.0, 0.0, 0.0,1.0} };
static int aff = 2;
static
lignePolygonale pl = { aff,(coord_3D *) &pts[0][0] };


Solutions
![]()
TP n°9: Calcul de l'intersection entre une sphère et un rayon, des rayons réfléchi et transmis dans le cadre de l'implantation d'un algorithme de lancer de rayons
Le fichier RayTracing.zip contient un
programme de calcul et d'affichage de scènes représentées en lancer de rayons.
Ces scènes sont constituées exclusivement de sphères diffusantes, réfléchissantes et
transparentes. Elles sont éclairées par des lumières ponctuelles ou directionnelles.
Un certain nombre de fonctions ont été vidées de leur contenu.
Le but du TP consiste à développer ces fonctions:
- Fichier RayTracing-Sphere.cpp :
- Test de l'existence d'une intersection entre un rayon lumineux et une sphère:
int intersection(rayonLumineux *rl,
sphere *sp); - Test de l'existence d'une intersection entre un rayon lumineux et une sphère et calcul
de la distance entre cet intersection, si elle existe, et l'origine du rayon lumineux:
int intersection(rayonLumineux *rl,
sphere *sp,
double *d);
- Test de l'existence d'une intersection entre un rayon lumineux et une sphère:
- Fichier RayTracing-Direction.cpp :
- Calcul de la direction du rayon réfléchi à l'interface entre deux matériaux:
void reflexion(direction *r,
direction *i,direction *n); - Test de l'existence du rayon transmis à l'interface entre deux matériaux, et calcul,
s'il y a transmission, de la direction de transmission:
int transmission(direction *t,
direction *i,direction *n,
double niSurnt); - Calcul du produit scalaire de deux directions:
double produitScalaire(direction *d1,direction *d2); - Normalisation d'une direction:
void normalise(direction *d); - Calcul et nomalisation de la direction définie entre deux positions:
void calculDirectionNormalisee(direction *d,
position *p1,position *p2);
- Calcul de la direction du rayon réfléchi à l'interface entre deux matériaux:
- Fichier RayTracing-Position.cpp :
- Calcul du carré de la distance entre deux positions:
double carreDistance(position *p1,position *p2); - Calcul du de la distance entre deux positions
double distance(position *p1,position *p2);
- Calcul du carré de la distance entre deux positions:


Solution
![]()
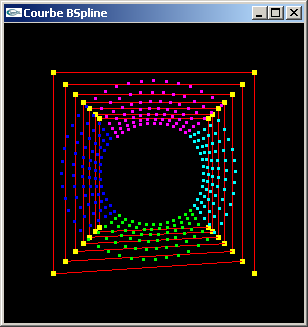
TD n°11: Les courbes BSplines
On considère les structures de données C suivantes:
typedef struct coord_3D {
GLfloat x,y,z,w; } coord_3D;
typedef struct lignePolygonale {
int n;
coord_3D *p; } lignePolygonale;
typedef float matrice[4][4];
Exercice n°1
Développer une fonction permettant de calculer la position du point P d'une BSpline
correspondant à une valeur de t.
Les données connues sont la matrice de base à utiliser, le vecteur géométrie
constituée des quatre points de contrôle et la valeur de t.
Exercice n°2
Développer une fonction de calcul de la lignePolygonale représentative
de la courbe de BSpline par morceaux obtenue en considérant qu'une lignePolygonale
définit ses points de contrôle.
Les données connues sont la matrice de base, la lignePolygonale des points de
contrôle et le nombre de points à créer sur la ligne polygonale lissée.
Application numérique
static coord_3D ptsi[28] = {
{-3.0,-3.0,-3.0,1.0},{-3.0, 3.0,-3.0,1.0},
{ 3.0, 3.0,-3.0,1.0},{ 3.0,-3.0,-3.0,1.0},
{-3.0,-3.0,-2.0,1.0},{-3.0, 3.0,-2.0,1.0},
{ 3.0, 3.0,-2.0,1.0},{ 3.0,-3.0,-2.0,1.0},
{-3.0,-3.0,-1.0,1.0},{-3.0, 3.0,-1.0,1.0},
{ 3.0, 3.0,-1.0,1.0},{ 3.0,-3.0,-1.0,1.0},
{-3.0,-3.0, 0.0,1.0},{-3.0, 3.0, 0.0,1.0},
{ 3.0, 3.0, 0.0,1.0},{ 3.0,-3.0, 0.0,1.0},
{-3.0,-3.0, 1.0,1.0},{-3.0, 3.0, 1.0,1.0},
{ 3.0, 3.0, 1.0,1.0},{ 3.0,-3.0, 1.0,1.0},
{-3.0,-3.0, 2.0,1.0},{-3.0, 3.0, 2.0,1.0},
{ 3.0, 3.0, 2.0,1.0},{ 3.0,-3.0, 2.0,1.0},
{-3.0,-3.0, 3.0,1.0},{-3.0, 3.0, 3.0,1.0},
{ 3.0, 3.0, 3.0,1.0},{ 3.0,-3.0, 3.0,1.0} };
static lignePolygonale pl = { 28,(coord_3D *) &ptsi[0] };
matrice nrubs = { -0.1667F, 0.5F, -0.5F, 0.1667F,
0.5F ,-1.0F, 0.5F, 0.0F,
-0.5F , 0.0F, 0.5F, 0.0F,
0.1667F, 0.6667F, 0.1667F,0.0F };
matrice catmullRom = { -0.5F, 1.5F,-1.5F, 0.5F,
1.0F,-2.5F, 2.0F,-0.5F,
-0.5F, 0.0F, 0.5F, 0.0F,
0.0F, 1.0F, 0.0F, 0.0F };

Solutions
![]()