Sujets et Corrections
de TD et TP
![]()
|
Fichier zip |
TD n°1 : Premières scènes OpenGL
Exercice n°1
(1) Programmer en OpenGL la scène suivante sous la forme d'une fonction C sans utiliser les fonctions
glPushMatrix et glPopMatrix ailleurs qu'en début et fin de fonction:
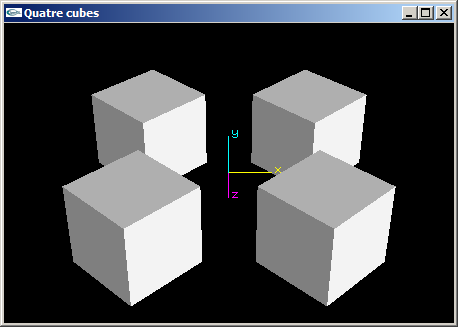
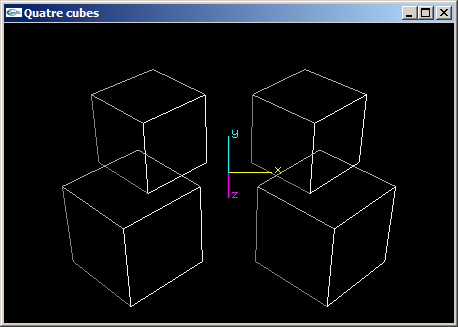
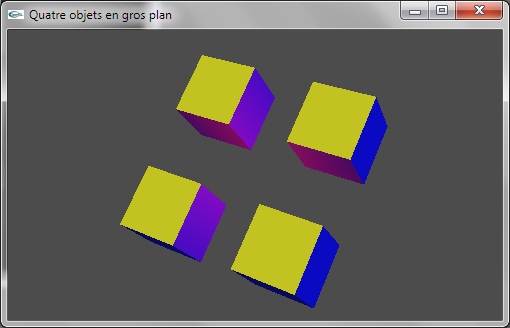
Quatre cubes de coté 2.0 aux positions (2.0,0.0,2.0), (2.0,0.0,-2.0), (-2.0,0.0,2.0) et (-2.0,0.0,-2.0).
(2) Reprogrammer en OpenGL la scène de la question (1) de telle manière que les cubes aient une de leurs faces orientée vers l'origine du repère.
(3) Reprogrammer en OpenGL la scène de la question (2) en utilisant les fonctions glPushMatrix et glPopMatrix pour rendre les objets indépendants les uns des autres et simplifier l'écriture de la fonction scène.
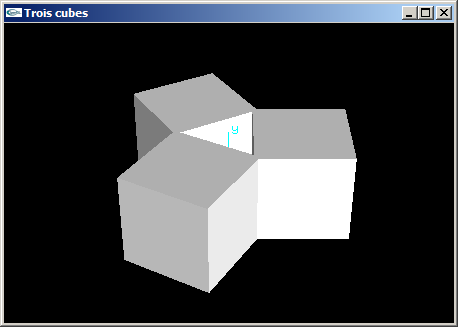
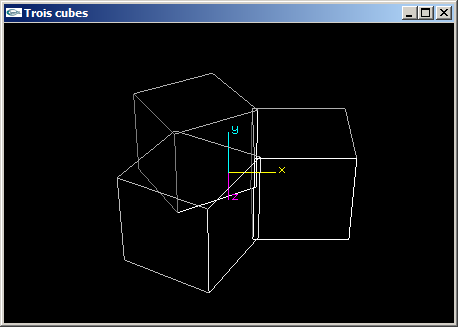
(4) Programmer une scène OpenGL en plaçant 3 cubes de coté 2.0 aux 3 sommets d'un triangle
équilatéral défini avec les caractéristiques suivantes:
- rayon 1.5,
- centré sur l'origine,
- plongé dans le plan xOz.
Les 3 cubes présentent une de leurs faces orientée vers l'origine.
Exercice n°2
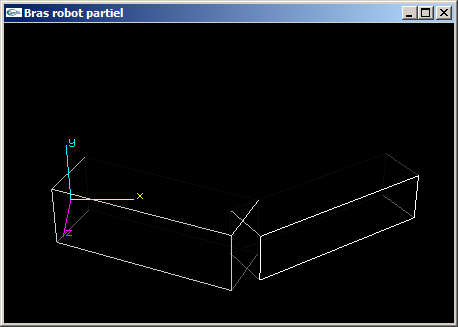
(1) Programmer la scène OpenGL modélisant un bras robot simplifié composé d'un avant-bras
et d'un bras.
L'avant-bras est articulé pour que sa base puisse tourner autour de l'axe Oy d'un angle r1. Il s'agit d'un
parallélépipède rectangle de dimension (3.0,1.0,1.0).
Le bras est articulé autour de l'axe y au bout de l'avant bras pour un angle r2. Il s'agit d'un parallélépipède
rectangle de dimension (3.0,0.8,0.8).

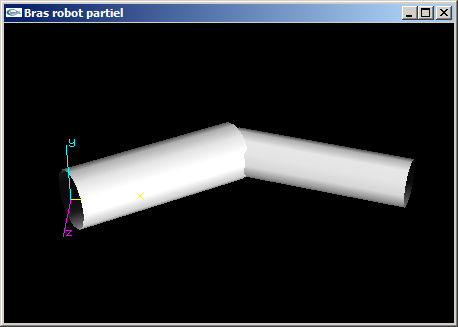
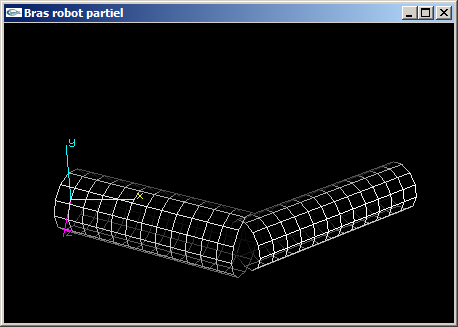
(2) Modifier la fonction OpenGL de l'exercice n°1 en remplaçant les parallélépipèdes par des cylindres de tailles équivalentes.
Exercice 3
a) Implanter en OpenGL une fonction de dessin d'une molécule de Benzène (C6H6).
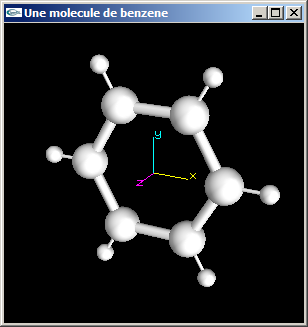
Les atomes de carbone (atome centraux) ont un rayon égal à 0.5.
Les liaisons entre 2 atomes de carbone ont pour longueur (centre à centre) 2.0 et pour rayon 0.15.
Les atomes d'hydrogène ont un rayon égal à 0.25.
Les liaisons entre atome de carbone et d'hydrogène ont pour longueur (centre à centre) 1.2 et pour
rayon 0.05.
La molécule est centrée sur l'origine et placée dans le plan xOy.
b) Modifier la modélisation de la molécule de benzène de la question précédente
pour que les liaisons carbone-carbone soient alternativement des liaisons simples et des liaisons doubles (voir
figure ci-dessous).
Les cylindres modélisant ces liaisons auront pour rayon 0.05 (comme les liaisons carbone-hydrogène).
Dans le cas des liaisons doubles, les deux cylindres de modélisation seront écartés de 0.1.

Solutions
| Quatre cubes (Question 3) |
| Trois cubes |
| Bras robot avec parallélépipèdes |
| Bras robot avec cylindres |
| Molécule de benzène |
![]()
TD n°2 : Modélisation par facettes
Exercice n°1
a) Modéliser par facettes un cube de coté c centré sur l'origine du repère de modélisation.
On ne générera pas les normales.
La fonction créée aura pour prototype:
void mySolidCube(double c);
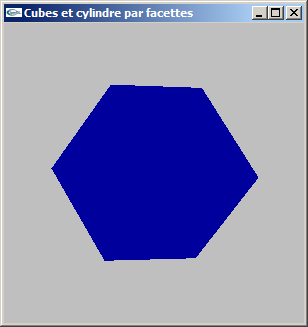
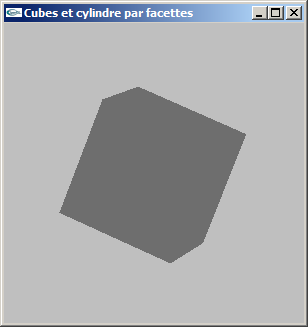
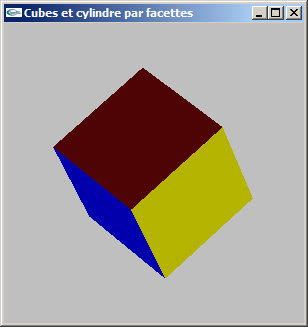
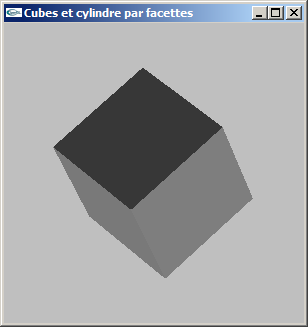
b) Modifier la modélisation de la question précédente pour ajouter
la gestion des normales.
Le but est de rendre possible les calculs d'éclairage.
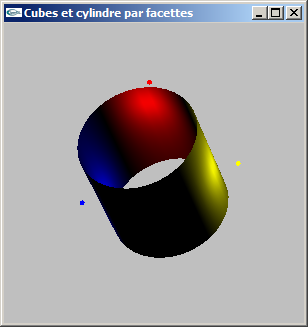
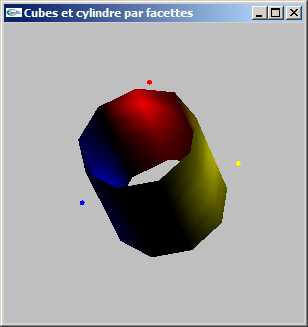
a) Modéliser par facettes un cylindre selon les caractéristiques suivantes:
- choix du rayon,
- choix de la hauteur,
- choix du nombre de facettes en découpage longitudinal pour une valeur entière ns,
- centré sur l'origine du repère de modélisation,
- axé selon y.
On ne modélisera pas les bases du cylindre, mais uniquement le tube.
La fonction créée aura pour prototype:
void mySolidCylinder(double hauteur, double rayon, int ns);
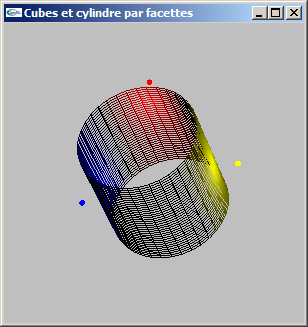
b) Ajouter un découpage latéral (selon l'axe y) pour une valeur nl.
Le prototype de la fonction devient:
void mySolidCylindre(double hauteur, double rayon, int ns, int nl);
Solutions
![]()
TD n°3 : Paramètrage numérique de caméras
Exercice n°1
a) On considère une caméra de visualisation en projection parallèle orthographique placée en position (0.0, 0.0,
0.0) orientée selon l'axe (0.0, 0.0, -1.0). On considère une scène centrée sur le point de coordonnées (0.0,
0.0, -100.0) et occupant un volume circulaire de rayon voisin de 10.0.
Quelle ouverture doit-on donner à cette caméra pour visualiser cette scène en gros plan dans la fenêtre d'affichage?
b) On considère une caméra de visualisation en projection en perspective placée en position (0.0, 0.0, 0.0) orientée
selon l'axe (0.0, 0.0, -1.0). On considère une scène centrée sur le point de coordonnées (0.0, 0.0, -100.0)
et occupant un volume circulaire de rayon voisin de 10.0.
Quelle ouverture doit-on donner à cette caméra pour visualiser cette scène en gros plan dans la fenêtre d'affichage?
Exercice n°2
Une caméra de visualisation en perspective OpenGL est obligatoirement placée en position (0.0, 0.0, 0.0) du repère de modélisation. Elle est obligatoirement orientée pour selon l'axe de projection (0.0, 0.0,-1.0).
a) On considère une scène modélisée au sein d'une fonction C de manière à être centrée autour de l'origine
du repère de modélisation associé à la fonction.
Quelle(s) transformation(s) géométrique(s) de modification du repère courant (placée(s) entre la configuration
de projection de la caméra et la modélisation effective) doit on réaliser pour que cette scène soit vue centrée
dans la fenêtre de visualisation comme placée devant la caméra à une distance de 100.0 avec un axe de projection
selon la direction (0.0, 0.0, -1.0) dans le repère de modélisation de la scène?
A quelle position de placement de la caméra cela correspond-t-il dans le repère de modélisation de la scène?
b) On considère la scène de la question (a).
Quelle(s) transformation(s) géométrique(s) de modification du repère courant (placée(s) entre la configuration
de projection de la caméra et la modélisation effective) doit on réaliser pour que cette scène soit vue centrée
dans la fenêtre de visualisation comme placée devant la caméra à une distance de 100.0 avec un axe de visualisation
selon la direction (-1.0, 0.0, -1.0) dans le repère de modélisation?
A quelle position de placement de la caméra cela correspond-t-il dans le repère de modélisation de la scène?
c) On considère la scène de la question (a).
Quelle(s) transformation(s) géométrique(s) de modification du repère courant (placée(s) entre la configuration
de projection de la caméra et la modélisation effective) doit on réaliser pour que cette scène soit vue centrée
dans la fenêtre de visualisation comme placée devant la caméra à une distance de 100.0 avec un axe de visualisation
selon la direction (-1.0, -1.0, -1.0) dans le repère de modélisation?
A quelle position de placement de la caméra cela correspond-t-il dans le repère de modélisation de la scène?
Solutions
![]()
TP n°1 : Premières implantations OpenGL
Exercice n°1
Télécharger le fichier archive 2012-2013.zip. Ce fichier archive contient une
"solution" Visual Studio 2010.
Après extraction, un répertoire IG-2012-2013 est créé qui contient lui-même 5 répertoires:
- Bin pour les exécutables,
- Include pour les fichiers d'entête OpenGL (fichiers non présents dans Visual Studio),
- Lib pour les fichiers librairie OpenGL (fichiers non présents dans Visual Studio),
- Projet pour le fichier de description de la solution (Projet.sln) et les répertoires contenant les projets
faisant partie de la solution (Un seul répertoire actuellement: Exemple),
- Src pour les fichiers source des projets inclus dans la solution.
La solution comprend un seul projet nommé Exemple. Ce projet inclut un seul fichier source Exemple.cpp et est
configuré pour une compilation utilisant OpenGL:
- fichiers d'entête (répertoire implicite ../../Include),
- fichiers librairie (fichiers OpenGL32.ms.lib, glu32.ms.lib, glut32.ms.lib),
- copie de l'exécutable dans le répertoire Bin.
La compilation (génération) de ce projet doit conduire à la création d'un exécutable nommé Exemple.exe dans
le répertoire Bin. Son exécution requière les dll OpenGL32.lib et Glu32.lib (toujours présentes dans le système
d'exploitation Windows) ainsi que la librairie Glut32.lib (jamais présente dans le système d'exploitation
Windows mais dont il existe une copie dans le répertoire Bin).
Extraire l'archive IG-2012-2013. Lancer Visual Studio 2010 et charger la solution. Vérifier la compilation et l'exécution du projet Exemple.
![]()
TP n°2 : Scènes OpenGL et caméras
Exercice n°1
Implanter et tester le fonctionnement de l'exercice n°1 du TD n°1 (quatre cubes).
- Créer une copie du fichier source Exemple.cpp.
- Supprimer la ligne glutIdleFunc de la fonction main.
- Modifier la fonction keyboard pour que l'animation soit considérée comme inactivée au lancement mais reste activable (animation d'une scène immobile! -> Réaffichage en boucle de la même image).
- Réécrire la fonction void scene(void) avec celle du TD. On utilisera la fonction void glutSolidCube(double c) de la librairie GLUt comme fonction de modélisation de cube.
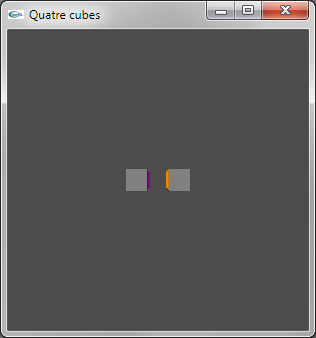
Conseil: Créer un nouveau projet au sein de la solution pour chaque nouveau fichier source testé au cours d'une séance de TP.
Exercice n°2
Tester les deux possibilités existant pour ajuster la taille des objets à l'écran de manière à voir la scène en gros plan:
- Jouer sur l'angle d'ouverture de la caméra virtuelle.
- Jouer sur la distance entre la scène et la caméra virtuelle.

Exercice n°3
a) Ajouter un contrôle clavier pour que les cubes de la scène puissent être remplacés par des sphères (et réciproque). La fonction void glutSolidSphere(double rayon, int n,int m) peut être utilisée pour modéliser une sphère.
b) Ajouter un contrôle clavier pour que les objets puissent être affichés soit en mode plein, soit en mode fil de fer (fonction glPolygonMode d'OpenGL).
c) Adapter l'animation de la scène de manière que la scène tourne sur elle-même.
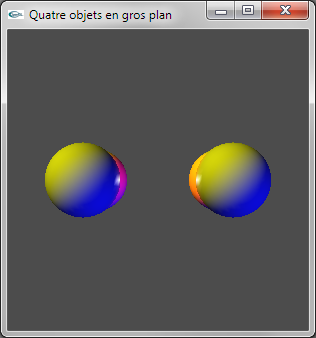
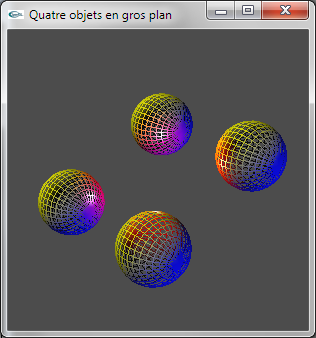
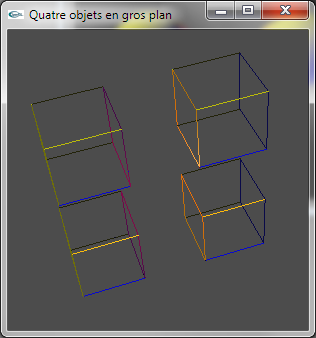
Exercice n°4
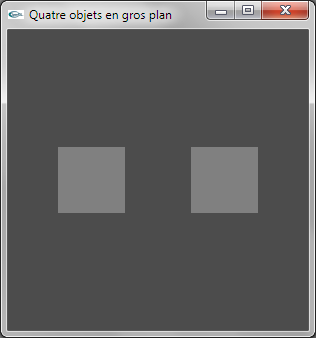
Modifier la caméra de manière que la projection de visualisation soit modifiée en une projection parallèle orthographique avec la scène en gros plan.
Exercice n°5
a) Vérifier le bon paramétrage des deux caméras pour que le ratio largeur/hauteur de la caméra virtuelle corresponde bien au ratio du viewport (pas de déformation de l'affichage).
b) S'assurer que la scène reste bien entièrement visible que le ratio de viewport d'affichage soit plus grand ou plus petit que 1.0.

Solutions
![]()
TD n°4 : Lumières et matériaux en OpenGL
Exercice n°1
a) Développer le code source OpenGL permettant de configuer la lumière n°0 en tant que lumière ponctuelle placée en position (0.0, 0.0, 2.5). Sa composante d'émission diffuse sera rouge. Sa composante d'émission spéculaire sera blanche.

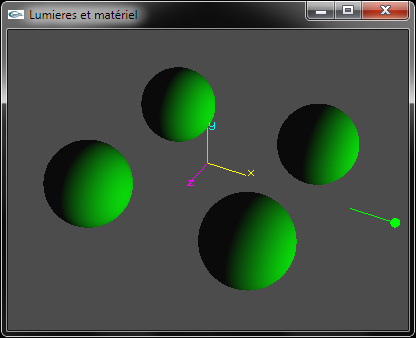
b) Développer le code source OpenGL permettant de configuer la lumière n°1 en tant que lumière directionnelle de direction d'incidence (1.0, 0.0, 0.0). Sa composante d'émission diffuse sera verte. Sa composante d'émission spéculaire sera blanche.
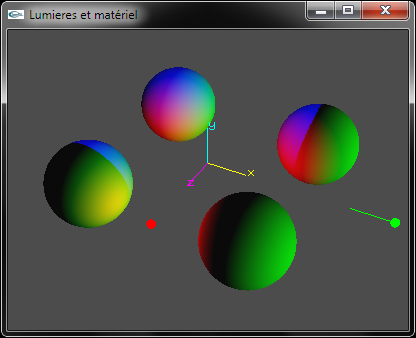
c) Développer le code source OpenGL permettant de configuer la lumière n°2 en tant que spot placé en position (2.0, 10.0, 2.0), orienté vers le point de coordonnées (-2.0, 0.0, -2.0) et d'ouverture 20.0°. Sa composante d'émission diffuse sera bleue. Sa composante d'émission spéculaire sera blanche.

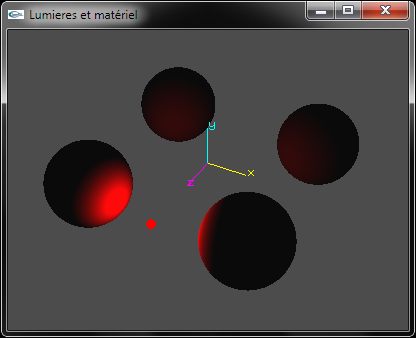
d) Ajouter au code de paramétrage la lumière 0 les appels OpenGL permettant de configurer une atténuation de l'éclairage en fonction inversement proportionnelle du carré de la distance entre la source lumineuse et le point éclairé.

e) Proposer une solution permettant de choisir la position de placement de la lumière ponctuelle de la question (a) et la direction d'orientation de la lumière directionnelle de la question (b) par rotation d'une valeur d'angle autour de l'axe Oy.

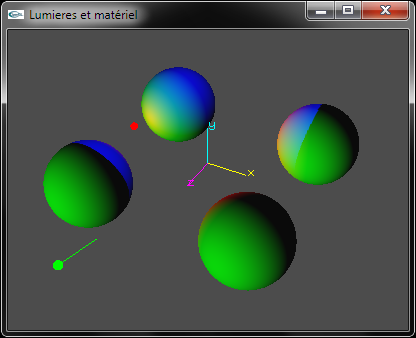
Exercice n°2
a) Développer le code source OpenGL permettant de configurer le matériel pour qu'il adopte la couleur blanche en diffusion et la couleur noire en spéculaire, ambiant et émission.
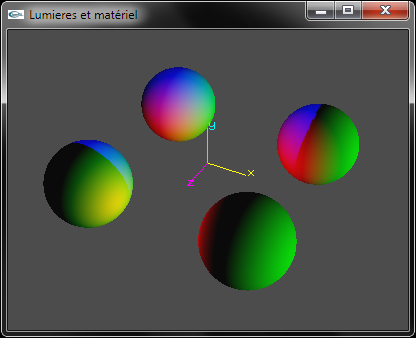

b) Développer le code source OpenGL permettant de configurer le matériel pour qu'il adopte la couleur rouge en diffusion et la couleur noire en spéculaire, ambiant et émission.
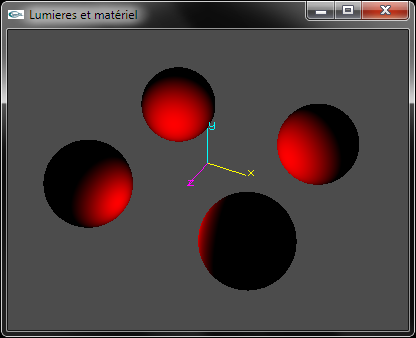
c) Développer le code source OpenGL permettant de configurer le matériel pour qu'il adopte la couleur jaune en diffusion et la couleur noire en spéculaire, ambiant et émission.
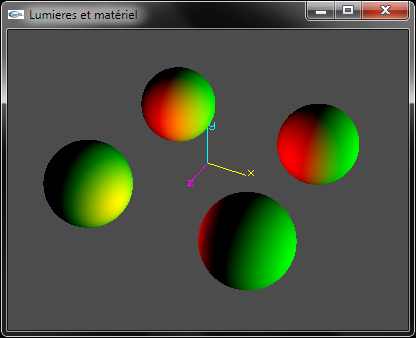
d) Développer le code source OpenGL permettant de configurer le matériel pour qu'il adopte la couleur blanche en diffusion et spéculaire et la couleur noire en ambiant et émission. La réflectivité est configurée avec la valeur 64.0.

Solution
|
GLUT |
||
| Lumières et matériel | ||
![]()
TP n°3 : Lumières et matériaux en OpenGL
Implanter les exercice du TD n°4 sur la scène du TP n°2 constituée de 4 sphères.
Solution
|
GLUT |
||
| Lumières et matériel | ||
![]()
TD n°5 : Mathématiques de l'Informatique Graphique
Exercice n°1
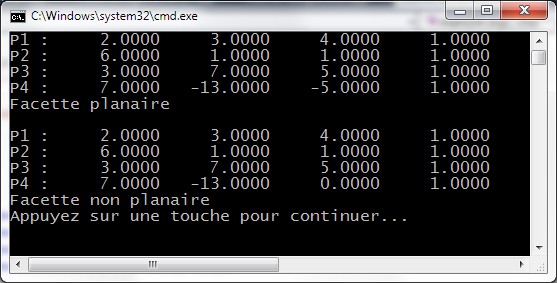
Proposer une méthode permettant de tester la planarité d'une facette à 4 sommets.
Exercice n°2
a) Développer en C++ une classe CoordonneesHomogenes3D.
b) Dériver de la classe CoordonneesHomogenes3D une classe Position3D pour le stockage de positions dans un espace à trois dimensions.
c) Dériver de la classe CoordonneesHomogenes3D une classe Direction3D pour le stockage de directions dans un espace à trois dimensions.
d) Développer une méthode de calcul du produit scalaire de deux Direction3D.
e) Développer une méthode de calcul du produit vectoriel de deux Direction3D.
f) Implanter une fonction ou une méthode de test de la planarité de facettes à 4 sommets.
Exercice n°3
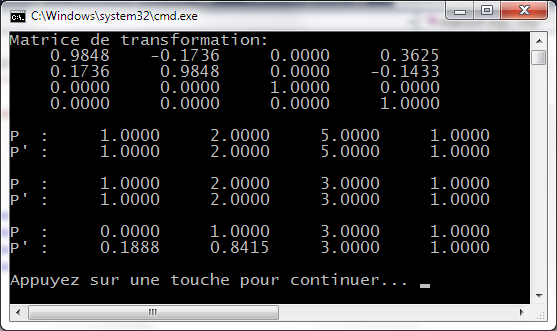
a) Développer en C++ une classe TransformationGeometrique3D en coordonnées homogènes.
b) Dériver de la classe TransformationGeometrique3D une classe Position3D pour le stockage d'opérateurs de type translation de vecteur (tx, ty, tz).
c) Dériver de la classe TransformationGeometrique3D une classe Rotation3D pour le stockage d'opérateurs de type rotation d'angle a autour de l'axe (ax, ay, az) passant par l'origine.
d) Implanter une méthode de transformation d'une position ou d'une direction par une translation ou une rotation.
e) Implanter une méthode de composition d'une transformation géométrique par une transformation géométrique.
Solutions
![]()
TP n°4 : Mathématiques de l'Informatique Graphique
Implanter l'exercice n°2 du TD n°5

Solution
![]()
TP n°5 : Mathématiques de l'Informatique Graphique
Implanter l'exercice n°3 du TD n°5.
![]()
TD n°6 : Outils algorithmiques de l'Informatique Graphique
Implanter une fonction de remplissage 2D d'un triangle.
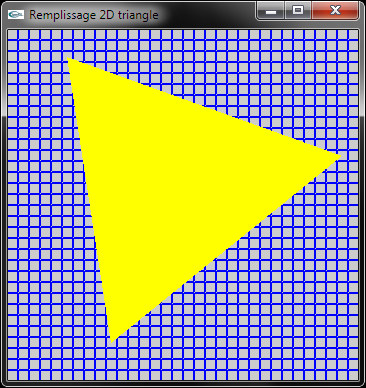
Méthode: Remplir un triangle en 2D peut être réalisé en traçant toutes les lignes horizontales de pixels délimitées par ses bords gauche et droit. Il convient donc de déterminer les abscisses extrèmes de ces lignes horizontales pour chacun des y compris entre ymin et ymax où ymin (resp. ymax) est la valeur minimale (resp. maximale) des ordonnées des 3 sommets de définition du rectangle.
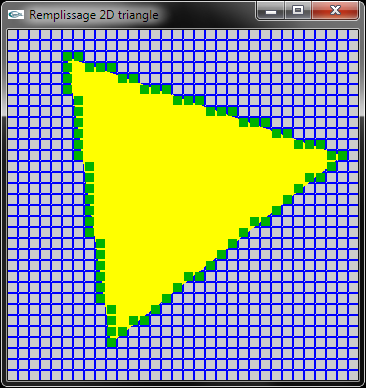
Ainsi, deux tableaux x1 et x2 sont calculés dont l'indice correspond à l'ordonnée d'une ligne de
pixels.
Le calcul de ces deux tableaux est réalisé par implantation et adaptation de l'algorithme de Bresenham pour
le tracé de segments de droite. Cet algorithme adapté est appliqué aux trois bords du triangle rempli.


Solutions
![]()
TP n°6 : Gestion de la souris en GLUT+OpenGL et algorithmique de l'Informatique Graphique
Exercice n°1
Comme tous les autres modes d'interactions avec l'utilisateur, la gestion de la souris est à programmer sous forme événementielle. Les trois fonctions glutMouseFunc, glutMotionFunc et glutPassivMotionFunc permettent l'exécution de fonctions en réaction aux événements souris.
- glutMouseFunc: L'utilisateur utilise les boutons de la souris sur la fenêtre d'affichage.
- glutMotionFunc: L'utilisateur déplace la souris sur la fenêtre d'affichage avec un (ou plusieurs) bouton appuyé.
- glutPassiveMotionFunc: L'utilisateur déplace la souris sur la fenêtre d'affichage sans bouton appuyé.
On trouvera dans le fichier glut-3_spec.pdf les spécifications de GLUT en version 3 avec une description précise de ces trois fonctions.
a) Tester l'utilisation de la souris en développant un programme affichant une fenêtre vide mais permettant à l'utilisateur d'obtenir par affichage texte dans la console les coordonnées des clics de souris (bouton gauche) qu'il réalise.


b) Faire évoluer le programme précédent de manière que, lorsque l'utilisateur clique, un marqueur circulaire de 10 pixels de rayon apparaisse là où il a cliqué. 2 marqueurs sont gérés. Chaque nouveau clic de souris à pour conséquence la modification de la position de l'avant dernier marqueur déplacé.
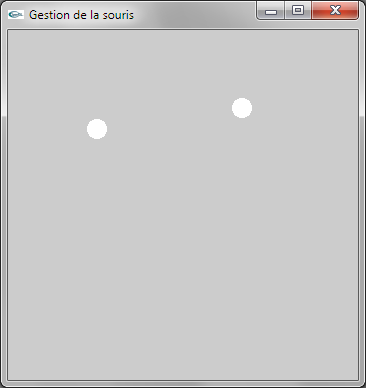

c) Faire évoluer le programme précédent de manière que les deux marqueurs soient reliés par un segment de droite.
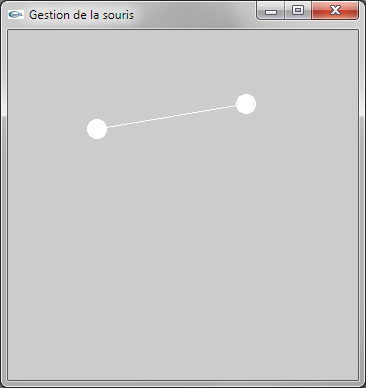
d) Faire évoluer le programme précédent de manière que si l'utilisateur maintient enfoncé le bouton gauche de la souris, la scène soit réaffichée dynamiquement en fonction de la position de la souris.
Exercice n°2
Faire évoluer le programme de la question (d) de l'exercice n°1 de manière qu'un clic du bouton droit
de la souris entraîne l'affichage dans la console des coordonnées de tous les pixels allumés lors du tracé
du segment de droite.
Il conviendra d'implanter l'algorithme de Bresenham pour le tracé de segments non pas dans une version
affichant réellement des pixels, mais en substituant à cet affichage graphique un affichage texte dans la console.

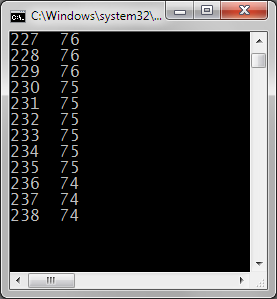
Solutions
|
GLUT |
||
| Gestion de la souris | ||
![]()
TP n°7 : Plaçage de texture bitmap en OpenGL
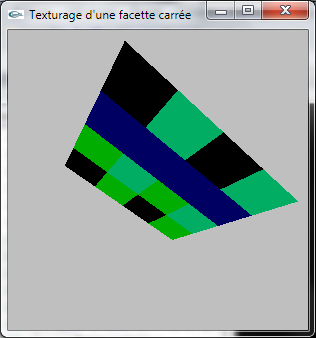
Le programme Texturage.cpp modélise une facette carrée recouverte d'une texture bitmap chargée depuis le fichier Image.raw (format raw).
Remarque: Ce code source montre comment utiliser les touches de curseur.
a) Télécharger, compiler et exécuter ce programme pour vérifier son bon fonctionnement.
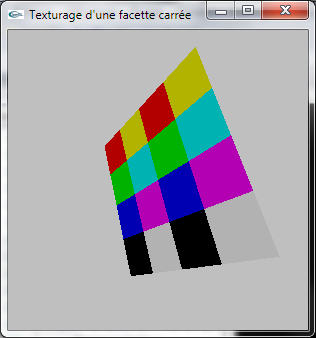
b) La fonction suivante est la fonction de modélisation de cube développée au TD n°2:
static void solidCube(double ct) {
float c =(float) ct/2.0F;
glBegin(GL_QUADS);
{ glNormal3f(0.0F,0.0F,-1.0F);
glVertex3f( c, c,-c);
glVertex3f( c,-c,-c);
glVertex3f(-c,-c,-c);
glVertex3f(-c, c,-c); }
{ glNormal3f(0.0F,0.0F,1.0F);
glVertex3f( c, c, c);
glVertex3f(-c, c, c);
glVertex3f(-c,-c, c);
glVertex3f( c,-c, c); }
{ glNormal3f(-1.0F,0.0F,0.0F);
glVertex3f(-c, c,-c);
glVertex3f(-c,-c,-c);
glVertex3f(-c,-c, c);
glVertex3f(-c, c, c); }
{ glNormal3f(1.0F,0.0F,0.0F);
glVertex3f( c, c, c);
glVertex3f( c,-c, c);
glVertex3f( c,-c,-c);
glVertex3f( c, c,-c); }
{ glNormal3f(0.0F,-1.0F,0.0F);
glVertex3f(-c,-c, c);
glVertex3f(-c,-c,-c);
glVertex3f( c,-c,-c);
glVertex3f( c,-c, c); }
{ glNormal3f(0.0F,1.0F,0.0F);
glVertex3f( c, c, c);
glVertex3f( c, c,-c);
glVertex3f(-c, c,-c);
glVertex3f(-c, c, c); }
glEnd();
}
Adapter cette fonction pour qu'elle supporte le plaçage de texture.

Texturage 2D avec le fichier Image.raw

Texturage 2D avec le fichier Damier.raw
c) La fonction suivante est la fonction de modélisation de cylindre développée au TD n°2:
#ifndef M_PI
#define M_PI 3.14159
#endif
static void solidCylindre(double hauteur,double rayon,int ns) {
float h = hauteur/2;
glBegin(GL_QUAD_STRIP);
for( int i = 0 ; i <= ns ; i++ ) {
float a = (2*M_PI*i)/ns;
float cs = cos(a);
float sn = -sin(a);
glNormal3f(cs,0.0F,sn);
float x = rayon*cs;
float z = rayon*sn;
glVertex3f(x,h,z);
glVertex3f(x,-h,z); }
glEnd();
glBegin(GL_POLYGON);
glNormal3f(0.0F,1.0F,0.0F);
for( int i = 0 ; i < ns ; i++ ) {
float a = (2*M_PI*i)/ns;
float cs = cos(a);
float sn = -sin(a);
float x = rayon*cs;
float z = rayon*sn;
glVertex3f(x,hauteur/2.0F,z); }
glEnd();
glBegin(GL_POLYGON);
glNormal3f(0.0F,-1.0F,0.0F);
for( int i = 0 ; i < ns ; i++ ) {
float a = (2*M_PI*i)/ns;
float cs = cos(a);
float sn = sin(a);
float x = rayon*cs;
float z = rayon*sn;
glVertex3f(x,-hauteur/2.0F,z); }
glEnd();
}
Adapter cette fonction pour qu'elle supporte le plaçage de texture.
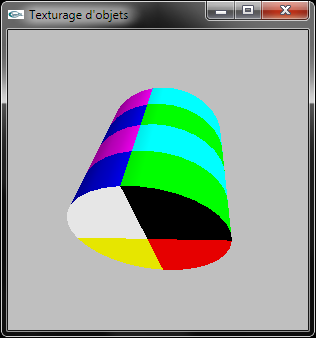

Solutions
![]()
TD n°7 : Clipping de Cohen-Sutherland
On considère les classes suivantes:
|
class Position2D; |
|
class Segment2D { |
| class Rectangle2D { public : Position2D *ig; Position2D *sd; public : /* Constructeurs */ Rectangle2D(void); Rectangle2D(Position2D *p1,Position2D *p2); Rectangle2D(Rectangle2D *c); /* Destructeur */ ~Rectangle2D(void); }; |
a) Développer une méthode permettant de déterminer le code de Cohen-Sutherland (entier) d'une Position2D vis à vis d'un Rectangle2D.
b) Développer une méthode permettant de déterminer l'abscisse de l'intersection entre un Segment2D et une droite horizontale (connue par son ordonnée).
c) Développer une méthode permettant de déterminer l'ordonnée de l'intersection entre un Segment2D et une droite verticale (connue par son abscisse).
d) Développer une méthode permettant de clipper un Segment2D dans un Rectangle2D (algorithme de Cohen-Sutherland).
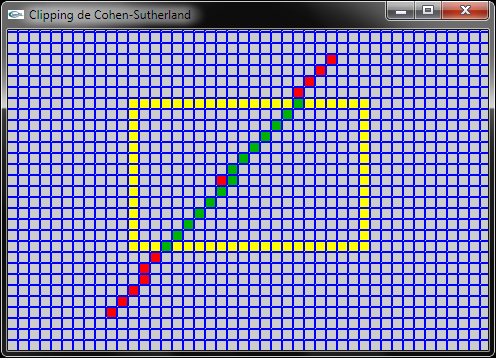
Solutions
![]()
TP n°8 : Calcul des directions de réflexion et transmission pour le lancer de rayons
On considère les classes Position3D et Direction3D définies au cours des TD-TP précédents:
- Position3D.h
- Position3D.cpp
- Direction3D.h
- Direction3D.cpp
- CoordonneesHomogenes3D.h
- CoordonneesHomogenes3D.cpp
a) Concevoir une classe permettant de modéliser un objet de type rayon lumineux utilisé au sein d'un programme de rendu par lancer de rayons.s.
b) Concevoir une méthode de la classe Direction3D permettant de calculer la direction d'un rayon réfléchi lors d'une réflexion spéculaire.
c) Concevoir une méthode de la classe Direction3D permettant de calculer la direction d'un rayon transmis à l'interface entre deux milieux lors du passage entre ces deux milieux.
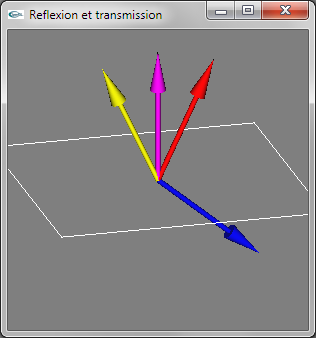
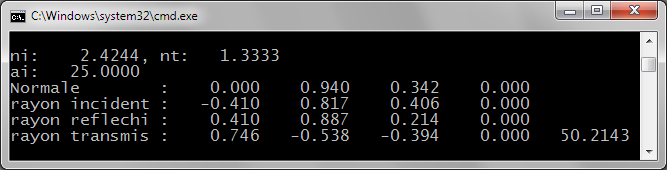
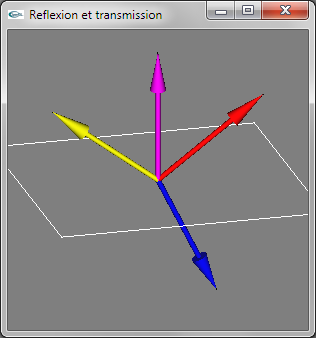
Rayon incident en jaune, normale en magenta, rayon réfléchi en rouge, rayon transmis en bleu (dévié vers le plan d'interface)
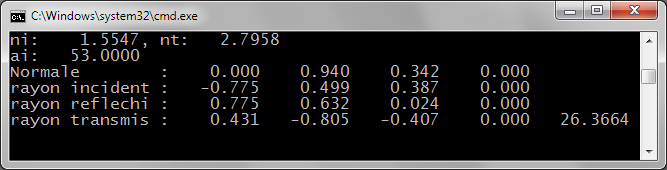
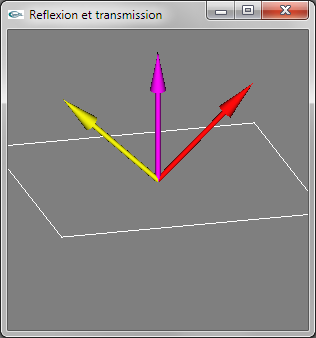
Rayon transmis dévié vers le vecteur opposé au vecteur normal
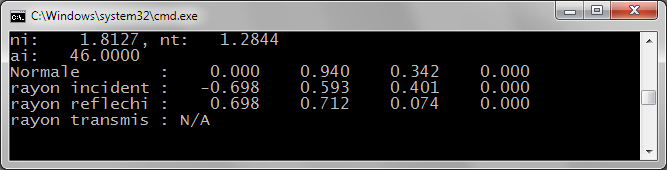
Pas de rayon transmis
On pourra utiliser le programme ReflexionEtTransmission.cpp
pour tester les deux méthodes développées.
Ce programme utilise les composants complémentaires suivants:
- La librairire Modules-2012-2013.lib associée
au fichier d'entête ModuleFleche.h
- Les classes TransformationGeometrique3D et Rotation3D (développées au cours de TD/TP précédents):
- TransformationGeometrique3D.h
- TransformationGeometrique3D.cpp
- Rotation3D.h
- Rotation3D.cpp
Ce programme ouvre une fenêtre dans laquelle sont affichés un rayon incident, une interface, la normale à cette
interface ainsi que les rayons réfléchi et transmis calculés au moyen des méthodes implantées.
Solutions
![]()
TP n°9 : Calcul de la quantité d'énergie diffusée en un point éclairé par une source lumineuse ponctuelle
On considère les classes Rvb, Couleur, Energie, Lumiere et LumiereDirectionnelle suivantes:
- Rvb.h
- Rvb.cpp
- Couleur.h
- Couleur.cpp
- Energie.h
- Energie.cpp
- Lumiere.h
- Lumiere.cpp
- LumiereDirectionnelle.h
- LumiereDirectionnelle.cpp
| class Rvb { public : double r; double v; double b; public : /* Constructeurs */ Rvb(void); Rvb(double r,double v,double b); Rvb(float r,float v,float b); Rvb(double *c); Rvb(float *c); Rvb(Rvb *c); /* Destructeur */ ~Rvb(void); }; |
|
class Couleur:public Rvb { |
| class Energie:public Rvb { public : /* Constructeurs */ Energie(void); Energie(double r,double v,double b); Energie(float r,float v,float b); Energie(double *c); Energie(float *c); Energie(Energie *c); /* Destructeur */ ~Energie(void); }; |
| class Lumiere { public : Couleur *c; double intensite; bool on; public : /* Constructeurs */ Lumiere(void); Lumiere(Lumiere *c); /* Destructeur */ ~Lumiere(void); }; |
|
|
| class LumiereDirectionnelle:public Lumiere { public : Direction3D *d; public : /* Constructeurs */ LumiereDirectionnelle(void); LumiereDirectionnelle(LumiereDirectionnelle *ld); /* Destructeur */ ~LumiereDirectionnelle(void); }; |
a) Développer une méthode permettant de calculer la quantité d'énergie diffusée sous l'éclairage d'une LumiereDirectionnelle en une Position3D extraite d'une surface où la normale est connue sous la forme d'une Direction3D. Les coefficients de diffusion de la surface sont définis par la donnée d'une Couleur.



Sphère éclairée par une lumière ponctuelle
en pur OpenGL à gauche, en utilisant le calcul de diffusion "maison"
On considère la classe LumierePonctuelle suivante:
- LumierePonctuelle.h
- LumierePonctuelle.cpp
| class Position3D; |
|
class LumierePonctuelle:public Lumiere { |
b) Développer une méthode permettant de calculer la quantité d'énergie diffusée sous l'éclairage d'une LumierePonctuelle en une Position3D extraite d'une surface où la normale est connue sous la forme d'une Direction3D. Les coefficients de diffusion de la surface sont définis par la donnée d'une Couleur.
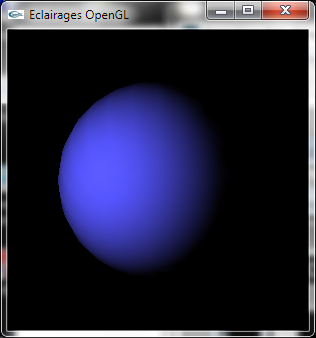


Sphère éclairée par une lumière directionnelle
en pur OpenGL à gauche, en utilisant le calcul de diffusion "maison"
On pourra utiliser le programme DiffusionsLambertiennes.cpp
pour tester les deux méthodes développées.
Ce programme affiche deux fenêtres avec, dans la première, une sphère éclairée au moyen de l'implantation
OpenGL du calcul de diffusion de Lambert et dans la seconde, une sphère éclairée au moyen de l'implantation
réalisée.
Remarque: Ce code source montre comment utiliser deux (plusieurs par extension) fenêtres ainsi que les menus popup.
Solutions
![]()
TD n°8 : Calcul d'une courbe de Bézier
On considère la classe LignePolygonale3D suivante:
| class Position3D; |
|
class LignePolygonale3D { |
Cette classe permet le stockage d'un ensemble ordonné de Position3D.
Développer un nouveau constructeur pour cette classe permettant de créer la courbe de Bézier définie sur n sommets à partir d'une LignePolygonale3D.


Solutions
|
GLUT |
||
| Une courbe de Bézier | ||
![]()
TP n°10 : Implantation du calcul d'une courbe de Bézier
Implanter le TD n°8.
Associées au le programme Bezier2.cpp les classes
LignePolygonale3D.h et LignePolygonale3D.cpp
pourront être utilisées comme base (à compléter) pour tester le constructeur développé.
Ce programme affiche une fenêtre avec une ligne polygonale en jaune et la courbe de Bézier générée à partir de
cette ligne polygonale.
Attention: Ce code source est spécifique à Microsoft Visual Studio car il comporte des instructions permettant
de vérifier que les allocations/désallocations dynamiques de mémoire réalisées par new, malloc, calloc, realloc
pour les allocations, delete et free pour les désallocations sont correctement réalisées.
-> Tout ce qui est
alloué et bien désalloué à la sortie du programme.
A noter: Cette vérification n'est réalisable qu'en
mode de compilation et d'exécution "Debug".
Solutions
|
GLUT |
||
| Une courbe de Bézier | ||
![]()