Sujets et Corrections
de TD et TP
TD n°1
Création de scènes
en VRML 1.0
TD n°2
Création de scènes
OpenGL
TD n°3
Les primitives
graphiques
en OpenGL
TD n°4
Programmation
d'animations
en OpenGL
TD n°5:
Matériaux
et lumières
en VRML
TD n°6:
Quelques bases
mathématiques
de l'infographie
TD n°7:
Le plaçage
de texture en VRML
et en OpenGL
TD n°8:
Le remplissage
de cercles
et de triangles 2D
TD n°9:
Programmation
de classes
de gestion
des coordonnées
homogènes
TP n°1
Prise en mains
d'un environnement
de programmation
VRML
TP n°2
Prise en mains
d'un environnement
de programmation
OpenGL
TP n°4:
Gestion
des caméras
en OpenGL
TP n°5:
Les matériaux
et les lumières
en OpenGL
TP n°6:
Mathématiques
pour les calculs
d'éclairage
TP n°7:
Le clipping
par l'algorithme
de Cohen-Sutherland
Dernière modification
16/11/09 07:03:35
TD n°1: Création de scènes VRML 1.0
Exercice n°1
(1) Programmer en VRML la scène suivante sans utiliser le nœud Separator ailleurs que pour le Separator d'encadrement global du fichier:
Quatre cubes de coté de longueur 1.0 aux positions (2.0,0.0,2.0), (2.0,0.0,-2.0), (-2.0,0.0,2.0) et (-2.0,0.0,-2.0).
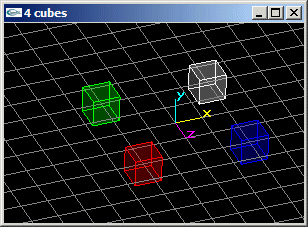
(2) Reprogrammer en VRML la scène précédante en utilisant le nœud Separator pour rendre les objets indépendants les uns des autres.
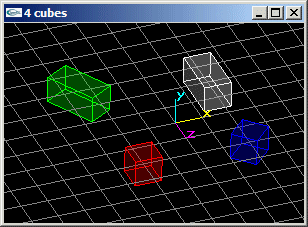
(3) Reprogrammer en VRML la scène précédante en apportant les modifications suivantes:
- Le cube en position (2.0,0.0,2.0) subit une rotation de 45° autour de l'axe y passant par son centre.
- Le cube en position (2.0,0.0,-2.0) subit un zoom de rapport (1.0,1.0,2.0) par rapport à son centre.
Le cube en position (-2.0,0.0,-2.0) n'est plus centré en ce point. Il est placé de telle manière qu'il présente une rotation de 30° autour de l'axe y passant par le sommet (-2.0,0.0,-2.0) et que ce sommet soit le centre de sa base inférieure. En outre, il subit un zoom de rapport (1.0,1.0,2.0) par rapport à son centre.
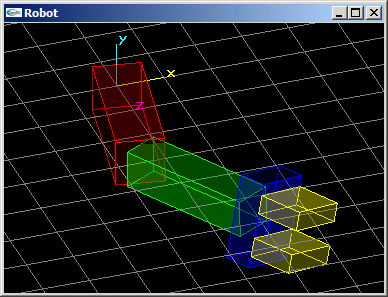
Exercice n°2
Programmer la scène modélisant un bras robot composé d'un avant-bras,
d'un bras, et d'une paire de pinces.
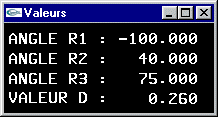
L'avant-bras est articulé pour tourner autour de l'axe y d'un angle r1. Il s'agit d'un
parallélépipède rectangle de dimension (3.0,1.0,1.0) (rouge). Le bras est articulé
autour de l'axe y au bout de l'avant bras pour un angle r2. Il s'agit d'un
parallélépipède rectangle de dimension (3.0,0.8,0.8) (vert). La pince est située au
bout du bras. Elle peut tourner autour de l'axe du bras pour un angle r3. L'embase de la
paire de pinces est un parallélépipède rectangle de dimension (0.6,1.2,1.8) (bleu).
Chacune des mâchoires est un parallélépipède rectangle de dimension (1.0,1.2,0.4)
(jaune) à même de se déplacer longitudinalement d'une valeur d pour réaliser une
ouverture totale de 2xd.
TD n°2: Création de scènes OpenGL
Exercice n°1
Soit la scène composée de n cubes de cotés 1 centrés sur les sommets d'un polygone régulier de rayon 3 lui-même centré sur O et plongé dans le plan xOy. Les cubes doivent présenter une face directement orientée vers O.

Réaliser l'implantation OpenGL de cette scène.
Exercice n°2
Soit la scène composée de huit cubes de cotés 1 centrés sur les
sommets d'un cube de rayon 4 lui-même centré sur O, et de 12 cylindres de rayon 0.25 et
de longueur 3.0 joignant ces 8 sommets entre eux pour matérialiser les arêtes du cube de
coté 4.
Implanter cette scène.

Fichiers sources pour dessiner des cylindres
ModuleCylindres.cpp
ModuleCylindres.h
TD n°3: Les primitives graphiques en OpenGL
Exercice 1
a) Ecrire une fonction de modélisation d'une boite cubique de dimension c centrée sur l'origine du repère. Cette fonction devra seulement assurer la création des facettes (cubes rouges sur l'image proposée).
b) Modifier la fonction précédente pour y inclure la gestion des normales aux facettes (utilisées pour les calculs d'éclairages) (cubes bleu et vert sur l'image proposée).
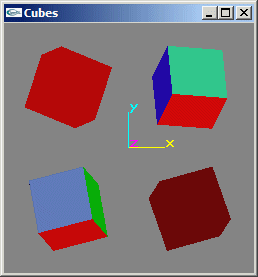
Exercice 2
a) Ecrire une fonction de modélisation d'un cylindre de rayon r, de hauteur h, possédant n sections radiales, centré sur l'origine et d'axe y. Cette fonction devra seulement assurer la création des facettes (cylindres bruns sur l'image proposée).
b) Modifier la fonction précédente pour y inclure la gestion des normales aux facettes (utilisées pour les calculs d'éclairages) (cylindres avec dégradé sur l'image proposée).

TD n°4: Programmation d'animations
Exercice 1
a) Programmer l'animation d'une sphère de rayon 1 selon une trajectoire circulaire de rayon 3 centrée sur l'origine du repère et définie dans le plan xOy. Cette animation est réalisée à raison de 0.5° de rotation entre chaque image.

b) Modifier le programme précédent de telle manière que la sphère réalise un mouvement de va et vient cyclique de façon que revenue à sa position de départ, elle reparte en marche arrière.
c) Modifier le programme précédent de telle manière que la touche Enter du clavier soit utilisable pour activer/désactiver l'animation. En cas de réactivation, l'animation repart là où elle avait été interrompue.
Exercice 2
Programmer un mouvement hélicoïdal. Les paramètres sont les suivants:
- L'objet en mouvement est une sphère de rayon 1.
- L'axe du mouvement hélicoïdal est l'axe -Oy.
- Le rayon du mouvement est 3.
- Le point de départ de la sphère est (0.0F,5.0F,-3.0F).
- La perte d'"altitude" (déplacement selon l'axe y) entre chaque tour est 2.
- Le nombre de tours est 5.
- La sphère effectue une rotation de 1° entre chaque image.
- Une fois arrivée à son point d'arrivée, la sphère remonte à son point de départ selon une trajectoire linéaire uniforme effectuée en 1000 images.
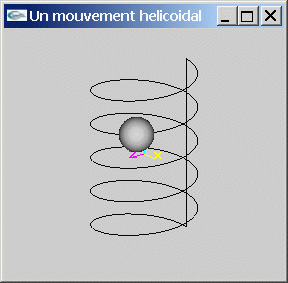

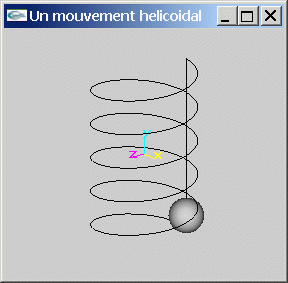
Exercice 3
Programmer une animation où deux sphères de rayon 1, suspendues à deux cylindres de
longueur 10 et de rayon 0.25 matérialisant des fils, s'entrechoquent l'une l'autre de
manière cyclique.
Pour s'implifier la programmation, les mouvements de va et vient seront effectués à la
vitesse radiale constante de 1° entre chaque image (pas de mouvement balistique). Les
sphères remontent jusqu'à l'horizontale au bout de leurs cylindres respectifs.
Exercice 4
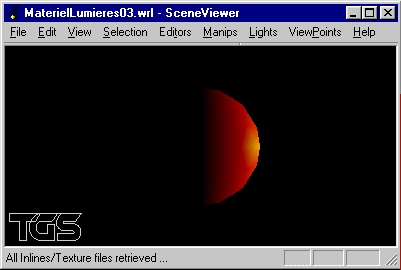
On souhaite programmer une scène animée en OpenGL. Cette scène représente, avec élimination des parties cachées, une sphère de rayon 1, de position initiale (0.0,10.0,0.0) tombant balistiquement selon l'axe -Oy pour rebondir centrée au point (0.0,0.0,0.0), revenir se placer en position initiale et s'immobiliser.
- L'animation est déclenchée par l'appuie de la touche 'A' du clavier.
- L'animation est composée de 1001 images successives numérotées de 0 à 1000 (numéros 0 à 499 à l'allée, 500 au point de rebond, 501 à 1000 au retour)
- La coordonnée y en phase descendante est obtenue par la formule
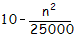 où n désigne le numéro de l'image. La
coordonnée y en phase montante est
où n désigne le numéro de l'image. La
coordonnée y en phase montante est 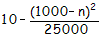 .
.
- Ecrire la fonction init.
- Ecrire la fonction idle.
- Ecrire la fonction key.
- Ecrire la fonction display.
GLUt |
||
| La trajectoire circulaire (a) | ||
| La trajectoire circulaire (b) | ||
| La trajectoire circulaire (c) | ||
| La trajectoire hélicoïdale | ||
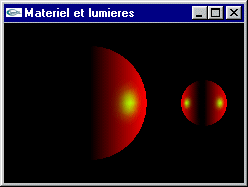
TD n°5: Les lumières et matériaux en VRML
Gestion en VRML des matériaux et des lumières
Exercice 1
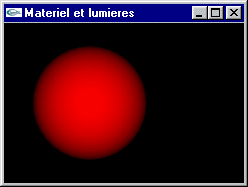
a) Ecrire une scène composée d'une sphère de rayon 5 centrée sur l'origine du repère et affectée d'un matériel avec uniquement de la diffusion dans le rouge.
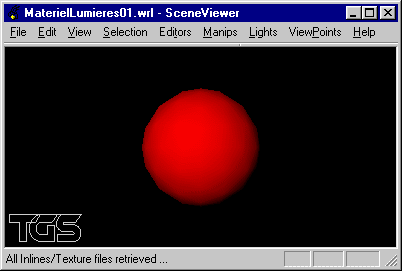
b) Modifier la scène précédente pour que le matériel intègre une réflexion spéculaire dans le vert.
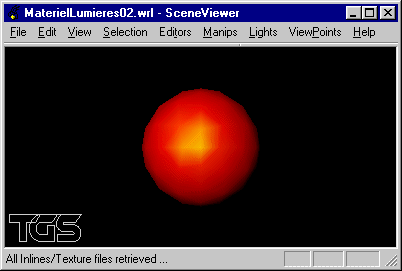
c) Modifier la scène précédente pour y intégrer un éclairage sous la forme d'une source lumineuse directionnelle blanche éclairant depuis la droite.
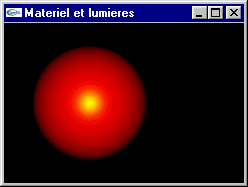
d) Modifier la scène précédente pour y inclure une seconde sphère de rayon 2 placée en position (10, 0, 0) possédant le même matériel que la première ainsi qu'une seconde source lumineuse ponctuelle blanche placée à l'origine.

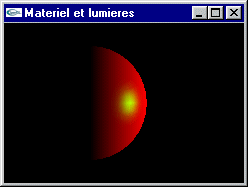
e) Modifier la scène précédente pour y inclure une source lumineuse spot placée en position (0, 0, 10) orientée vers l'origine et éclairant partiellement la grosse sphère.
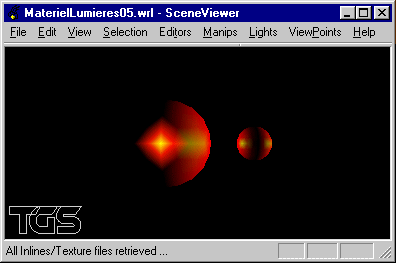
Solutions
VRML |
||||||
| Les fichiers VRML | ||||||
Exercice 2
Soient deux sphères de rayon 1, placées en position (5, 0, 0) et (-5, 0, 0) et blanches en diffusion. Soient deux sources lumineuses ponctuelles placées à l'origine du repère et émettant dans le vert et dans le bleu. Construire la scène de telle manière que la sphère de droite soit éclairée uniquement par la lumière verte, et la sphère de gauche uniquement par la lumière bleue.
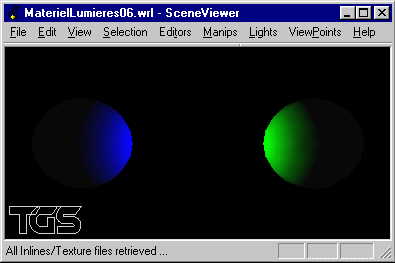
Modifier le matériau des deux sphères pour les rendre transparentes.
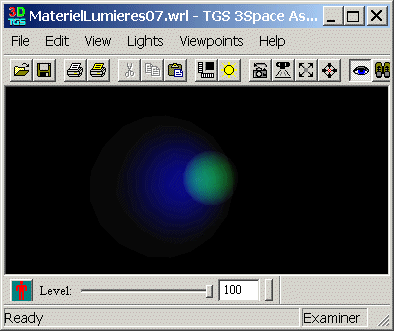
Solution
VRML |
||
| Le fichier VRML | ||
TD n°6: Quelques bases mathématiques de l'infographie
1) Définir une structure de données permettant de stocker une position dans un espace à 3 dimensions.
2) Définir une structure de données permettant de stocker une direction dans un espace à 3 dimensions.
3) Ecrire une fonction de calcul de la direction définie entre deux positions.
4) Ecrire une fonction calculant la norme d'une direction.
5) Ecrire une fonction de normalisation d'une direction.


6) Ecrire une fonction calculant le produit scalaire de deux directions.
7) Ecrire une fonction calculant le produit vectoriel de deux directions.
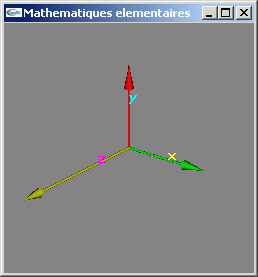


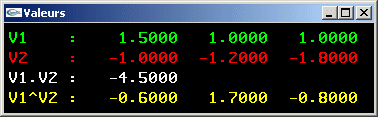
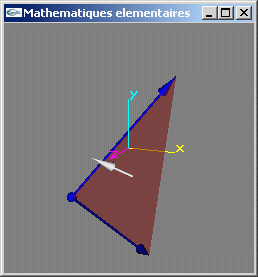
8) Définir une structure de données permettant de stocker une facette triangulaire d'un espace à 3 dimensions.
9) Ecrire une fonction calculant l'une des deux normales à une facette triangulaire.
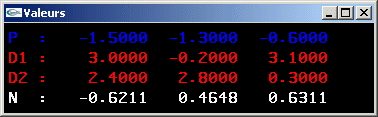
10) Ecrire une fonction testant le parallélisme entre deux facettes triangulaires.
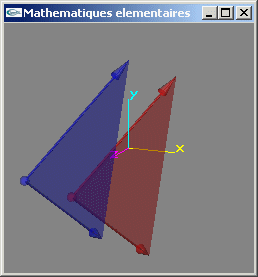
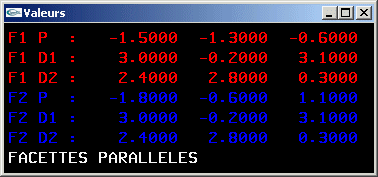
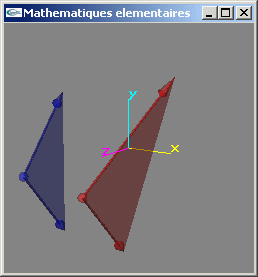
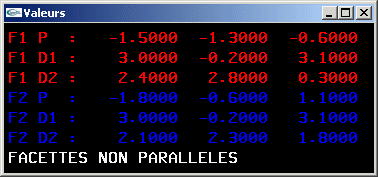
11) Définir une structure de données permettant de stocker une facette d'arité quelconque d'un espace à 3 dimensions.
12) Ecrire une fonction testant la planarité d'une facette d'arité quelconque.
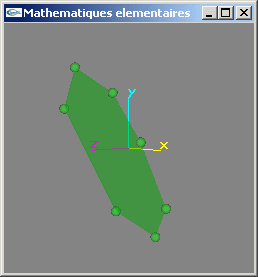



13) Ecrire une fonction testant la convexité d'une facette plane d'arité quelconque.

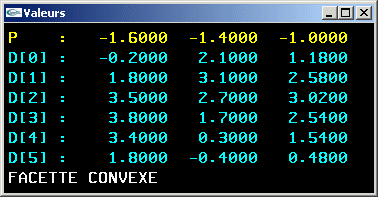
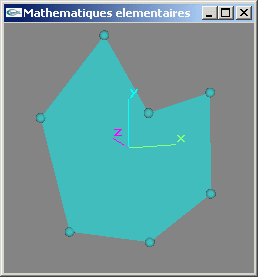
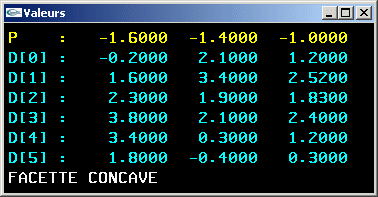
Solution
TD n°7: Le placage de texture en VRML et en OpenGL
Le placage de texture
Application en VRML
Application en OpenGL
Exercice 1 : VRML
Définir le champ image d'un noeud Texture2 permettant la création d'une texture de 2x2 pixels rouge, vert pour la ligne du haut et bleu et jaune pour la ligne du bas.

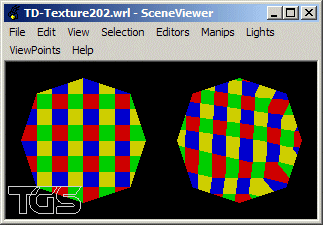
Exercice 2 : OpenGL
a) Définir une fonction créant un tableau à même d'être utilisé dans un appel à glTexImage2D pour spécifier une texture identique à celle de l'exercice 1.

b) Reprendre la question précédente pour créer une bitmap en damier de 8 sur 8 pixels alternativement blanc et noir.
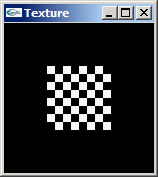
Solution
TD n°8: Le remplissage de cercles et de triangles 2D
Exercice 1
a) Implanter l'algorithme du midpoint (Bresenham) pour le dessin de cercles sur écran raster. On implantera une version simplifiée dessinant des cercles centrés sur l'origine.
b) Ecrire une fonction permettant de tracer le segment horizontal de pixels allant du pixel (-x,y) au pixel (x,y).
c) A partir des fonctions des questions a et b, implanter un algorithme de remplissage de cercles.

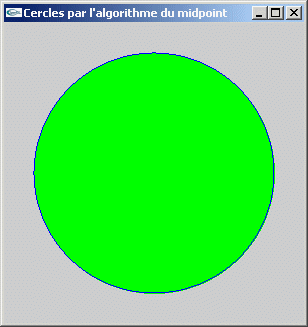
Exercice 2
a) On cherche à déterminer les pixels des bords d'une facette triangulaire définie
dans un espace 2D. Ecrire une fonction permettant de remplir un tableau indicé sur y,
pour tous les y où un segment 2D rectiligne est présent, avec l'abscice d'un des pixels
présent en cet y.
Le prototype de cette fonction pourra être:
int *extractionCote(int xi, int yi, int xf, int yf);
b) Ecrire une fonction permettant de tracer le segment horizontal de pixels allant du pixel (xi,y) au pixel (xf,y).
c) En utilisant les fonctions des questions a et b, écrire une fonction de remplissage
d'une facette triangulaire définie dans un espace 2D.
Le prototype de cette fonction pourra être:
void remplissageFacette(int x1, int y1, int x2, int y2, int x3, int y3);
On pourra supposer les sommets (x1,y1), (x2,y2) et (x3,y3) triés par ordre croissant
d'ordonnée.
Solution
TD n°9: Programmation de classes de gestion des coordonnées homogènes
Le TD est réalisé en java ou en C++.
a) Programmer une classe coordonnées homogènes d'un espace 3D.
b) Programmer une classe position dans un espace 3D.
c) Programmer une classe direction dans un espace 3D.
d) Programmer une classe transformation géométrique en coordonnées homogènes d'un espace 3D.
e) Programmer une classe translation dans un espace 3D.
f) Programmer une classe rotation autour d'un axe arbitraire passant par l'origine.
g) Intégrer à la hiérarchie de classe définie aux questions précédentes une méthode permettant d'appliquer une transformation géométrique à une position ou une direction.
h) Intégrer à la hiérarchie de classe une méthode permettant de composer des transformations géométriques.
Solution
![]()
TP n°1: Prise en mains d'un environnement de programmation VRML
Les viewers disponibles sont:
- Un plugin Internet Explorer/Netscape Navigator (soit Cortona Player, soit Cosmo Player suivant les machines)
- Une application de visualisation (Scene Viewer)
Travail demandé:
- Implantation des fichiers VRML du TD n°1.
- Implantation d'une scène avec un cube, une sphère, un cylindre et un cone pour vérifier le centrage et l'axe de dessin de ces objets.
- Modification du bras robot pour que l'avant bras et le bras soient transformés en cylindres et que l'articulation soit modélisée par un objet supplémentaire de type sphère.

TP n°2: Prise en mains d'un environnement de programmation OpenGL
Création d'un projet Visual C++ permettant la compilation OpenGL (bien spécifier les librairies OpenGL: OpenGL32.lib, glu32.lib et glut32.lib).
Téléchargement du programme source exemple minimum destiné à être testé: BeaucoupTropSimple.cpp.
Téléchargement du programme source exemple fonctionnel (caméra, gestion du clavier, dessin d'une scène) destiné à être testé: OpenGL.cpp.
Téléchargement du programme source exemple (animation) destiné à être testé: Roll.cpp.
Téléchargement du programme source exemple (animation) destiné à être testé: StarWarsIntro.cpp.
Dessin des objets de base GLUt pour repérer leurs caractéristiques de taille, d'orientation et de facettisation.
Implantation des exercices du TD n°2 (en repartant des exemples précédents).
Fichiers sources pour dessiner des cylindres
ModuleCylindres.cpp
ModuleCylindres.h
TP n°3: GLUT
Exercice 1
Programmez une application OpenGL affichant une petite sphère dans une fenêtre et permettant à l'utilisateur de cliquer au moyen de la souris pour déplacer cette sphère à l'endroit où le clic a eu lieu.
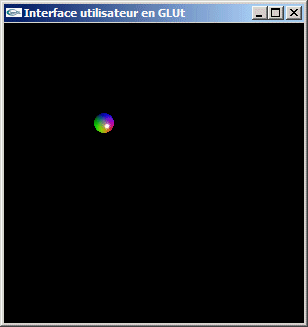
Exercice 2
Programmez une application OpenGL affichant une petite sphère dans une fenêtre et permettant à l'utilisateur de glisser déplacer (drag and drop) cette sphère au moyen de la souris.
Exercice 3
Programmez une application OpenGL affichant une petite sphère dans une fenêtre et permettant à l'utilisateur de cliquer au moyen de la souris pour déclencher une animation amenant la sphère de sa position originelle à la position cliquée. Le déplacement est rectiligne à raison de deux pixels entre images successives. Quand la position destination est atteinte, l'animation s'arrête.
GLUt |
||
| Gestion de la souris, exercice 1 | ||
| Gestion de la souris, exercice 2 | ||
| Gestion de la souris, exercice 3 | ||
Exercice 4
Programmez une animation où une sphère de rayon 1 et un cube de coté 2
sont séparés d'une distance égale à 3 tournent l'un autour de l'autre (autour du point
médian entre eux).
Programmez un contrôle clavier permettant d'activer/désactiver cette animation.

TP n°4: Gestion des caméras en OpenGL
Programmez une animation où deux objets (une sphère de rayon 1 et un
cube de coté 2) sont séparés d'une distance égale à 3 et tournent l'un autour de
l'autre à raison de 1° de rotation entre chaque image. L'animation est réalisée dans
le plan xOy. Elle s'effectue autour du point médian entre les deux objets lui-même
placé à l'origine.
Programmez un contrôle clavier sur la touche espace permettant d'activer/désactiver
cette animation.
Programmez un contrôle clavier sur la touche F2 permettant de visualiser les objets en
fil de fer ou en solide.
a) Progammez cette scène pour qu'elle soit visualisée en projection paralléle orthographique avec une ouvertue verticale de 6 et que le ratio de la fenêtre soit identique au ratio de la caméra de visualisation.

b) Progammez cette scène pour qu'elle soit visualisée en gros plan en projection en perspective depuis le point de coordonnées (0.0, 0.0, 100.0) et que le ratio de la fenêtre soit identique au ratio de la caméra de visualisation.

c) Progammez cette scène pour qu'elle soit visualisée en gros plan en projection en perspective depuis le point de coordonnées (0.0, 0.0, 5.0) et que le ratio de la fenêtre soit identique au ratio de la caméra de visualisation.
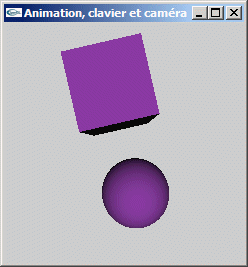
d) Progammez cette scène pour qu'elle soit visualisée en gros plan en projection en perspective depuis le point de coordonnées (5.0, 5.0, 5.0) et que le ratio de la fenêtre soit identique au ratio de la caméra de visualisation.

e) Modifiez la programmation réalisée pour pouvoir utiliser la touche return pour switcher entre les modes de visualisation des questions a, b, c et d.
TP n°5: Les matériaux et lumières en OpenGL
Gestion en OpenGL des matériaux et des lumières
Implanter en OpenGL les exercices du TD n°5.


TP n°6: Mathématiques pour les calculs d'éclairage
Le but du TP est l'implantation des calculs mathématiques nécessaires à la réalisation d'un calcul d'ombrage sur une facette diffusante éclairée par une source lumineuse ponctuelle.
a) Définir les structures C (ou les classes C++) permettant de représenter les
données suivantes:
- une position dans un espace à trois dimensions,
- une direction dans un espace à trois dimensions,
- une facette triangulaire dans un espace à trois dimensions,
- une couleur rvb,
- une source lumineuse ponctuelle colorée,
- un matériel permettant le paramétrage d'une réflexion diffuse.
b) Ecrire et tester les fonctions réalisant les opérations suivantes:
- calcul de la direction définie entre deux positions,
- calcul de la norme d'une direction,
- calcul de la distance entre deux positions,
- normalisation d'une direction,
- calcul du produit scalaire de deux directions,
- calcul du produit vectoriel de deux directions,
- calcul d'une des deux normales à une facette triangulaire.
c) Ecrire et tester une fonction calculant l'énergie lumineuse colorée Ip reçue en
une position depuis une source lumineuse (énergie proportionnelle à la quantité
d'énergie émise et inversement proportionnelle au carré de la distance entre la source
lumineuse et le point considéré).
Les informations connues en entête de fonction sont:
- la position du point où l'énergie reçue est évaluée,
- la source lumineuse ponctuelle colorée émettant de l'énergie.
d) Ecrire et tester une fonction de calcul de l'énergie lumineuse colorée diffusée (formule de Lambert, L = Ip Kd (![]() .
.![]() )) en un point d'une surface.
)) en un point d'une surface.
Les informations connues en entête de fonction sont:
- la position du point où la diffusion est évaluée,
- le matériel dont la surface est munie,
- la source lumineuse ponctuelle éclairant la surface,
- la normale à la surface au point de diffusion.
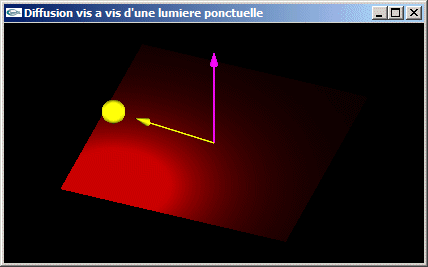
e) Utiliser la fonction de la question (d) pour réaliser le calcul d'éclairage par
diffusion des trois sommets d'une facette triangulaire munie d'un matériel sous une
source lumineuse ponctuelle colorée.
Utiliser le lissage des couleurs
qu'OpenGL peut générer sur une facette pour illustrer l'ombrage complet de la facette.
Solutions
TP n°7: Le clipping par l'algorithme de Cohen-Sutherland
On souhaite implanter l'algorithme de Cohen-Sutherland pour le clipping (découpage) de segments de droite à l'intérieur de rectangles.
a) Définir une structure (ou classe) position d'un espace à deux dimensions.
b) Définir une structure (ou classe) segment de droite d'un espace à deux dimensions.
c) Définir une structure (ou classe) rectangle d'un espace à deux dimensions.
d) Définir une structure (ou classe) code utilisable pour le codage d'une position vis à vis d'un rectangle dans le cadre de l'implantation de l'algorithme de Cohen-Sutherland.
e) Implanter les fonctions (ou méthodes) de gestion de code utilisées pour l'implantation de l'algorithme de Cohen-Sutherland:
- calcul du code d'une position vis à vis d'un rectangle,
- test de l'"égalité à zéro" intégrale d'un code,
- calcul du "et binaire" entre deux codes,
- test du nième booléen d'un code.
f) Implanter une fonction (ou méthode) permettant de calculer la position de l'intersection entre la droite soutendue par un segment et une droite horizontale d'ordonnée y.
g) Implanter une fonction (ou méthode) permettant de calculer la position de l'intersection entre la droite soutendue par un segment et une droite verticale d'abscisse x.
h) Implanter et tester l'algorithme de Cohen-Sutherland.