Sujets et Corrections
de TD et TP
![]()
TD n°1
Création de scènes
en VRML 1.0
TD n°2
Premières scènes
OpenGL
TP n°1
Prise en mains
d'un environnement
de programmation
VRML
TD n°3
Modélisation
géométrique
en OpenGL
au moyen
d'objets canoniques
ou de facettes
TP n°2
Prise en mains
d'un environnement
de programmation
VRML
TD n°4
Gestion des caméras
en VRML
TP n°3
Programmation
événementielle
en OpenGL
avec GLUt
TD n°5
Gestion des caméras
en OpenGL
TP n°4
Gestion des caméras
en OpenGL
TD n°6
Matériaux
et lumières
en VRML
TP n°5
Matériaux
et lumières
en OpenGL
TP n°6
Mathématiques
de l'Infographie :
Mathématiques
matricielles
TP n°7
Mathématiques
de l'Infographie :
Implantation de
transformations
géométriques
de visualisation
TD n°7
Algorithmique
de l'Infographie :
Dessin d'un segment
de droite
TP n°8
Algorithmique
de l'Infographie :
Remplissage d'une
facette triangulaire
TD n°8
Calculs
mathématiques
pour le lancer
de rayons
TP n°10
Calculs
mathématiques
pour le lancer
de rayons
Dernière modification
19/11/09 08:27:13
Quatre sphères de rayon 1.0 aux positions (2.0,0.0,2.0), (2.0,0.0,-2.0), (-2.0,0.0,2.0) et (-2.0,0.0,-2.0).e suivante sans utiliser le nœud Separator ailleurs que pour le Separator d'encadrement global du fichier:
Quatre sphères de rayon 1.0 aux positions (2.0,0.0,2.0), (2.0,0.0,-2.0), (-2.0,0.0,2.0) et (-2.0,0.0,-2.0).
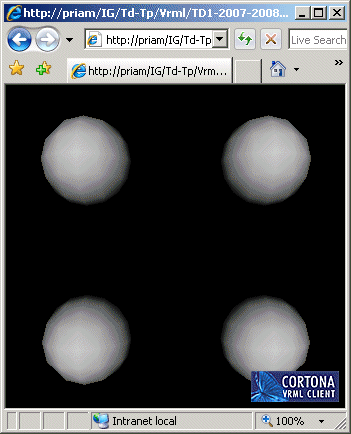
(2) Reprogrammer en VRML la scène de la question (1) en utilisant le nœud Separator pour rendre les objets indépendants les uns des autres.
(3) Reprogrammer en VRML la scène en apportant les modifications suivantes:
- La sphère en position (2.0,0.0,-2.0) subit une rotation de -45° autour de l'axe y passant par son centre.
- La sphère en position (2.0,0.0,2.0) subit un zoom de rapport (0.5,1.0,2.0) par rapport à son centre.
- La sphère en position (-2.0,0.0,2.0) n'est plus centrée en ce point. Elle est placée de telle manière qu'elle présente une rotation de 30° autour de l'axe y passant par le sommet (-2.0,0.0,2.0) et que ce sommet soit sur sa surface. En outre, elle subit un zoom de rapport (0.5,1.0,1.0) par rapport à son centre.

Solutions
![]()
TD n°2: Premières scènes OpenGL
Exercice 1
Implanter en OpenGL la question n°3 du TD n°1.
Exercice 2
Programmer la scène modélisant un bras robot composé d'un avant-bras et
d'un bras.
L'avant-bras est articulé pour tourner autour de l'axe y d'un angle r1. Il s'agit d'un
parallélépipède rectangle de dimension (3.0,1.0,1.0) (en rouge sur le shéma du TP n°1
ci-dessous).
Le bras est articulé autour de l'axe y au bout de l'avant bras pour un angle r2. Il
s'agit d'un parallélépipède rectangle de dimension (3.0,0.8,0.8) (en vert sur le shéma
du TP n°1).
![]()
TP n°1: Prise en mains d'un environnement de programmation VRML
Les viewers disponibles sont:
- Un plugin Internet Explorer/Netscape Navigator (Cortona Player)
- Une application de visualisation (Scene Viewer)
Travail demandé:
- Implantation des fichiers VRML du TD n°1.
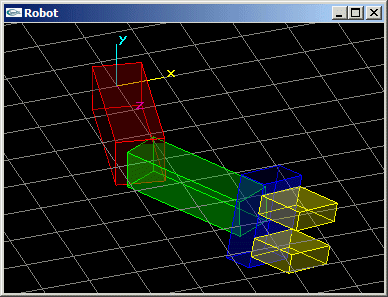
- Programmer la scène modélisant un bras robot composé d'un avant-bras, d'un bras, et
d'une paire de pinces.
L'avant-bras est articulé pour tourner autour de l'axe y d'un angle r1. Il s'agit d'un parallélépipède rectangle de dimension (3.0,1.0,1.0) (en rouge sur le shéma ci-dessous).
Le bras est articulé autour de l'axe y au bout de l'avant bras pour un angle r2. Il s'agit d'un parallélépipède rectangle de dimension (3.0,0.8,0.8) (en vert sur le shéma).
La pince est située au bout du bras. Elle peut tourner autour de l'axe du bras pour un angle r3. L'embase de la pince est un parallélépipède rectangle de dimension (0.6,1.2,1.8) (en bleu sur le shéma).
Chacune des mâchoires est un parallélépipède rectangle de dimension (1.0,1.2,0.4) (en jaune sur le shéma) à même de se déplacer longitudinalement d'une valeur d pour réaliser une ouverture totale de 2xd.
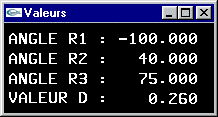
- Modification du bras robot pour que l'avant bras et le bras soient transformés en cylindres de diamètre 1.0 et 0.8 et de hauteur 3.0 et que l'articulation soit modélisée par un objet supplémentaire de type sphère de diamètre 1.4.
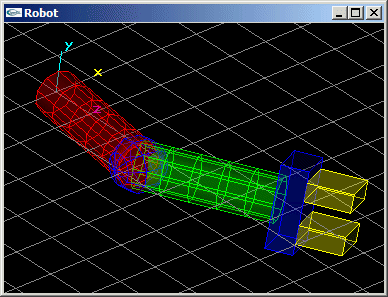
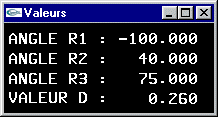
- Nouvelle modification du bras robot pour que les mandibules soient transformées en des cônes de rayon 0.2 et de hauteur 2.0 pointant vers l'intérieur de la pince avec un angle de r4 radians par rotation autour du centre de leurs bases.


Solutions
| Scène (2) |
| Scène (3) |
| Le bras robot |
| Le bras robot avec cylindres |
| Le bras robot avec cylindres et cones |
![]()
Exercice 1: Modélisation à base d'objets canoniques
Dans le cadre d'un programme informatique de simulation d'un accélérateur de particules développé pour le CERN (Centre Européen pour la Recherche Nucléaire), on souhaite concevoir une fonction permettant de dessiner un assemblage de parallélipipèdes rectangles selon les caractéristiques suivantes:
n cubes de coté 1 sont placés centrés aux sommets d'un polygone virtuel régulier de rayon 10.0, centré sur l'origine, placé dans le plan xOy. Chacun de ces cubes présente une face orientée vers l'origine du repère.
n parallélipidèdes rectangle de section (0.5, 0.5) sont placés pour relier chaque paire de cubes consécutifs.
Dans la figure ci-dessous, n est égal à 10 (l'affichage est réalisé en projection en perspective).
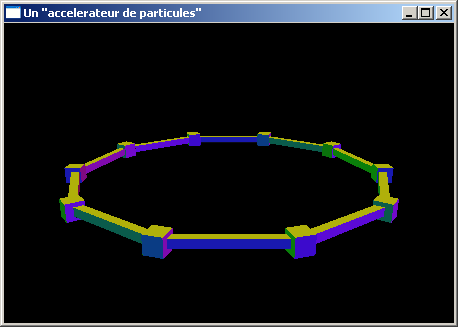
Développer une fonction void scene(int n) réalisant la modélisation géométrique de ces 2*n "cubes".
Exercice 2: Modélisation par facettes
La fonction void glutSolidCube(double c) de la librairie glut modélise un
cube de largeur, hauteur et profondeur identiques égales à la valeur c.
Développer une fonction void myBox(float tx,float ty,float tz) modélisant par facettes
un parallélipipède rectangle de largeur tx, de hauteur ty et de profondeur tz.
![]()
TP n°2: Prise en mains d'un environnement de programmation OpenGL
Création d'un projet Visual C++ permettant la compilation OpenGL
- Les fichiers d'inclusion (nécessaires à la compilation) spécifiques à OpenGL sont GL/gl.h et GL/glu.h ainsi que GL/glut.h si GLUT est utilisé.
- Les librairies d'édition de liens (nécessaires à la création de l'exécutable) spécifiques à OpenGL sont OpenGL32.lib et glu32.lib ainsi que glut32.lib si GLUT est utilisé.
- Les dll (nécessaires à l'exécution) spécifiques à OpenGL sont OpenGL32.dll et glu32.dll ainsi que glut32.dll si GLUT est utilisé.
Seul GLUT n'est pas installé lors de l'installation de Visual C++. Il est nécessaire de se procurer les fichiers .h, .lib et .dll lui correspondant puis de les installer.
Les librairies OpenGL32.lib et glu32.lib spécifient des fonctions situées dans OpenGL32.dll et glu32.dll spécifiques à la carte graphique installée.Suivant la manière avec laquelle Visual C++ à été installé, il pourra être nécessaire (ou non) de spécifier les fichiers .lib d'OpenGL dans les options de linkage.
Si gcc sous Linux est utilisé, Mesa3D devrait avoir été installé au cours de l'installation des outils de développement (gcc). S'il ne l'est pas, ou si l'on constate l'absence de GLUT, ou si l'on souhaite utiliser une version plus récente que celle disponible (en septembre 2007, la version la plus récente disponible de Mesa3D est la version 7.0.1 qui est compatible OpenGL 2.1), il sera nécessaire de télécharger et d'installer (compilation puis installation, une archive pour OpenGL, une archive pour GLUT et une archive pour des exemples) la version souhaitée.
Pour l'édition de lien d'un exécutable OpenGL & GLUT, il est nécessaire de spécifier les librairies GL, GLU et glut dans la ligne de commande de compilation.
Téléchargement du programme source exemple, compilation et exécution: Affichage-Informations-Release.cpp.
Exécutable compilé avec Visual C++ et l'OpenGL de Visual C++

Exécutable compilé avec Visual C++ et l'OpenGL Mesa3D
Téléchargement du programme source exemple (animation) destiné à être testé: Animation2008-2009.cpp.

- Implantation des exercices du TD n°3
![]()
TD n°4: Gestion des caméras en VRML
Exercice n°1
On considère une scène quelconque centrée sur l'origine du repère.
On souhaite visualiser cette scène de telle manière que son centre soit affiché au
centre de la fenêtre d'affichage.
Notre caméra de visualisation "regarde" par défaut selon l'axe -z. Une seule
rotation est autorisée pour l'orienter selon la direction souhaitée. Cette rotation peut
être définie selon n'importe quel axe (i.e. pas forcément uniquement (1, 0, 0), (0, 1,
0) ou (0, 0, 1), mais aussi tout axe (dx, dy, dz) tel que dx, dy et dz non nuls
simultanément) et n'importe quel angle
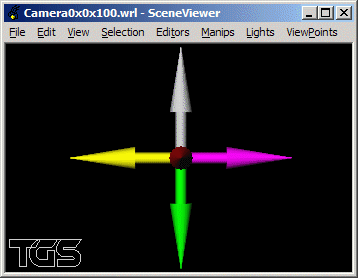
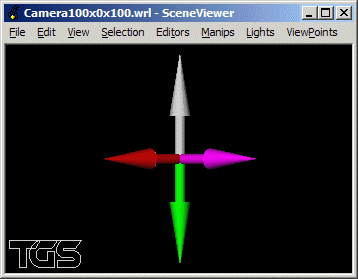
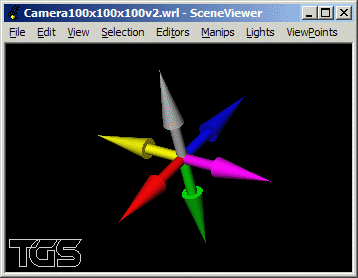
Définir la rotation à réaliser pour chacun des 4 points de vue
(position de la caméra) suivants:
(a) (0.0, 0.0, 100.0),
(b) (0.0, 0.0, -100.0),
(c) (100.0, 0.0, 100.0),
(d) (100.0, 100.0, 100.0).
|
|
|
|
Exercice n°2
On souhaite implanter les 4 points de vue de l'exercice n°1 dans le cadre
de 4 fichiers VRML.
La caméra choisie est la caméra de visualisation en perspective. La scène possède un
rayon voisin de 5. On souhaite la visualiser en "gros plan".
Définir les noeuds caméra que vous utiliseriez.
Solutions
![]()
TP n°3: Programmation événementielle en OpenGL avec GLUT
Fichier pdf des spécifications de GLUt version 3 : GLUt.pdf
Le programme OpenGL-GLUt.cpp intègre la gestion d'une fenêtre d'affichage, d'une animation, du clavier, des touches de curseur du clavier ainsi que de la souris.
GLUT |
||
| Programmation OpenGL + GLUt pour l'animation et la gestion de contrôles clavier et souris |
||
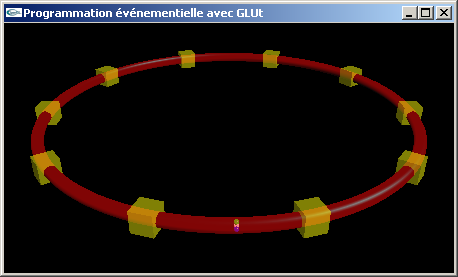
- Télécharger, compiler et exécuter ce programme.
- Déterminer quels sont les contrôles effectivement implantés.
- Déterminer en quoi consiste l'animation réalisée.
- Ajouter un contrôle clavier permettant de faire tourner la scène sur elle-même autour de l'axe Ox.
- Ajouter un contrôle souris permettant de déplacer et de zoomer la scène.
Solutions
GLUT |
||
| Ajout à OpenGL-GLUt.cpp du contrôle clavier permettant la rotation de la scène autour de l'axe Ox | ||
| Ajout à la solution précédente du contrôle
souris permettant le zoom et la translation de la scène Zoom par un scale de la scène |
||
| Ajout à la solution précédente du contrôle
souris permettant le zoom et la translation de la scène Zoom par paramétrage de la "position" de la caméra (gluLookAt) |
||
| Ajout à la solution précédente du contrôle
souris permettant le zoom et la translation de la scène Zoom par paramètrage de l'angle d'ouverture de la caméra (gluPerspective) |
||
![]()
TD n°5: Gestion des caméras en OpenGL
On dispose d'une scène modélisée au sein d'une fonction void scene(void). Cette scène est modélisée centrée sur le repère courant et occupe un "volume sphérique" de rayon 12.0.

Exercice n°1
Implanter la fonction reshape d'un programme OpenGL + GLUt permettant de visualiser cette scène au moyen d'une caméra de visualisation en perspective placée à l'origine, orientée selon la direction -z en respectant une distance de 100.0 entre la caméra et la scène.

Exercice n°2
Modifier la fonction reshape précédente pour que la caméra reste placée à l'origine, mais regarde la scène déplacée en position (-100.0,-100.0,-100.0).
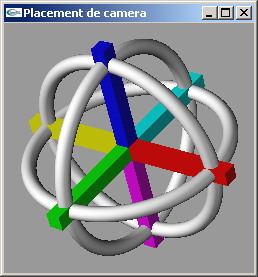

Deux solutions admissibles parmi toutes celles possibles
Exrecice n°3
Modifier la fonction reshape précédente pour transformer la caméra en une caméra de
visualisation en projection parallèle orthographique définie selon les mêmes
caractéristiques de placement et d'orientation.
Rapprocher la caméra d'un facteur 5 pour constater l'absence de grossissement et de
déformation.

Solutions
GLUT |
||
| Exercice n°1 Scène placée en (0.0, 0.0, -100.0) avec caméra en position (0.0, 0.0, 0.0) |
||
| Exercice n°2 Scène placée en (-100.0, -100.0, -100.0) avec caméra en position (0.0, 0.0, 0.0) |
||
| Exercice n°2 : Solution alternative | ||
| Exercice n°2 : Solution avec gluLookAt | ||
| Exercice n°3 : Projection parallèle orthographique | ||
| Exercice n°3 : Rapprochement d'un facteur 5 | ||
| Exercice n°3 : Projection en perspective rapprochée | ||
![]()
TP n°4: Gestion des caméras en OpenGL
Exercice n°1
Le fichier Scene.cpp (décrit par le fichier d'entête Scene.h) contient une fonction void scene(int l) de modélisation d'une scène composée d'une surface plane carrée de diagonale (-10.0, 0.0, -10.0) - (10.0, 0.0, 10.0) sur laquelle sont posés aléatoirement 100 "poteaux" parallélipipédiques. L'éclairage de cette scène est activé/désactivé par le paramètre "booléen" l.

Implanter le dessin de cette scène par une caméra de visualisation en perspective placée en position (0.0, 0.5, 0.0) orientée selon la direction de visualisation (0.0, 0.0, 1.0). L'ouverture verticale de la caméra est de 60°. Les plans cmin est cmax sont aux distances 0.1 et 100.0. La taille de la fenêtre d'affichage est 450 sur 200 pixels.
Exercice n°2
Modifier le programme précédent pour autoriser le déplacement de la caméra au moyen des touches up et down de manière à avancer et reculer dans la scène dans l'axe de la caméra.
Exercice n°3
Modifier le programme précédent pour autoriser l'utilisation des touches right et left de manière à faire tourner la caméra vers la droite et vers la gauche tout en continuant à pourvoir utiliser les touches up et down pour avancer et reculer.
Exercice n°4
Modifier le programme précédent pour autoriser l'utilisation de la souris de manière à tourner la caméra vers la droite et vers la gauche et à la faire avancer vers l'avant et vers l'arrière.
Solution
GLUt |
||
| Placement d'une caméra | ||
| Déplacement d'une caméra d'avant en arrière au moyen du clavier | ||
| Déplacement d'une caméra d'avant en arrière et rotation à droite et à gauche au moyen du clavier | ||
| Déplacement d'une caméra d'avant en arrière et rotation à droite et à gauche au moyen du clavier ou de la souris | ||
![]()
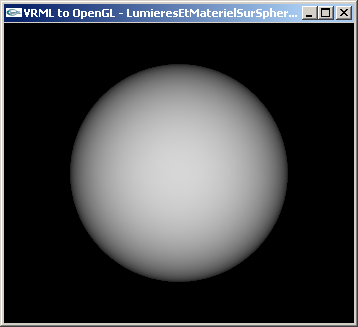
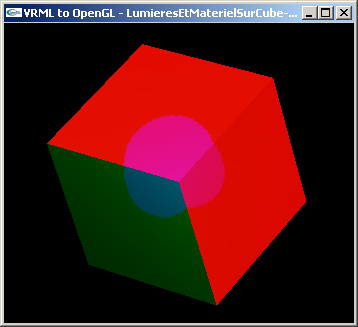
TD n°6: Matériaux et lumières en VRML
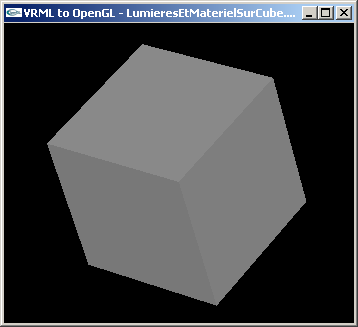
Si le viewer VRML utilisé ne fournit pas des résultats jugés comme étant de qualité suffisante, WRL2OGL peut être utilisé à la place.
Les deux fichiers suivants contiennent des scènes minimum constituées pour la premiére d'une caméra et d'un cube après une rotation, et pour la seconde, d'une caméra et d'une sphère.
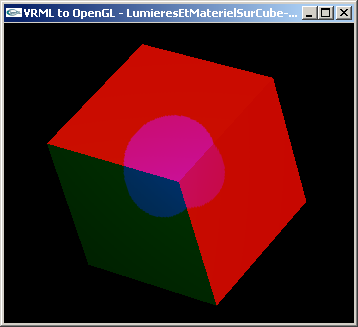
Exercice n°1 : Diffusion
Modifier chacun des deux fichiers pour y ajouter 3 lumières et un matériel selon les caractéristiques suivantes:
- 1ère lumière : Type directionnel, intensité 2, couleur rouge, direction (-1.0, -1.0, -1.0)
- 2ème lumière : Type ponctuel, intensité 1, couleur vert, position (-5.0, -5.0, 15.0)
- 3ème lumière : Type spot, intensité 1, couleur bleu, position (-1.0, 1.0, 15.0), orienté vers l'origine, ouverture 0.15 radian
- Matériel : rien en ambiant, rien en spéculaire, rien en émission, (0.6, 0.2, 0.8) en diffusion
|
|
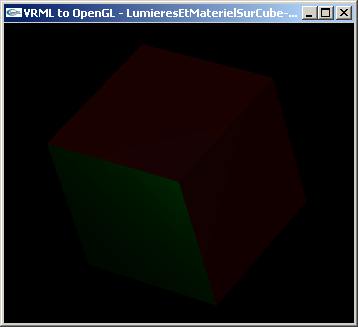
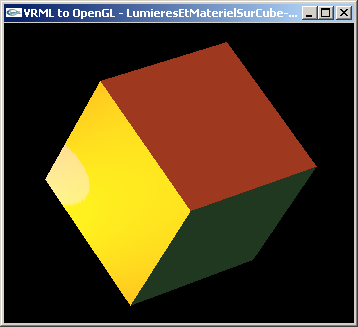
Exercice n°2 : Réflexion spéculaire
Modifier le matériel de chacun des deux fichiers selon les caractéristiques suivantes:
- cube : rien en ambiant, rien en émission, rien en diffusion, (0.4, 0.8, 0.2) en spéculaire, 0.05 en réflectivité
- sphère : rien en ambiant, rien en émission, rien en diffusion, (0.4, 0.8, 0.2) en spéculaire, 0.25 en réflectivité
|
|
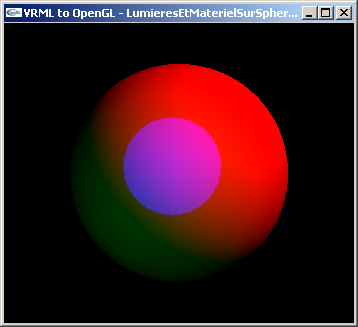
Exercice n°3 : Fusion des deux composantes "diffusion" et "réflexion spéculaire"
Modifier le matériel de chacun des deux fichiers précédents pour reprendre coefficients de diffusion et de réflexion spéculaire et laisser l'ambient et l'émission à zéro.
|
|
Exercice n°4 : Ajout de composantes ambiente et en émission
Modifier une dernière fois les fichiers précédents pour définir la composante ambiente du matériel avec la valeur (0.1, 0.1, 0.1) et la composante émissive avec la valeur (0.1, 0.2, 0.1). Tourner la scène pour visualiser l'influence de ces composantes sur les zones non éclairées par les trois lumières.
|
|
Solutions
![]()
TP n°5: Matériaux et lumières en OpenGL
Matériaux et lumières en OpenGL
Implanter en OpenGL les exercices du TD n°5.
Solution
GLUt |
||
| Trois lumières et un matériel diffusant sur une sphère ou un cube | ||
| Trois lumières et un matériel réfléchissant spéculairement sur une sphère ou un cube | ||
| Trois lumières et un matériel diffusant et réfléchissant spéculairement sur une sphère ou un cube | ||
| Trois lumières et un matériel diffusant et réfléchissant spéculairement + réponse aux éclairages ambiant + émission sur une sphère ou un cube | ||
![]()
TP n°6: Mathématiques de l'Infographie : Mathématiques matricielles
Ce TP est à réaliser en C++ ou en Java.
Exercice n°1
- Implanter une classe "minimum" CoordonneesHomogenes3D.
- Dériver la classe CoordonneesHomogenes3D en une classe Position3D.
- Dériver la classe CoordonneesHomogenes3D en une classe Direction3D.
Exercice n°2
- Implanter une classe "minimum" TransformationGeometrique3D.
- Dériver la classe TransformationGeometrique3D en une classe Translation3D.
- Dériver la classe TransformationGeometrique3D en une classe Rotation3D.
- Dériver la classe TransformationGeometrique3D en une classe Scale3D.
Exercice n°3
- Implanter la transformation d'une position par une transformation géométrique.
- Implanter la transformation d'une direction par une transformation géométrique.
- Implanter la composition de 2 transformations géométriques en une transformation géométrique.
Programme de test |
![]()
TP n°7: Mathématiques de l'Infographie : Implantation de transformations géométriques de visualisation
Exercice n°1
Les classes Java suivantes vous sont fournies:
Pages WEB de référence au format Javadoc pour ces classes
- Afficheur (interface)
- AfficheurProjectionOrthographique (classe implantant l'interface précédente)
- ApplicationFrame (classe dérivant de Frame pour créer et gérer une fenêtre)
- ApplicationCanvas (classe dérivant de Canvas pour créer et gérer un canvas d'affichage)
- ThreadTacheDeFond (classe dérivant de Thread pour implanter une tâche de fond)
- ProjectionOrthographique (classe principale contenant la fonction principale static main)
Pages WEB de référence au format Javadoc pour ces classes
Les 4 premières implante la gestion des coordonnées homogènes 3D et les
transformations géométriques sur ces coordonnées homogènes.
Les 5 suivantes implante une application Java (ProjectionOrthographique) affichant une
animation où un objet est affiché en fil de fer visualisé par une caméra virtuelle
tournant autour. La caméra réalise une projection parallèle orthographique. l'AWT
(Abstract Window Toolkit) java est utilisé pour construire l'interface utilisateur
(fenêtre et canvas d'affichage, menus, gestion événementielle, ...).

La classe AfficheurProjectionOrthographique fait appel à une classe appelée Ortho non fournie. Le but de l'exercice consiste à développer cette classe par dérivation de la classe TransformationGeometrique3D de manière qu'elle assure le calcul de la matrice de transformation de mise en projection orthographique définie par les conditions initiales suivantes:
- position de l'observateur,
- position d'un point visé,
- verticales (axe y) "conservées" dans le repère écran.
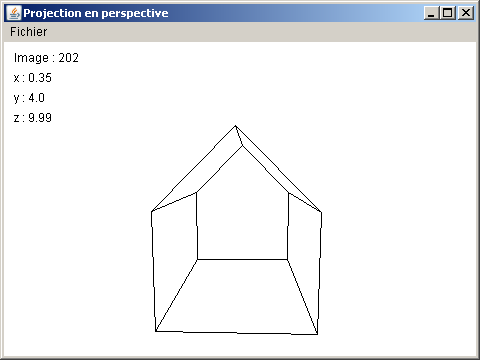
Exercice n°2
Dans l'exercice précédent, la méthode public void paint(Graphics g,int numeroImage,int tx,int ty) de la classe AfficheurProjectionOrthographique réalise les opérations nécessaires au dessin d'une image de l'animation (hors effacement du canvas réalisé automatiquement par ailleurs). Elle pourrait être vue comme l'équivalent des fonctions reshape et display d'un programme OpenGL+GLUt écrites en une seule fonction.
Vous disposez seulement de la classe principale suivante:
La classe AfficheurProjectionPerspective ne vous est pas fournie. Le but de l'exercice
consiste à développer cette classe (elle doit implanter l'interface Afficheur) dans le
but de dessiner la même scène que celle de l'exercice n°1 animée selon le même
déplacement de caméra que l'exercice n°1 mais en réalisant un affichage par projection
en perspective.
On pourra s'inspirer de la classe AfficheurProjectionOrthographique et développer une
classe Persp dérivée de TransformationGeometrique3D pour calculer la matrice de
transformation pour mise en perspective.
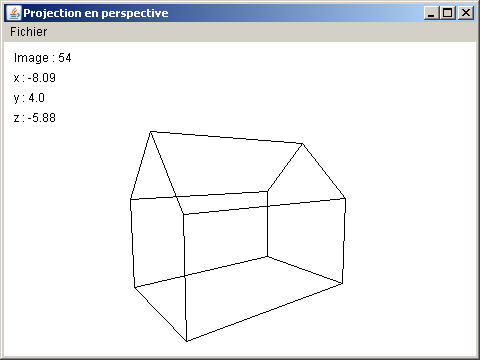
Solutions
![]()
TD n°7: Algorithmique de l'Infographie : Dessin d'un segment de droite
Exercice n°1
L'algorithme suivant rastérise le segment de droite 2D défini par les extrémités (xi,yi) et (xf,yf) sur un écran 2D en 8-connexité.
Hypothèses: xf > xi, yf >= yi, xf - xi > yf - yi
void ligne(int xi,int yi,int xf,int yf) {
int dx,dy,cumul,x,y ;
x = xi ;
y = yi ;
dx = xf - xi ;
dy = yf - yi ;
allume_pixel(x,y) ;
cumul = dx / 2 ;
for ( x = xi+1 ; x <= xf ; x++ ) {
cumul += dy ;
if (cumul >= dx) {
cumul -= dx ;
y += 1 ; }
allume_pixel(x,y) ; }
}
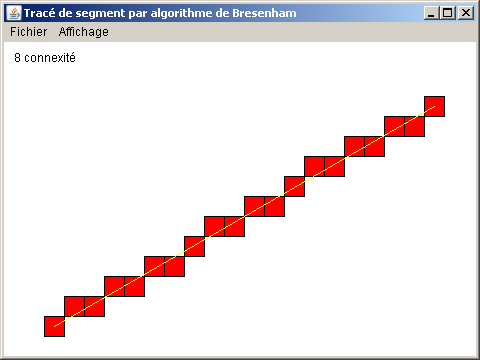
Modifier cet algorithme pour qu'il dessine en 4-connexité.

Solution imparfaite : Les pixels ajoutés le sont
systèmatiquement en position inférieure.

Meilleure solution : Les pixels ajoutés sont placés
pour recouvrir le segment continu.
Exercice n°2
Reprendre l'algorithme initial de l'exercice n°1 pour le généraliser à la rastérisation d'un segment de droite 3D dans un espace voxel 3D en 26-connexité.

Solutions
|
||||||||
|
||||||||
![]()
TP n°8: Algorithmique de l'Infographie : Remplissage d'une facette triangulaire
On souhaite réaliser le remplissage d'une facette triangulaire 2D dont les trois sommets sont situés aux positions (5, 17), (2, 2) et (21, 13).
Sur la base du framework proposé en solution du TP n°7, développer un Afficheur réalisant le dessin de cette facette.
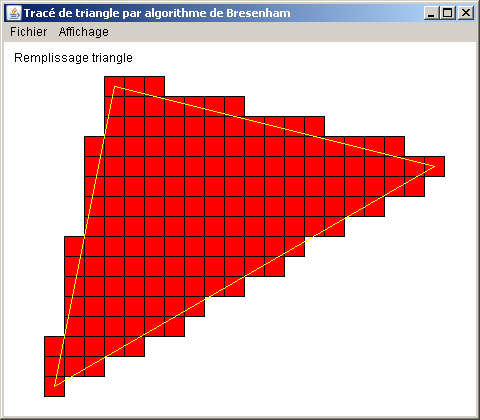
Une première approche de ce problème pourra consister à dessiner la facette en fil de fer, puis à modifier le programme obtenu pour opérer le remplissage.

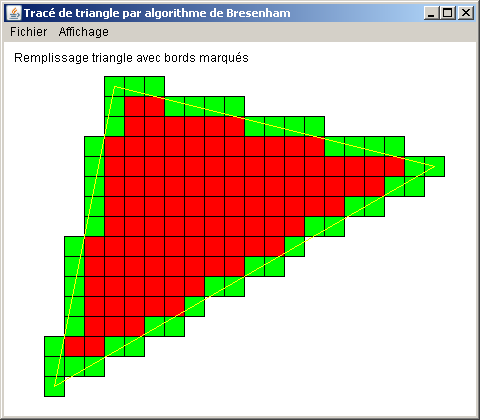
Solutions
|
|||||||
![]()
TD n°8: Calcul de l'intersection entre une sphère et un rayon, des rayons réfléchi et transmis dans le cadre de l'implantation d'un algorithme de lancer de rayons
Le TD est réalisé en langage C. Les structures suivantes devront être utilisées:
- typedef struct position {
double x;
double y;
double z;
double t; } position; - typedef struct direction {
double x;
double y;
double z;
double t; } direction; - typedef struct sphere {
position centre;
double rayon; } sphere; - typedef struct rayonLumineux {
position origine;
direction direction; } rayonLumineux;
a) Implanter une fonction permettant de tester l'existence d'une intersection entre un rayon lumineux et une sphère.
b) Implanter une fonction permettant de déterminer, si elle existe, la distance entre le point d'émission d'un rayon lumineux et l'intersection entre ce rayon et une sphère.
c) Implanter une fonction permettant de calculer la direction du rayon réfléchi créé par un rayon incident à l'interface entre deux milieux.
d) Implanter une fonction permettant de calculer la direction du rayon transmis créé par un rayon incident à l'interface entre deux milieux.
![]()
TP n°9: Le plaçage de texture en OpenGL
Exercice
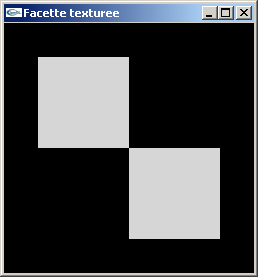
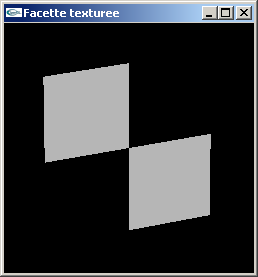
Implanter un programme OpenGL réalisant l'affichage d'une facette carrée de coté de
longueur 8.0 centrée sur l'origine du repère de modélisation.
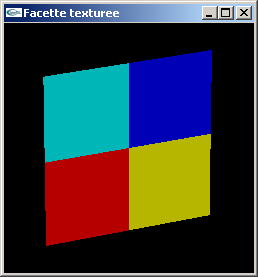
Cette facette sera texturée au moyen d'une texture bitmap 2D de 2x2 pixels blancs et
noirs organisés en damier. Un autre texture de 2x2 pixels rouge, jaune, cyan et bleu
pourra être utilisée.

Solution
GLUt |
||
| Texturage d'une facette carrée | ||
![]()
TD n°9: Courbes lissées
Les courbes et surfaces lissées
Exercice n°1
On donne les 8 sommets suivants définis en 3D:
- (-3.0, -3.0, -3.0)
- (-2.0, 3.0, 1.0)
- (0.0, 3.0, -2.0)
- (3.0, 0.0, -3.0)
- (-2.0, -1.0, 2.0)
- (3.0,-3.0, -1.0)
- (2.0, 3.0, 3.0)
- (0.0, 0.0, 0.0)
Ecrire un programme calculant et affichant la courbe de Bezier correspondant à cette suite de sommets.
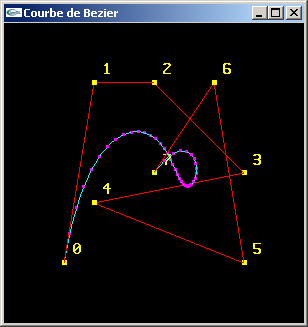
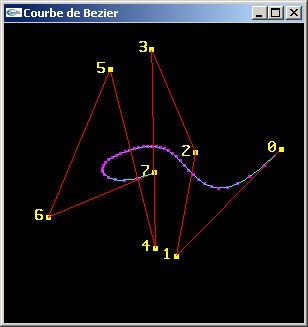
Exercice n°2
On considère les 8 sommets de l'exercice n°1. Ecrire un programme calculant et affichant les courbes B-Splines NRU et Catmull-Romm correspondant aux 5 quadruplets de sommets consécutifs extraits de cette suite de sommets.

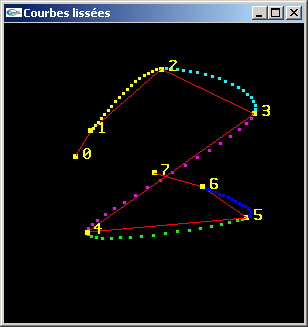
Solution
GLUt |
||
| Des courbes lissées | ||
![]()
TP n°10: Calcul de l'intersection entre une sphère et un rayon, des rayons réfléchi et transmis dans le cadre de l'implantation d'un algorithme de lancer de rayons
Le fichier RayTracing.zip contient un
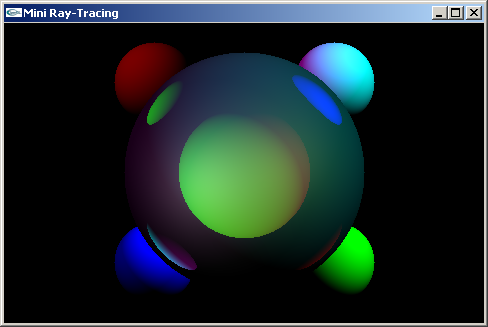
programme de calcul et d'affichage de scènes représentées en lancer de rayons.
Ces scènes sont constituées exclusivement de sphères diffusantes, réfléchissantes et
transparentes. Elles sont éclairées par des lumières ponctuelles ou directionnelles.
Un certain nombre de fonctions ont été vidées de leur contenu.
Le but du TP consiste à développer ces fonctions:
- Fichier RayTracing-Sphere.cpp :
- int intersection(rayonLumineux *rl,sphere *sp,double *d);
- int intersection(rayonLumineux *rl,sphere *sp);
- Fichier RayTracing-Direction.cpp :
- void reflexion(direction *r,direction *i,direction *n);
- int transmission(direction *t,direction *i,direction *n, double niSurnt);
- double produitScalaire(direction *d1,direction *d2);
- void normalise(direction *d);
- void calculDirectionNormalisee(direction *d,position *p1,position *p2);
- Fichier RayTracing-Position.cpp :
- double carreDistance(position *p1,position *p2);
- double distance(position *p1,position *p2);
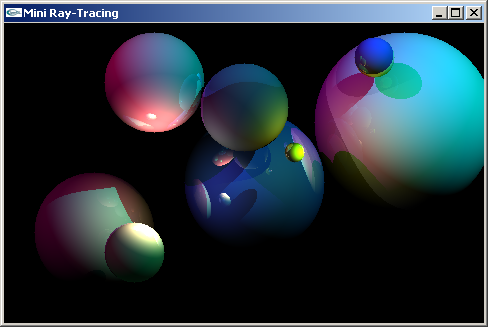
Solution
![]()