Sujets et Corrections
de TD et TP
![]()
|
Fichier zip |
TD n°1 : Premières scènes OpenGL
Exercice n°1
(1) Programmer en OpenGL la scène suivante sous la forme d'une fonction C sans utiliser les fonctions glPushMatrix et glPopMatrix ailleurs
qu'en début et fin de fonction:
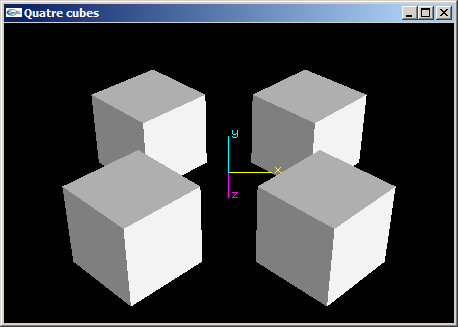
Quatre cubes de coté 2.0 aux positions (2.0,0.0,2.0), (2.0,0.0,-2.0), (-2.0,0.0,2.0) et (-2.0,0.0,-2.0).
(2) Reprogrammer en OpenGL la scène de la question (1) de telle manière que les cubes aient une de leurs faces orientée vers l'origine du repère.
(3) Reprogrammer en OpenGL la scène de la question (2) en utilisant les fonctions glPushMatrix et glPopMatrix pour rendre les objets indépendants les uns des autres et simplifier l'écriture de la fonction scène.
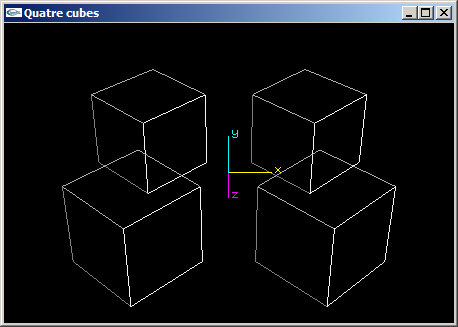
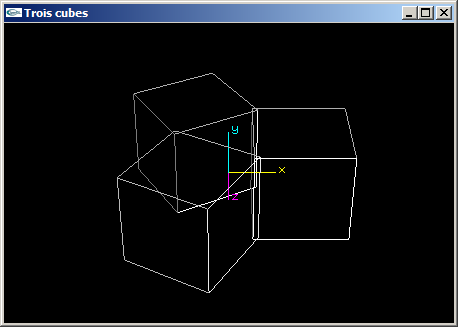
(4) Programmer une scène OpenGL en plaçant 3 cubes de coté 2.0 aux 3 sommets d'un triangle équilatéral défini
avec les caractéristiques suivantes:
- rayon 1.5,
- centré sur l'origine,
- plongé dans le plan xOz.
Les 3 cubes présentent une de leurs faces orientée vers l'origine.

Exercice n°2
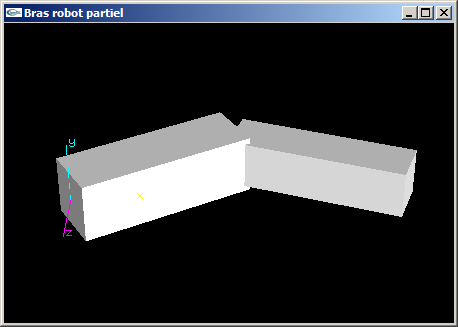
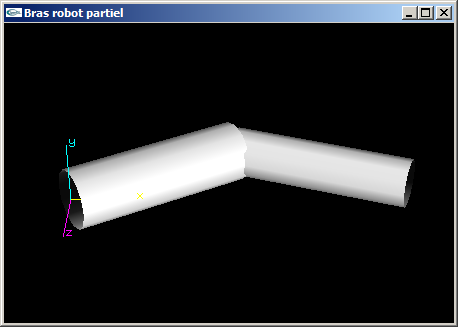
(1) Programmer la scène OpenGL modélisant un bras robot simplifié composé d'un avant-bras et d'un bras.
L'avant-bras est articulé pour que sa base puisse tourner autour de l'axe Oy d'un angle r1. Il s'agit d'un parallélépipède
rectangle de dimension (3.0,1.0,1.0).
Le bras est articulé autour de l'axe y au bout de l'avant bras pour un angle r2. Il s'agit d'un parallélépipède rectangle
de dimension (3.0,0.8,0.8).

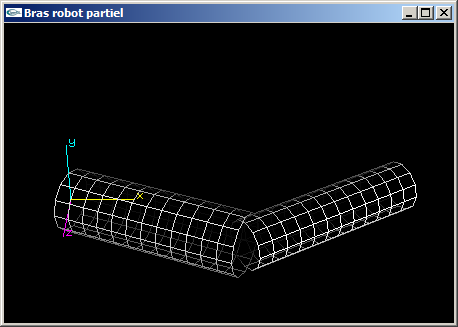
(2) Modifier la fonction OpenGL de l'exercice n°1 en remplaçant les parallélépipèdes par des cylindres de tailles équivalentes.
Exercice 3
a) Implanter en OpenGL une fonction de dessin d'une molécule de Benzène (C6H6).

Les atomes de carbone (atomes centraux) ont un rayon égal à 0.5.
Les liaisons entre 2 atomes de carbone ont pour longueur (centre à centre) 2.0 et pour rayon 0.15.
Les atomes d'hydrogène ont un rayon égal à 0.25.
Les liaisons entre atome de carbone et d'hydrogène ont pour longueur (centre à centre) 1.2 et pour rayon 0.05.
La molécule est centrée sur l'origine et placée dans le plan xOy.
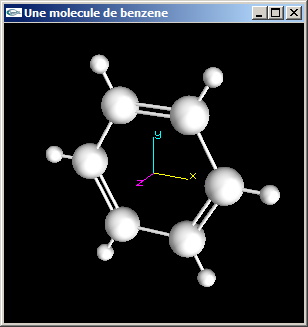
b) Modifier la modélisation de la molécule de benzène de la question précédente pour que les liaisons carbone-carbone
soient alternativement des liaisons simples et des liaisons doubles (voir figure ci-dessous).
Les cylindres modélisant ces liaisons auront pour rayon 0.05 (comme les liaisons carbone-hydrogène). Dans le cas des liaisons doubles,
les deux cylindres de modélisation seront écartés de 0.1.
Solutions
| Quatre cubes (Question 3) |
| Trois cubes |
| Bras robot avec parallélépipèdes |
| Bras robot avec cylindres |
| Molécule de benzène |
![]()
TD n°2 : Modélisation par facettes
Exercice n°1
a) Modéliser par facettes un cube de coté c centré sur l'origine du repère de modélisation. On ne générera
pas les normales.
La fonction créée aura pour prototype:
void mySolidCube(double c);
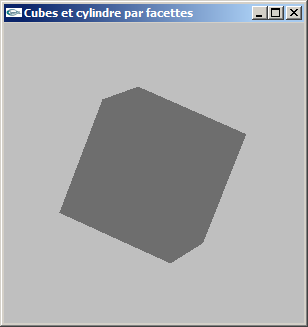
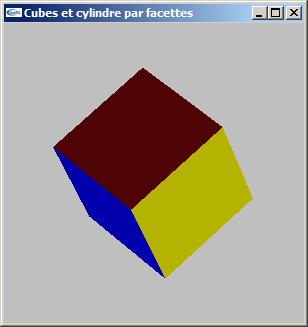
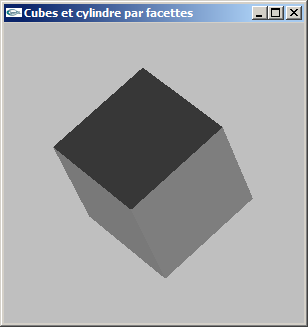
b) Modifier la modélisation de la question précédente pour ajouter la gestion des normales.
Le but est de rendre possible les calculs d'éclairage.
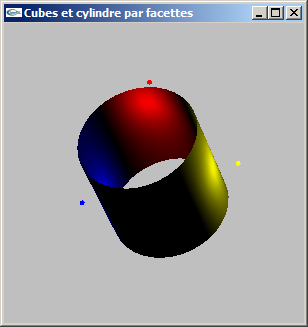
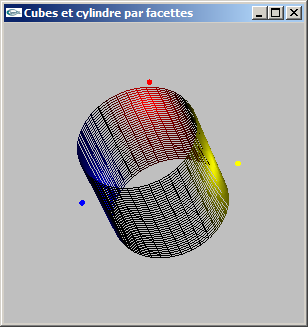
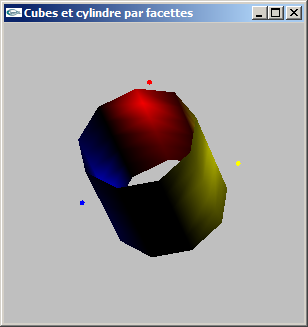
a) Modéliser par facettes un cylindre selon les caractéristiques suivantes:
- choix du rayon,
- choix de la hauteur,
- choix du nombre de facettes en découpage longitudinal pour une valeur entière ns,
- centré sur l'origine du repère de modélisation,
- axé selon y.
On ne modélisera pas les bases du cylindre, mais uniquement le tube.
La fonction créée aura pour prototype:
void mySolidCylinder(double hauteur, double rayon, int ns);
b) Ajouter un découpage latéral (selon l'axe y) pour une valeur nl.
Le prototype de la fonction devient:
void mySolidCylindre(double hauteur, double rayon, int ns, int nl);
Solutions
![]()
TP n°1 : Premières implantations OpenGL
Exercice n°1
Télécharger le fichier archive 2015-2016.zip. Ce fichier archive contient une "solution" Visual Studio 2010.
Après extraction, un répertoire IG-2015-2016 est créé qui contient lui-même 5 répertoires:
- Bin pour les exécutables,
- Include pour les fichiers d'entête OpenGL (fichiers non présents dans Visual Studio),
- Lib pour les fichiers librairie OpenGL (fichiers non présents dans Visual Studio),
- Projet pour le fichier de description de la solution (Projet.sln) et les répertoires contenant les projets faisant partie de la solution
(Un seul répertoire actuellement: Exemple),
- Src pour les fichiers source des projets inclus dans la solution.
La solution comprend un seul projet nommé Exemple. Ce projet inclut un seul fichier source Exemple.cpp et est configuré pour une compilation utilisant
OpenGL:
- fichiers d'entête (répertoire implicite ../../Include),
- fichiers librairie (fichiers OpenGL32.ms.lib, glu32.ms.lib, glut32.ms.lib),
- copie de l'exécutable dans le répertoire Bin.
La compilation (génération) de ce projet doit conduire à la création d'un exécutable nommé Exemple.exe dans le répertoire Bin. Son exécution
requière les dll OpenGL32.dll et Glu32.dll (toujours présentes dans le système d'exploitation Windows) ainsi que la librairie Glut32.dll (jamais
présente dans le système d'exploitation Windows mais dont il existe une copie dans le répertoire Bin).
a) Extraire l'archive IG-2015-2016. Lancer Visual Studio 2010 et charger la solution. Vérifier la compilation et l'exécution du projet Exemple.
Les cylindres n'existent pas dans GLUt, on pourra utiliser le module suivant pour les modéliser: ModuleCylindres.h, ModuleCylindres.cpp.
b) Implanter la question (4) de l'exercice n°1 du TD n°1.
c) Implanter l'exercice n°3 du TD n°1.
TD n°3 : Paramètrage numérique de caméras
Exercice n°1
a) On considère une caméra de visualisation en projection parallèle orthographique placée en position (0.0, 0.0, 0.0) orientée selon l'axe (0.0,
0.0, -1.0). On considère une scène centrée sur le point de coordonnées (0.0, 0.0, -100.0) et occupant un volume circulaire de rayon voisin de 10.0.
Quelle ouverture doit-on donner à cette caméra pour visualiser cette scène en gros plan dans la fenêtre d'affichage?
b) On considère une caméra de visualisation en projection en perspective placée en position (0.0, 0.0, 0.0) orientée selon l'axe (0.0, 0.0, -1.0).
On considère une scène centrée sur le point de coordonnées (0.0, 0.0, -100.0) et occupant un volume circulaire de rayon voisin de 10.0.
Quelle ouverture doit-on donner à cette caméra pour visualiser cette scène en gros plan dans la fenêtre d'affichage?
Exercice n°2
Une caméra de visualisation en perspective OpenGL est obligatoirement placée en position (0.0, 0.0, 0.0) du repère de modélisation. Elle est obligatoirement orientée selon l'axe de projection (0.0, 0.0,-1.0).
a) On considère une scène modélisée au sein d'une fonction C de manière à être centrée autour de l'origine du repère de modélisation associé
à la fonction.
Quelle(s) transformation(s) géométrique(s) de modification du repère courant (placée(s) entre la configuration de projection de la caméra et la modélisation
effective) doit on réaliser pour que cette scène soit vue centrée dans la fenêtre de visualisation comme placée devant la caméra à une distance de
100.0 avec un axe de projection selon la direction (0.0, 0.0, -1.0) dans le repère de modélisation de la scène?
A quelle position de placement de la caméra cela correspond-t-il dans le repère de modélisation de la scène?
b) On considère la scène de la question (a).
Quelle(s) transformation(s) géométrique(s) de modification du repère courant (placée(s) entre la configuration de projection de la caméra et la modélisation
effective) doit on réaliser pour que cette scène soit vue centrée dans la fenêtre de visualisation comme placée devant la caméra à une distance de
100.0 avec un axe de visualisation selon la direction (-1.0, 0.0, -1.0) dans le repère de modélisation?
A quelle position de placement de la caméra cela correspond-t-il dans le repère de modélisation de la scène?
c) On considère la scène de la question (a).
Quelle(s) transformation(s) géométrique(s) de modification du repère courant (placée(s) entre la configuration de projection de la caméra et la modélisation
effective) doit on réaliser pour que cette scène soit vue centrée dans la fenêtre de visualisation comme placée devant la caméra à une distance de
100.0 avec un axe de visualisation selon la direction (-1.0, -1.0, -1.0) dans le repère de modélisation?
A quelle position de placement de la caméra cela correspond-t-il dans le repère de modélisation de la scène?
Solutions
TP n°2 : Scènes OpenGL, GLUT et caméras
Exercice n°1
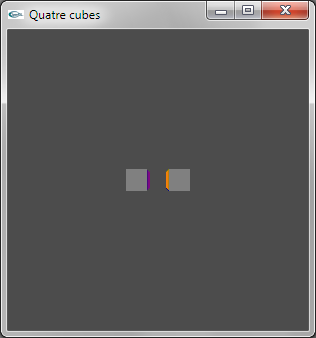
Implanter et tester le fonctionnement de l'exercice n°1 du TD n°1 (quatre cubes).
- Travailler sur une copie du fichier source Exemple.cpp.
- Mettre en commentaire la ligne glutIdleFunc de la fonction main.
- Modifier la fonction keyboard pour que l'animation soit inactivée au lancement mais reste activable (animation d'une scène immobile! -> Réaffichage en boucle de la même image).
- Réécrire la fonction void scene(void) avec celle du TD. On utilisera la fonction void glutSolidCube(double c) de la librairie GLUt comme fonction de modélisation de cube.
- Adapter la fonction idle pour que la scène tourne sur elle-même.
Exercice n°2
Tester les trois possibilités existant pour ajuster la taille des objets à l'écran de manière à voir la scène en gros plan:
- Jouer sur l'angle d'ouverture de la caméra virtuelle.
- Jouer sur la distance entre la scène et la caméra virtuelle.
- Jouer sur la taille de la scène

Exercice n°3
a) Ajouter un contrôle clavier pour que les cubes de la scène puissent être remplacés par des sphères (et réciproque). La fonction void glutSolidSphere(double rayon, int n,int m) peut être utilisée pour modéliser une sphère.
b) Ajouter un contrôle clavier pour que les objets puissent être affichés soit en mode plein, soit en mode fil de fer (fonction glPolygonMode d'OpenGL).
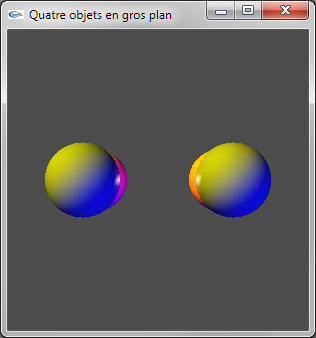
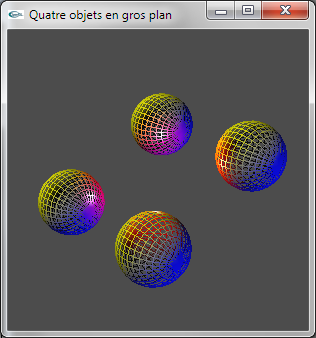
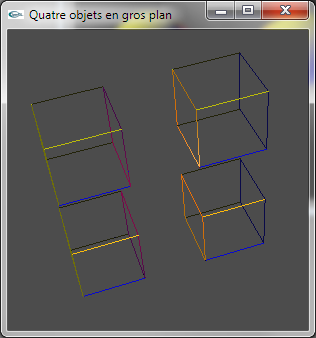
Exercice n°4
a) Tester les configurations de caméra définies aux 3 questions de l'exercice n°2 du TD n°3.
b) Tester la configuration par gluLookAt d'une caméra placée en position (0.0, 100.0, 0.0), orientée vers l'origine et d'axe vertical (0.0, 1.0, 0.0).
Solutions
TD n°4 : Lumières et matériaux en OpenGL
Exercice n°1
a) Développer le code source OpenGL permettant de configuer la lumière n°0 en tant que lumière ponctuelle placée en position (0.0, 0.0, 2.5). Sa composante d'émission diffuse est rouge. Sa composante d'émission spéculaire est blanche.

b) Développer le code source OpenGL permettant de configuer la lumière n°1 en tant que lumière directionnelle de direction d'incidence (1.0, 0.0, 0.0). Sa composante d'émission diffuse est verte. Sa composante d'émission spéculaire est blanche.
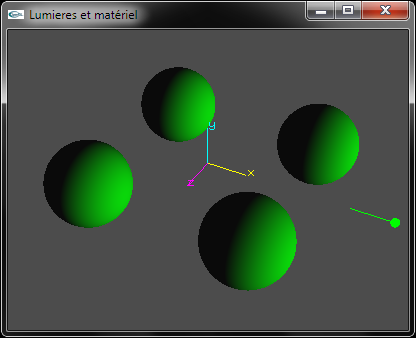
c) Développer le code source OpenGL permettant de configuer la lumière n°2 en tant que spot placé en position (2.0, 10.0, 2.0), orienté vers le point de coordonnées (-2.0, 0.0, -2.0) et d'ouverture 20.0°. Sa composante d'émission diffuse est bleue. Sa composante d'émission spéculaire est blanche.
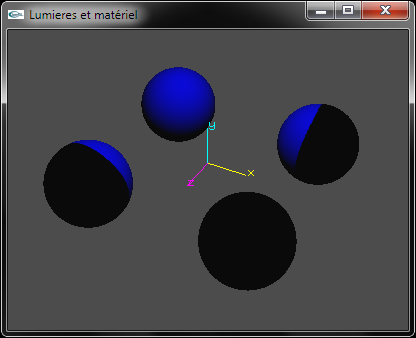 Spot bleu uniquement |
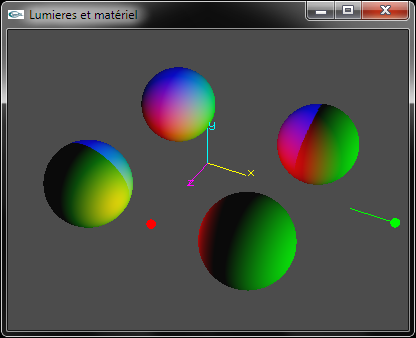 Addition des 3 lumières |
d) Ajouter au code de paramétrage la lumière n°0 les appels OpenGL permettant de configurer une atténuation de l'éclairage en fonction inversement proportionnelle du carré de la distance entre la source lumineuse et le point éclairé.
 Pas d'atténuation |
 Atténuation quadratique |
e) Proposer une solution permettant de choisir la position de placement de la lumière ponctuelle de la question (a) et la direction d'orientation de la lumière directionnelle de la question (b) par rotation d'une valeur d'angle autour de l'axe Oy.
 Lumières en position initiale |
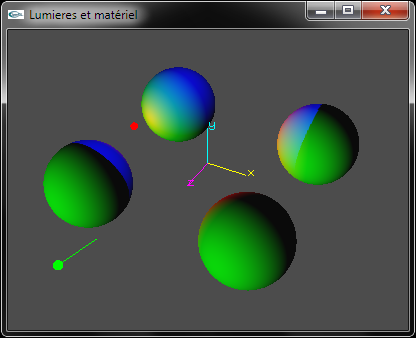 Rotation des lumières |
Exercice n°2
a) Développer le code source OpenGL permettant de configurer le matériel pour qu'il adopte la couleur blanche en diffusion et la couleur noire en spéculaire, ambiant et émission.
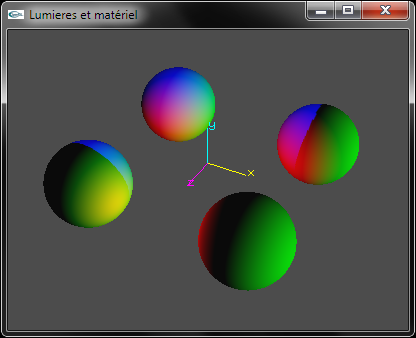 Sans réaffectation des valeurs par défaut du matériel |
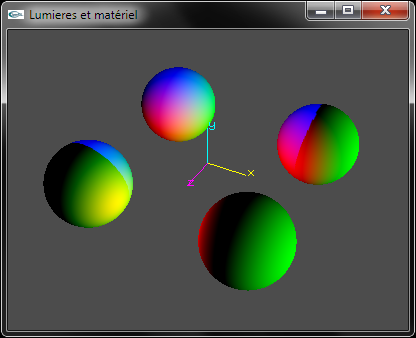 Avec réaffectation des valeurs par défaut du matériel |
b) Développer le code source OpenGL permettant de configurer le matériel pour qu'il adopte la couleur rouge en diffusion et la couleur noire en spéculaire, ambiant et émission.

c) Développer le code source OpenGL permettant de configurer le matériel pour qu'il adopte la couleur jaune en diffusion et la couleur noire en spéculaire, ambiant et émission.

d) Développer le code source OpenGL permettant de configurer le matériel pour qu'il adopte la couleur blanche en diffusion et spéculaire et la couleur noire en ambiant et émission. La réflectivité est configurée avec la valeur 64.0.
Solution
|
GLUT |
||
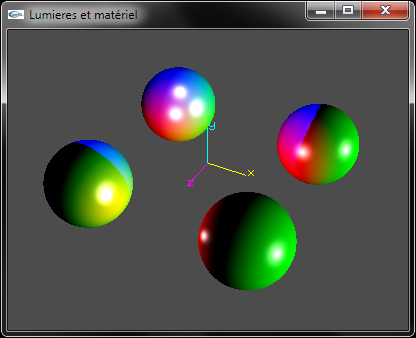
| Lumières et matériel | ||
![]()
TP n°3 : Lumières et matériaux en OpenGL
Implanter les exercice du TD n°4 sur la scène du TP n°2 constituée de 4 sphères.
Solution
|
GLUT |
||
| Lumières et matériel | ||
![]()
TD n°5 : Mathématiques de l'Informatique Graphique
Exercice n°1
Proposer une méthode permettant de tester la planarité d'une facette à 4 sommets.
Exercice n°2
a) Développer en C++ une classe CoordonneesHomogenes3D.
b) Dériver de la classe CoordonneesHomogenes3D une classe Position3D pour le stockage de positions dans un espace à trois dimensions.
c) Dériver de la classe CoordonneesHomogenes3D une classe Direction3D pour le stockage de directions dans un espace à trois dimensions.
d) Développer une méthode de calcul du produit scalaire de deux Direction3D.
e) Développer une méthode de calcul du produit vectoriel de deux Direction3D.
f) Implanter une fonction ou une méthode de test de la planarité de facettes à 4 sommets.

Solutions
![]()
TP n°4 : Animation en OpenGL et GLUt
Le but du TP consiste à implanter une animation où une sphère de 20 pixels de rayon se déplace dans une fenêtre de 600x400 pixels et rebondit sur
ses bords horizontaux et verticaux.
Les paramètres d'animation sont les suivants:
- La sphére se déplace à raison de 1 pixel de déplacement horizontal et de 1 pixel de déplacement vertical entre chaque image (déplacements
unitaires à valeurs positives ou négatives).
- Lorsqu'un bord est touché, le sens de déplacement horizontal (resp. vertical) est négativé s'il s'agit d'un bord vertical
(resp. horizontal).
Quelques indications:
- Le mode de projection en perspective est inadapté à ce TP car la position réelle et la position écran de la sphère doivent être parfaitement
contrôlées, ce que ne permet pas la perspective. On travaillera donc en projection parallèle orthographique.
- Les déplacements étant comptés en pixels, il est préférable d'adopter un repère virtuel de visualisation qui permet de compter les distances
directement en pixels dans le cadre du repère de modélisation.
Solution
![]()
TD n°6 : Mathématiques de l'Informatique Graphique
Exercice n°1
a) Développer en C++ une classe TransformationGeometrique3D en coordonnées homogènes.
b) Dériver de la classe TransformationGeometrique3D une classe Translation3D pour le stockage d'opérateurs de type translation de vecteur (tx, ty, tz).
c) Dériver de la classe TransformationGeometrique3D une classe Rotation3D pour le stockage d'opérateurs de type rotation d'angle a autour de l'axe (ax, ay, az) passant par l'origine.
d) Implanter une méthode de transformation d'une position ou d'une direction par une translation ou une rotation.
e) Implanter une méthode de composition d'une transformation géométrique par une transformation géométrique.
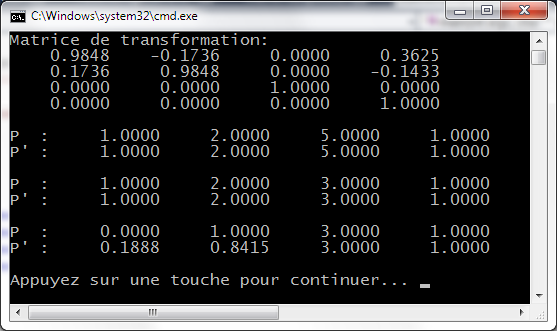
Solutions
![]()
TP n°5 : Coordonnées homogènes et transformations géométriques
Le fichier code source RotationCube_TP.cpp implante un programme de modélisation, d'affichage et d'animation d'un cube en fil de fer. La modélisation du cube est réalisée au moyen d'une primitive graphique OpenGL de type GL_LINES. L'animation est obtenue par la réalisation de deux rotations successives d'angles r1 et r2 avec incrémentation de r1 et r2 entre chaque image. Le code correspondant est à trouver dans la fonction void scene1(void).
a) Télécharger, compiler et exécuter ce fichier source.
On souhaite ne plus utiliser la fonction glRotatef d'OpenGL. La seule solution à notre disposition consiste à implanter les opérations mathématiques nécessaires à la réalisation de rotations. Le fichier archive MathematiquesIG_TP.zip contient les classes CoordonneesHomogenes3D, Position3D et Direction3D de gestion des coordonnées homogènes ainsi que les classes TransformationGeometrique3D, Translation3D, Rotation3D et Scale3D de gestion de transformations géométriques en coordonnées homogènes.
b) Télécharger et compiler les fichiers de cette archive en les intégrant au projet de la question (a).
c) Ecrire (remplir) les fonctions compose et transforme de la classe TransformationGeometrique3D.
d) Reprendre le code source RotationCube_TP.cpp pour écrire (remplir) la fonction void scene2(void) pour qu'elle réalise les mêmes opérations que la fonction void scene1(void) mais sans utiliser glRotatef. La touche Enter utilisée en cours d'exécution permet de switcher entre scene1 et scene2.
Solutions
![]()
TP n°6 : Plaçage de texture
L'archive zip suivante contient les fichiers sources d'une librairie de gestion des fichiers png: Png.zip.
Plus précisément, les deux fonctions d'importation et d'exportation sont décrites dans le fichier
ChargePngFile.h.
La fonction d'importation prend en paramètre le nom du fichier à importer et deux pointeurs sur entier destinés à récupérer la résolution en
x et la résolution en y de l'image importée. Elle retourne un pointeur sur unsigned char correspondant au tableau d'octets issu de l'importation
(NULL si échec). Le tableau retourné est alloué dynamiquement par malloc et se doit d'être libéré par free après utilisation. Il contient les
composantes RVB des pixels codées sur 8 bits et entrelacées.
a) Importer cette archive, en faire l'extraction, inclure l'ensemble des fichiers qu'elle contient dans un projet de développement, vérifier la compilation et l'exécution par importation d'une image png sous la forme d'un tableau de pixels (sans affichage). On pourra se servir de l'image Test.png qui est formée d'une matrice de 64x64 pixels dont la première ligne est bleue.
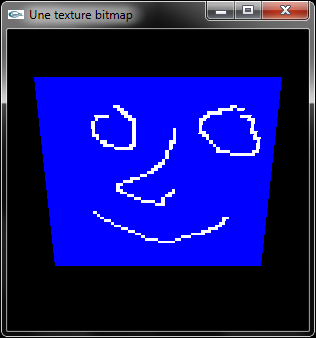
b) Implanter un programme OpenGL de dessin d'un carré de coté 6.0 sur lequel est placée une image bitmap.

c) Implanter un programme OpenGL de modélisation d'un cylindre sur le tube duquel est placée une texture bitmap.
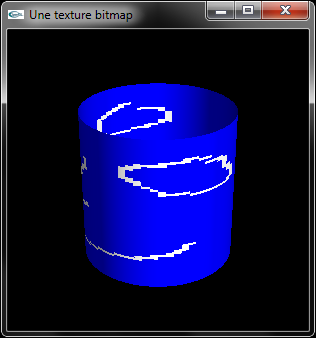

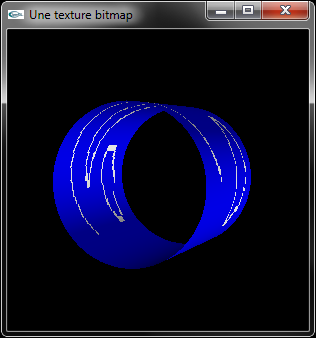
On pourra utiliser et adapter la fonction ci-dessous.
/* Modelisation par facettes d'un cylindre */
#ifndef M_PI
#define M_PI 3.14159265358979
#endif
static void myCylindre(double hauteur,double rayon,int ns) {
glPushMatrix();
hauteur /= 2.0F;
glBegin(GL_QUAD_STRIP);
for( int i = 0 ; i <= ns ; i++ ){
double a = (2.0*M_PI*i)/ns;
float cs = cos(a);
float sn = -sin(a);
glNormal3f(cs,0.0F,sn);
float x = rayon*cs;
float z = rayon*sn;
glVertex3f(x,hauteur,z);
glVertex3f(x,-hauteur,z); }
glEnd();
glPopMatrix();
}
On pourra se reporter au chapitre sur le texturage pour une description plus précise des principes utilisés pour cette technique et à la partie 3 du chapitre sur OpenGL pour son application en OpenGL.
Solution
![]()
TD n°7 : Tracé de courbes B-Splines
On souhaite implanter le calcul de courbes lissées de type B-Spline.
Exercice n°1
Développer une classe permettant de modéliser une ligne polygonale 3D.
A terme, cette classe permettra de modéliser:
- les lignes polygonales devant être lissées,
- les lignes polygonales obtenues par lissage.
Exercice n°2
Les classes développées dans les TD-TP précédents pour modéliser des vecteurs à 4 composantes et des matrices à 4x4 composantes comportent des méthodes de calcul de produits matriciels qui nous seraient utiles pour l'implantation du calcul de courbes B-Splines. Or, il n'est pas souhaitable d'utiliser les classes déjà créées à cette fin car elles seraient détournées de leur usage normal. Un travail de redesign est nécessaire (voir hiérarchie de classes en bas de cette page web).
a) Reprendre la classe mère CoordonneesHomegenes3D pour la faire dériver d'une classe mère Vecteur4.
b) Reprendre la classe mère TransformationGeometrique3D pour la faire dériver d'une classe mère Matrice4x4. Déplacer dans cette classe les opérateurs de réalisation du produit matrice-vecteur et du produit matrice-matrice.
c) Faire dériver de la classe Matrice4x4 une classe MatriceDeBase qui sera spécifiquement utilisée pour la modélisation des matrices de base utilisées pour le lissage des courbes B-Splines.
d) Implanter un constructeur de calcul d'une ligne polygonale par lissage d'un quadruplet de sommets 3D au moyen d'une courbe B-Spline. Outre les sommets de contrôle, les paramètres seront la matrice de base et le nombre de sommets.
f) Implanter un constructeur de calcul d'une ligne polygonale par lissage d'une ligne polygonale au moyen d'une courbe B-Spline par morceaux. Outre les sommets de contrôle, les paramètres seront la matrice de base et le nombre de sommets.
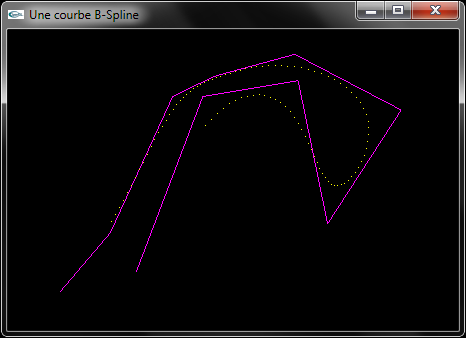
Solutions
![]()
TP n°7 : Clipping par l'algorithme de Cohen-Sutherland
On considère les fichiers sources contenus dans le fichier zip suivant: ClippingCohenSutherlandVide.zip.
Ils constituent une application OpenGL de calcul et d'affichage d'un segment clippé dans un rectangle à bord horizontaux et verticaux au
moyen de l'algorithme de Cohen-Sutherland. Les méthodes correspondant aux questions (a), (b), (c) et (d) suivantes ont été "vidées".
Il convient de les complèter pour que l'application devienne compilable et exécutable.
On précise que les deux classes importantes sont les classes Segment2D et Rectangle2D. La classe Segment2D possède 2 Position2D pour attributs: Les
extrémités du segment. La classe Rectangle2D possède elle aussi 2 Position2D pour attributs: Les coins supérieur gauche (x et y minimum du rectangle)
et inférieur droit (x et y maximum du rectangle).
a) Développer une méthode permettant de déterminer le code de Cohen-Sutherland (valeur entière) d'une Position2D vis à vis d'un Rectangle2D.
b) Développer une méthode permettant de déterminer l'abscisse de l'intersection entre un Segment2D et une droite horizontale (connue par son ordonnée).
c) Développer une méthode permettant de déterminer l'ordonnée de l'intersection entre un Segment2D et une droite verticale (connue par son abscisse).
d) Développer une méthode permettant de clipper un Segment2D dans un Rectangle2D (algorithme de Cohen-Sutherland).
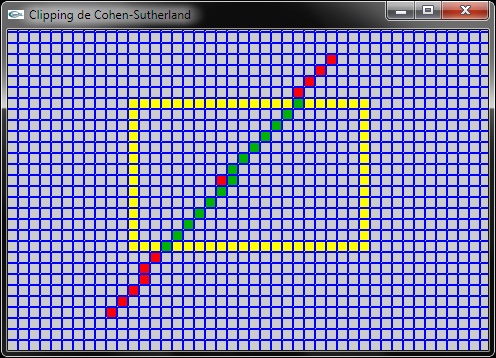
Solutions
![]()
TD n°8 : Remplissage d'une facette triangulaire
Implanter une fonction de remplissage 2D d'un triangle.

Méthode: Remplir un triangle en 2D peut être réalisé en traçant toutes les lignes horizontales de pixels délimitées par ses bords gauche et droit. Il convient donc de déterminer les abscisses extrèmes de ces lignes horizontales pour chacun des y compris entre ymin et ymax où ymin (resp. ymax) est la valeur minimale (resp. maximale) des ordonnées des 3 sommets de définition du rectangle.
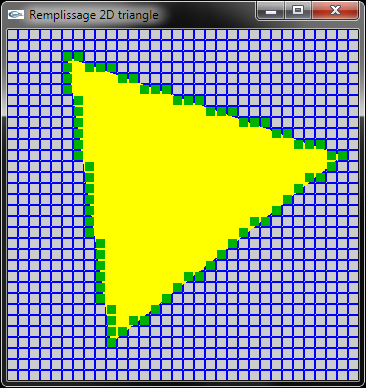
Ainsi, deux tableaux xd et xg sont calculés dont les indices correspondent aux ordonnées y des lignes de pixels.
Le calcul de ces deux tableaux est réalisé par implantation et adaptation de l'algorithme de Bresenham pour le tracé de segments de droite. Cet
algorithme adapté est appliqué aux trois bords du triangle rempli.


Solutions
![]()
TP n°8 : Calcul de la quantité d'énergie diffusée en un point éclairé par une source lumineuse
On considère les classes Rvb, Couleur, Energie suivantes:
- Rvb.h
- Rvb.cpp
- Couleur.h
- Couleur.cpp
- Energie.h
- Energie.cpp
La classe mère Rvb permet le stockage d'une information rvb à composantes réelles.
La classe Couleur dérive de Rvb et est utilisée pour coder des couleurs rvb ou des coefficients rvb colorés (composantes comprises entre 0.0 et 1.0).
La classe Energie dérive de Rvb et est utilisée pour coder une énergie colorée (composantes comprises entre 0.0 et +µ).
On considère les classes Lumiere et LumiereDirectionnelle suivantes:
- Lumiere.h
- Lumiere.cpp
- LumiereDirectionnelle.h
- LumiereDirectionnelle.cpp
La classe mère Lumiere permet le stockage d'une lumière par la définition de ses attributs de couleur, d'intensité d'émission et d'activation/désactivation.
Elle n'est pas destinée à être instanciée.
La classe LumiereDirectionnelle dérive de Lumiere et implante une lumière directionnelle par la définition d'un attribut supplémentaire donnant
la direction d'émission de la lumière.
a) Développer une méthode permettant de calculer la quantité d'énergie diffusée sous l'éclairage d'une LumiereDirectionnelle en une Position3D extraite d'une surface où la normale est connue sous la forme d'une Direction3D. Les coefficients de diffusion de la surface sont définis par la donnée d'une Couleur. La formule de calcul à utiliser est la formule de Lambert.

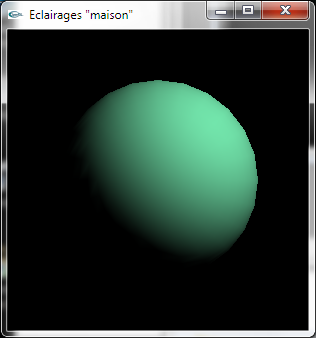

Sphère éclairée par une lumière directionnelle
en pur OpenGL à gauche, en utilisant le calcul de diffusion "maison"
Pour cette question, il convient de développer une méthode virtuelle dans la classe Lumiere qui sera implantée concrètement dans la classe LumiereDirectionnelle.
Son prototype est:
virtual void energieDiffusee(Energie *e,Position3D *p,Direction3D *n,Couleur *kd)
où e est l'énergie diffusée (à calculer), p la position du point de diffusion, n la normale au point p et kd le coefficient de diffusion au point
p.
Remarque: Pour le calcul de diffusion de Lambert sous une lumière directionnelle, la position p n'est pas utilisée. Elle apparaît dans le prototype
pour compatibilité de la méthode virtuelle avec d'autres types de lumières.
On considère la classe LumierePonctuelle suivante:
- LumierePonctuelle.h
- LumierePonctuelle.cpp
La classe LumierePonctuelle dérive de Lumiere et implante une lumière ponctuelle par la définition d'un attribut supplémentaire donnant la position
de la lumière.
b) Développer une méthode permettant de calculer la quantité d'énergie diffusée sous l'éclairage d'une LumierePonctuelle en une Position3D extraite d'une surface où la normale est connue sous la forme d'une Direction3D. Les coefficients de diffusion de la surface sont définis par la donnée d'une Couleur.
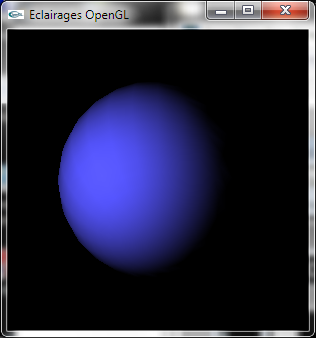
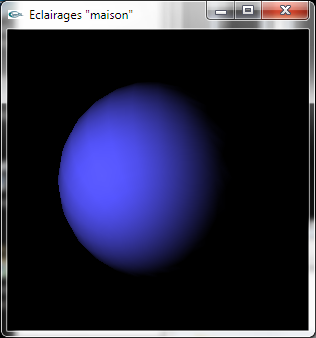

Sphère éclairée par une lumière ponctuelle
en pur OpenGL à gauche, en utilisant le calcul de diffusion "maison"
Pour cette question, il convient de développer une nouvelle implantation de la méthode de calcul de diffusion dans la classe LumierePonctuelle.
On pourra utiliser le programme DiffusionsLambertiennes.cpp et les classes mathématiques
MathematiquesIG.zip pour tester les deux méthodes développées.
Ce programme affiche deux fenêtres avec, dans la première, une sphère éclairée au moyen de l'implantation OpenGL du calcul de diffusion de Lambert
et dans la seconde, une sphère éclairée au moyen de l'implantation réalisée.
Remarque: Ce code source montre comment utiliser deux (plusieurs par extension) fenêtres ainsi que les menus popup.
Solutions
![]()
TP n°9 : Lancer de rayons: Calcul des directions de réflexion et transmission
a) Concevoir une méthode de la classe Direction3D permettant de calculer la direction d'un rayon réfléchi lors d'une réflexion spéculaire.
Son prototype sera:
int reflexion(Direction3D *i,Direction3D *n);
La méthode retourne 1 et affecte this avec la direction de réflexion correspondant à la direction incidente normée i et à la normale (normée) n.
S'il n'y a pas de réflexion, 0 est retourné et this est inchangé.
b) Concevoir une méthode de la classe Direction3D permettant de calculer la direction d'un rayon transmis à l'interface entre deux milieux
lors du passage entre ces deux milieux.
Son prototype sera:
int transmission(Direction3D *i,Direction3D *n,double niSurNt);
La méthode retourne 1 et affecte this avec la direction de transmission correspondant à la direction incidente normée i, à la normale
(normée) n et au rapport niSurNt entre les indices de réfraction des milieux incident et de transmission. S'il n'y a pas de transmission,
0 est retourné et this est inchangé.

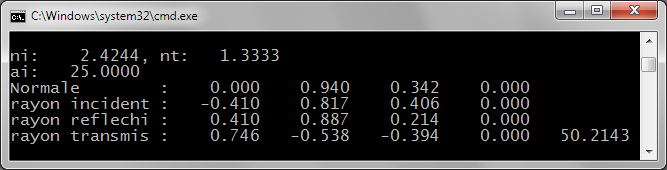
Fig 1: Rayon incident en jaune, normale en magenta, rayon réfléchi en rouge, rayon transmis en bleu
ni > nt -> Rayon transmis dévié vers le plan d'interface
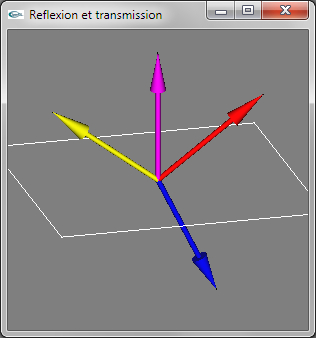
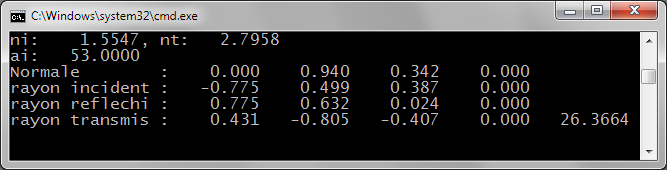
Fig 2: ni < nt -> Rayon transmis dévié vers le vecteur opposé au vecteur normal
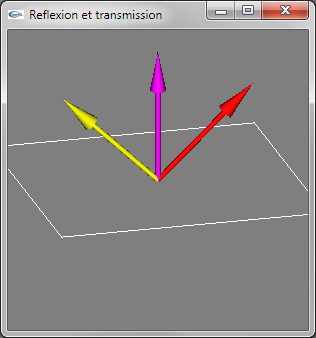

Fig 3: Cas particulier: Pas de rayon transmis
On pourra utiliser le programme RayTracingVide.zip (fonction main dans RayTracing.cpp) pour tester les 2 méthodes développées. Ce programme implante un calcul d'images par lancer de rayons.
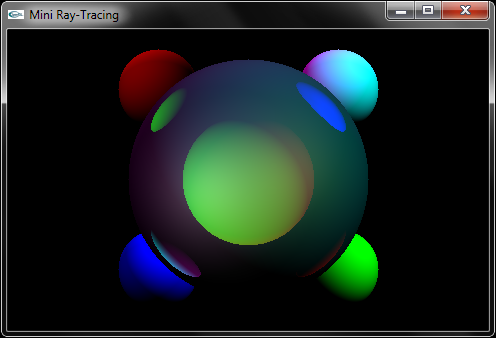
Il s'appuie sur l'ensemble des classes développées depuis le début des séances de TD et de TP (voir ci-dessous).
Attention: Dans le fichier RayTracingVide.zip, le fichier ReflexionEtTransmission.cpp contient aussi une fonction main. Il convient
de ne pas l'inclure dans la liste des fichiers à compiler pour générer l'application de lancer de rayon. Ce fichier permet de créer l'application
qui a été utilisée pour générer les copies d'écran des figures 1, 2 et 3.
Solutions
![]()
TP n°10 : Transformations géométriques pour la visualisation
a) On donne les lignes de code suivantes:
static const int nbP = 30;
static float smmts[nbP][4] =
{ { -20.0F, 0.0F, 15.0F, 1.0F },{ 20.0F, 0.0F, 15.0F, 1.0F },
{ 20.0F, 20.0F, 15.0F, 1.0F },{ -20.0F, 20.0F, 15.0F, 1.0F },
{ -20.0F, 0.0F,-15.0F, 1.0F },{ 20.0F, 0.0F,-15.0F, 1.0F },
{ 20.0F, 20.0F,-15.0F, 1.0F },{ -20.0F, 20.0F,-15.0F, 1.0F },
{ 20.0F, 30.0F, 0.0F, 1.0F },{ -20.0F, 30.0F, 0.0F, 1.0F },
{ 20.0F, 0.0F, 4.0F, 1.0F },{ 20.0F, 15.0F, 4.0F, 1.0F },
{ 20.0F, 15.0F, -4.0F, 1.0F },{ 20.0F, 0.0F, -4.0F, 1.0F },
{ 5.0F, 7.0F, 15.0F, 1.0F },{ -5.0F, 7.0F, 15.0F, 1.0F },
{ -5.0F, 15.0F, 15.0F, 1.0F },{ 5.0F, 15.0F, 15.0F, 1.0F },
{ 15.0F, 7.0F,-15.0F, 1.0F },{ 5.0F, 7.0F,-15.0F, 1.0F },
{ 5.0F, 15.0F,-15.0F, 1.0F },{ 15.0F, 15.0F,-15.0F, 1.0F },
{ -5.0F, 7.0F,-15.0F, 1.0F },{ -15.0F, 7.0F,-15.0F, 1.0F },
{ -15.0F, 15.0F,-15.0F, 1.0F },{ -5.0F, 15.0F,-15.0F, 1.0F },
{ -20.0F, 7.0F, 5.0F, 1.0F },{ -20.0F, 15.0F, 5.0F, 1.0F },
{ -20.0F, 15.0F, -5.0F, 1.0F },{ -20.0F, 7.0F, -5.0F, 1.0F } };
static const int nbS = 34;
static int sgmts[nbS][2] =
{ { 0, 1 },{ 1, 2 },{ 2, 3 },{ 3, 0 },{ 4, 5 },
{ 5, 6 },{ 6, 7 },{ 7, 4 },{ 0, 4 },{ 1, 5 },
{ 8, 9 },{ 8, 6 },{ 9, 3 },{ 8, 2 },{ 9, 7 },
{ 10,11 },{ 11,12 },{ 12,13 },{ 14,15 },{ 15,16 },
{ 16,17 },{ 17,14 },{ 18,19 },{ 19,20 },{ 20,21 },
{ 21,18 },{ 22,23 },{ 23,24 },{ 24,25 },{ 25,22 },
{ 27,26 },{ 28,27 },{ 29,28 },{ 26,29 } };
Ces lignes réalisent la déclaration dans le tableau smmts de nbP = 30 sommets en trois dimensions et la déclaration dans le tableau sgmts de nbS = 34 segments de droite par la donnée de 34 couples d'indices de sommet du tableau smmts.
Utiliser ces données pour afficher en fil de fer l'objet ainsi modélisé.
b) Le but de la suite du TP est d'implanter les transformations géométriques de visualisation telles que réalisées au sein d'OpenGL.
On connait les coordonnées des objets modélisés dans le repère global (coordonnées ci-dessus).
On connait la position Po =  de l'observateur dans le repère global.
de l'observateur dans le repère global.
On connait la position Pv =  d'un point directement "regardé" par l'observateur.
d'un point directement "regardé" par l'observateur.
On souhaite transformer du repère global vers le repère observateur les coordonnées des objets modélisés.
Ce repère possède les 3 caractéristiques suivantes:
- Après transformation, l'observateur est placé à l'origine.
- Après transformation, le point Pv est placé sur l'axe -Oz.
- Après transformation, l'axe y (0.0,1.0,0.0) du repère global projeté en 2D par suppression de z apparaît vertical c'est à dire que
sa coordonnée x est forcément égale à 0.0. Cette caractéristique est implantée de manière que tout ce qui est vertical dans le repère global reste
apparemment vertical dans le repère observateur.
Remarque: On réalise ici une transformation voisine du gluLookAt de glu.
La matrice de transformation utilisée est: 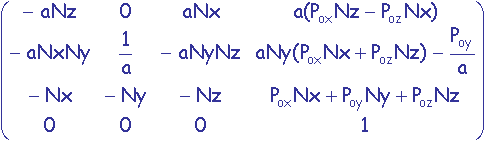
dans laquelle on retrouve les coordonnées de Po
mais aussi les coordonnées  du vecteur normé de Po vers Pv (coordonnées calculables)
du vecteur normé de Po vers Pv (coordonnées calculables)
et la valeur a = 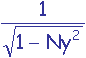 (valeur calculable).
(valeur calculable).
Dériver de la classe TransformationGeometrique3D une classe LookAt implantant la transformation géométrique ci-dessus.
Utiliser cette classe pour réaliser la transformée des positions définies dans le tableau smmts. On choisira Po = (200.0,60.0,120.0) et Pv = (0.0,0.0,0.0).
Utiliser les coordonnées obtenues pour afficher l'objet modélisé en implantant une visualisation en projection parallèle orthographique. Pour
ce faire, on utilisera uniquement les coordonnées x et y, z étant considéré avoir pour valeur 0.0.
Remarque: L'affichage étant réalisé en OpenGL, il est impossible de ne pas utiliser de fonction reshape. En conséquence, on utilisera la fonction
suivante: suivante:
void reshape(int x,int y) {
glViewport(0,0,x,y);
glMatrixMode(GL_PROJECTION);
glLoadIdentity();
glOrtho(-x/2.0,-x/2.0+x,-y/2.0,-y/2.0+y,-10.0,10.0);
glMatrixMode(GL_MODELVIEW);
glLoadIdentity();
}
Cette fonction implante une visualisation telle que l'origine est placée au centre de la fenêtre de visualisation et les coordonnées comptent
des pixels.
c) On souhaite visualiser la scène en utilisant une projection en perspective plutôt qu'une projection parallèle orthographique.
Implanter une visualisation en perspective est réalisé en transformant chaque sommet (obtenu après la transformation géométrique repère global -> repère observateur) par division de sa coordonnée x (resp. y) par sa distance en z pour obtenir sa coordonnée écran x' (resp. y') puis en utilisant (x',y') comme coordonnées d'affichage.
d) On souhaite maintenant réaliser une animation de caméra consistant à déplacer la position de l'observateur sans changer le point qu'il
regarde.
Une courbe 3D lissée va être utilisée pour définir les positions successives qu'il adopte. Les sommets suivants sont les points de contrôle à
utiliser pour définir cette courbe dans le cadre de la génération d'une B-Spline non rationnelle uniforme.
static const int nbT = 18;
static float ptT[nbT][4] =
{ { 200.0F, 60.0F, 120.0F, 1.0F },{ 200.0F, 60.0F, 120.0F, 1.0F },
{ 200.0F, 60.0F, 120.0F, 1.0F },{ 170.0F, 100.0F, 120.0F, 1.0F },
{ 120.0F, 90.0F, 200.0F, 1.0F },{ 120.0F, 60.0F, 200.0F, 1.0F },
{ -100.0F, 90.0F, 200.0F, 1.0F },{ -150.0F, 130.0F, 150.0F, 1.0F },
{ -200.0F, 180.0F, 0.0F, 1.0F },{ -180.0F, 230.0F, -150.0F, 1.0F },
{ -150.0F, 0.0F, -160.0F, 1.0F },{ 0.0F, 0.0F, -200.0F, 1.0F },
{ 50.0F, 30.0F, -180.0F, 1.0F },{ 150.0F, 60.0F, 60.0F, 1.0F },
{ 200.0F, 60.0F, 120.0F, 1.0F },{ 0.0F, 0.0F, 0.0F, 1.0F },
{ 0.0F, 0.0F, 0.0F, 1.0F },{ 0.0F, 0.0F,
0.0F, 1.0F } };
Pour générer cette courbe lissée, on pourra utiliser la classe LignePolygonale qui permet de modéliser des lignes brisées et de les lisser et la
classe MatriceDeBase qui décrit des matrices de base utilisables pour créer des B-Splines.
Ces classes sont définies au sein des fichiers suivants:
- LignePolygonale.h
- LignePolygonale.cpp
- MatriceDeBase.h
- MatriceDeBase.cpp
- Matrice4x4.h
- Matrice4x4.cpp
![]()
Hiérarchie de classes
| Vecteur4 | CoordonneesHomogenes3D | Position3D | ||||
| Dimension3D | ||||||
| Matrice4x4 | TransformationGeometrique3D | Translation3D | ||||
| MatriceDeBase | Rotation3D | |||||
| Scale3D | ||||||
| LookAt | ||||||
| Rvb | Couleur | |||||
| Energie | ||||||
| Lumiere | LumierePonctuelle | LumiereSpot | ||||
| LumiereDirectionnelle | ||||||
| Materiel | ||||||
| Objet | Sphere | |||||
![]()


