Sujets et Corrections
de TD et TP
TD 2: Création de scènes OpenGL
TD 3: GLUt pour
les animations,
les contrôles
clavier et souris
TD 4: Les primitives
graphiques
en OpenGL
TD 5: La définition
et la réutilisation
d'objets
en VRML
TD 6: Mathématiques
des lumières
en Infographie:
la formule
de Lambert
TD 7: Les lumières
et matériaux
en OpenGL
TD 8: Les transformations
géométriques
et le processus
de visualisation
du point de vue
mathématique
TD 9: Le placage
de texture
en VRML
et en OpenGL
TD 10: Algorithmique
de l'Infographie:
Bresenham et
Cohen-Sutherland
TP 1-2: Prise
en mains des
environnements
de programmation
VRML et OpenGL
Notions initiales
sur les caméras
en OpenGL
TP 3-4: Primitives
graphiques
en OpenGL
Notions initiales
sur les lumières
en OpenGL
TP 5: Animation
sur les caméras
TP 6: Les lumières
et matériaux
en VRML
TP 7: Les lumières
et matériaux
en VRML
Dernière modification
16/11/09 07:03:34
TD 1: Création de scènes VRML
Exercice n°1
Programmer en VRML les scènes suivantes sans utiliser le nœud Separator:
Scène (1): Quatre cubes de coté de longueur 1.0 aux positions (2.0,0.0,2.0), (2.0,0.0,-2.0), (-2.0,0.0,2.0) et (-2.0,0.0,-2.0).
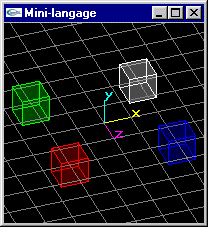
Scène (2): Même scène que la scène (1), mais le cube en position (2.0,0.0,2.0) subit une rotation de 45° autour de l'axe y passant par son centre.
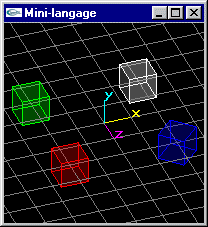
Scène (3): Même scène que la scène (2), mais le cube en position (2.0,0.0,-2.0) subit un zoom de rapport (1.0,1.0,2.0) par rapport à son centre.

Scène (4): Même scène que la scène (3), mais le cube en position (-2.0,0.0,-2.0) subit une rotation de 30° autour de l'axe y passant par son centre et un zoom de rapport (1.0,1.0,2.0) par rapport à son centre.
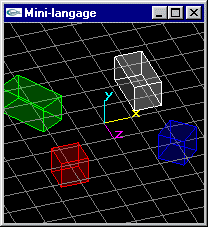
On s'autorise maintenant le nœud Separator
Programmer les scènes suivantes:
Scène (5): Même scène que la scène (4), mais on utilise le Separator pour éviter des transformations géométriques ayant pour but d'en annuler une autre.
Scène (6): Même scène que la scène (4), mais on utilise le Separator pour rendre les positions des objets indépendantes les une des autres.
Exercice n°2
Programmer la scène suivante:
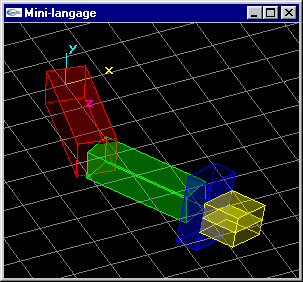
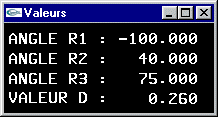
Un bras robot compose d'un avant-bras, d'un bras, et d'une paire de pinces. L'avant bras est articulé pour tourner autour de l'axe y d'un angle r1. Il s'agit d'un parallélépipède rectangle de dimension (3.0,1.0,1.0) (rouge). Le bras est articulé autour de l'axe y au bout de l'avant bras pour un angle r2. Il s'agit d'un parallélépipède rectangle de dimension (3.0,0.8,0.8) (vert). La pince est située au bout du bras. Elle peut tourner autour de l'axe du bras pour un angle r3. L'embase de la paire de pinces est un parallélépipède rectangle de dimension (0.6,1.2,1.8) (bleu). Chacune des mâchoires est un parallélépipède rectangle de dimension (1.0,1.2,0.4) (jaune) à même de se déplacer longitudinalement d'une valeur d pour réaliser une ouverture totale de 2xd.
TD 2: Implantation en OpenGL
Exercice 1
Réaliser l'implantation OpenGL des scènes de l'exercice 1 du TD 1.
Exercice 2
Réaliser l'implantation OpenGL de l'exercice 2 du TD 1.
Exercice 3
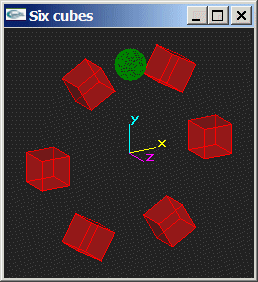
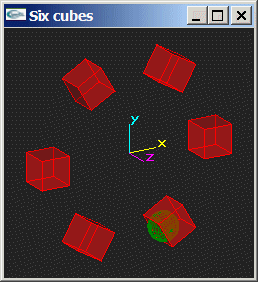
Soit la scène composée de six cubes de cotés 1 centrés sur les sommets d'un hexagone régulier de rayon 3 lui-même centré sur O et plongé dans le plan xOy. Les cubes doivent présenter une face directement orientée vers O.

Réaliser l'implantation OpenGL de cette scène.
TD 3: Utilisation de la librairie GLUt pour les animations, les contrôle clavier et souris
Exercice 1
Reprendre l'exercice n°3 du TD 2 pour programmer l'animation d'une sphère de rayon 0.5 sur une trajectoire circulaire de rayon 3 centrée sur O et plongée dans le plan xOy. Cette trajectoire amène la sphère à traverser les cubes. L'animation est réalisée à raison d'une image par degré de rotation. La sphère parcourt cycliquement cette trajectoire.
Exercice 2
Modifier l'animation précédente de manière qu'une fois revenue à son point de départ, la sphère reparte en sens inverse (et ainsi de suite).
Exercice 3
Modifier l'animation précédente de manière que l'utilisateur du programme puisse utiliser la touche Enter pour arrêter l'animation puis, par une nouvelle frappe de Enter, puisse relancer l'animation là où elle s'est arrêtée (et ainsi de suite).
Exercice 4
Modifier l'animation précédente de manière que l'utilisateur du programme puisse accélérer l'animation au moyen de la touche de curseur Up, et la ralentir au moyen de la touche de curseur Down.
Exercice 5
Modifier l'animation précédente de manière que l'utilisateur du programme puisse utiliser la souris pour inverser le sens de rotation par un clic.
GLUt |
||
| Les six cubes et la sphère animée | ||
TD 4: Les primitives graphiques en OpenGL
Exercice 1
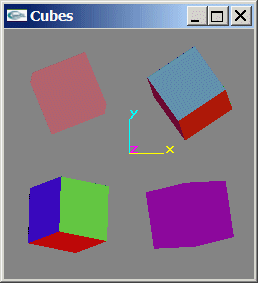
a) Ecrire une fonction de modélisation d'une boite cubique de dimension c centrée sur l'origine du repère. Cette fonction devra seulement assurer la création des facettes (cubes rouge et gris sur l'image proposée).
b) Modifier la fonction précédente pour y inclure la gestion des normales aux facettes (utilisées pour les calculs d'éclairages) (cubes bleu et vert sur l'image proposée).
Exercice 2
a) Ecrire une fonction de modélisation d'un cylindre de rayon r, de hauteur h, possédant n sections radiales, centré sur l'origine et d'axe y. Cette fonction devra seulement assurer la création des facettes (cylindres rouge et gris sur l'image proposée).
b) Modifier la fonction précédente pour y inclure la gestion des normales aux facettes (utilisées pour les calculs d'éclairages) (cylindres bleu et vert sur l'image proposée).

TD 5: La définition et la réutilisation d'objets en VRML
Voir dans le cours l'utilisation de:
Exercice 1
Soit la scène composée de quatre cubes de coté 1 centrés sur les sommets d'un carré de rayon 4 lui-même centré sur O et plongé dans le plan xOy, et de 4 cylindres de rayon 0.2 et de hauteur 4 joignant ces 4 sommets entre eux pour matérialiser les arêtes d'un carré de coté 4.


Ecrire un fichier VRML modélisant cette scène en utilisant les opérateurs DEF et USE.
Ecrire les fichiers VRML modélisant cette scène en utilisant le WWWInline.
Exercice 2
Soit la scène composée de huit cubes de coté 1 centrés sur les sommets d'un cube de rayon 4 lui-même centré sur O, et de 12 cylindres de rayon 0.2 et de hauteur 4 joignant ces 8 sommets entre eux pour matérialiser les arêtes du cube de coté 4.


Ecrire les fichiers VRML modélisant cette scène en utilisant le WWWInline.
- Modifier l'exercice précédent pour lier les cubes sommets vers l'URL http://www.univ-fcomte.fr.
Solutions
| Le DEF et le USE de l'exercice 1 |
| Le WWWInline de l'exercice 1 |
| Le WWWInline de l'exercice 2 |
| Le WWWAnchor de l'exercice 2 |
TD 6: Mathématiques des lumières en Infographie : la formule de Lambert
a) Définir une structure de données permettant de représenter une position dans un espace à trois dimensions.
b) Définir une structure de données permettant de représenter une direction dans un espace à trois dimensions.
c) Définir une structure de données permettant de représenter une couleur.
d) Définir une structure de données permettant de représenter une énergie lumineuse colorée.
e) Définir une structure de données permettant de représenter une source lumineuse ponctuelle.
f) Définir une structure de données permettant de représenter une source lumineuse directionnelle.
g) Définir une structure de données permettant de représenter un matériau du seul point de vue de la lumière diffuse.
On se donne une position p de l'espace. Cette position est extraite d'une surface s. La normale à s en p est la direction n. La surface est affectée du matériau m.
h) Ecrire une fonction de calcul de l'énergie lumineuse diffusée en p par la surface s soumise à l'éclairage d'une source lumineuse directionnelle ld.
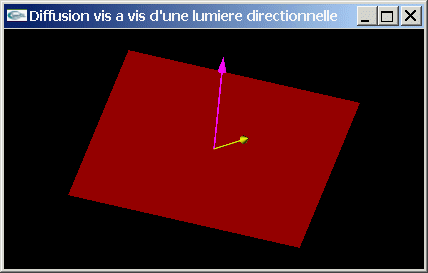
i) Ecrire une fonction de calcul de l'énergie lumineuse diffusée en p par la surface s soumise à l'éclairage d'une source lumineuse ponctuelle lp.
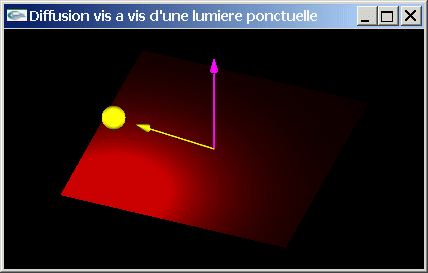
Solutions
GLUt |
||
| Structures de données | ||
| Energie diffusée sur lumière directionnelle | ||
| Energie diffusée sur lumière ponctuelle | ||
TD 7: Les matériaux et lumières en OpenGL
Exercice 1
Soit une scène composée d'un unique objet quelconque.
L'objet est affecté d'un matériau diffusant dans le blanc et réfléchissant
spéculairement dans le blanc.
Cet objet est éclairé au moyen de deux lumières. La première est ponctuelle et située
en position (1.0F,1.0F,3.0F). La seconde est directionnelle et provient de la direction
(-1.0F,-1.0F,3.0F). Les deux sont de couleur gris moyen tant en diffus qu'en spéculaire.
a) Dessiner cette scène.

b) Modifier cette scène pour que l'une des lumières devienne verte en spéculaire et l'autre bleue en spéculaire.


c) L'objet n'est pas animé, mais les deux lumières le sont. Elles réalisent un mouvement de rotation autour de l'axe Ox. Programmer cette animation.
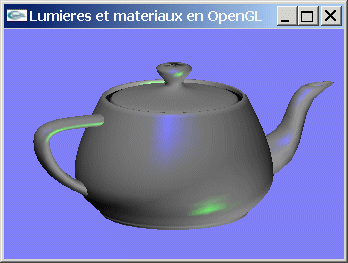
Exercice 2
Soit une scène composée de deux sphères rouge et verte en rotation l'une autour de l'autre. Programmer les matériaux de ces deux sphères de manière qu'ils soient transparents.
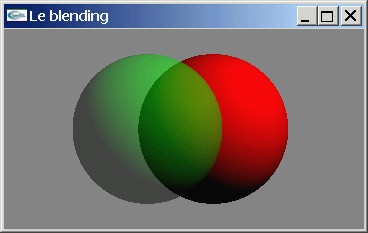



Exercice 3
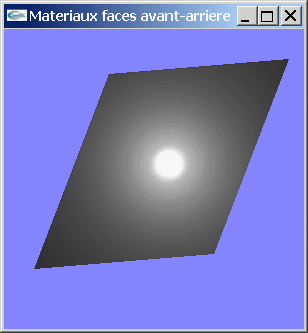
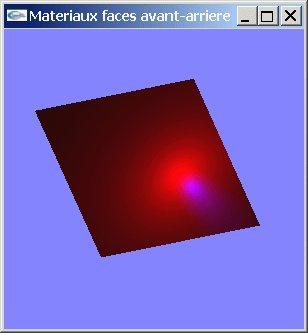
Soit une scène composée d'une facette éclairée par une source lumineuse. Dessiner cette facette de telle manière que sa face avant est affectée d'un matériel diffusant dans le blanc et réfléchissant spéculairement dans le blanc tandis que la facette arrière est définie avec un matériel diffusant dans le rouge et réfléchissant spéculairement dans le bleu.
Exercice 4
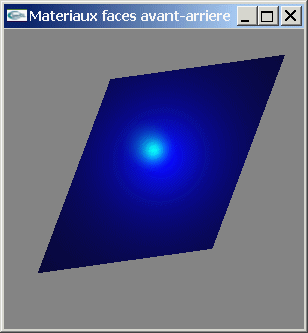
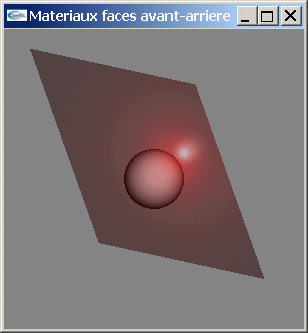
Soit une scène composée d'une facette éclairée par une source lumineuse située devant une sphère. La facette est dessinée de telle manière que sa face avant est affectée d'un matériel diffusant dans le bleu, réfléchissant spéculairement dans le vert et opaque tandis que la facette arrière est définie avec un matériel diffusant dans le rouge, réfléchissant spéculairement dans le blanc et opaque à 50%. La sphère est blanche en diffusion et n'est pas réfléchissante spéculairement.
Solutions
GLUt |
||
| Lumières et matériaux | ||
| La transparence | ||
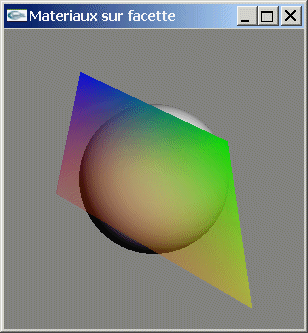
| Matériaux sur faces avant et arrière | ||
| Transparence sur faces avant et arrière | ||
TD 8: Les transformations géométriques et le processus de visualisation du point de vue mathématique
Exercice 1
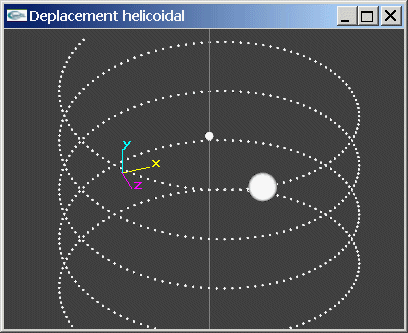
On souhaite réaliser l'implantation d'un mouvement hélicoïdal autour de l'axe de
direction ![]() passant par le point de coordonnées
passant par le point de coordonnées ![]() . Le mouvement est réalisé à raison d'un déplacement en y
de -2.0 par tour.
. Le mouvement est réalisé à raison d'un déplacement en y
de -2.0 par tour.
Définir la matrice de transformation assurant le calcul de la position Pi+1 à
une étape de l'animation à partir de la position Pi à l'étape précédente
pour une rotation de q radians entre deux étapes.

Exercice 2
On souhaite programmer un changement de repère de type repère global vers repère
observateur. Ces deux repères sont orthonormés.
On se donne la position Po de l'observateur dans le repère global qui devient l'origine
dans le repère observateur.
On se donne la position Pv d'un point visé par l'observateur. Ce point se trouvera sur
l'axe -Oz du repère observateur.
On considère que l'axe y du repère global (l'axe vertical) devra rester vertical vu
depuis l'origine dans la repère global.
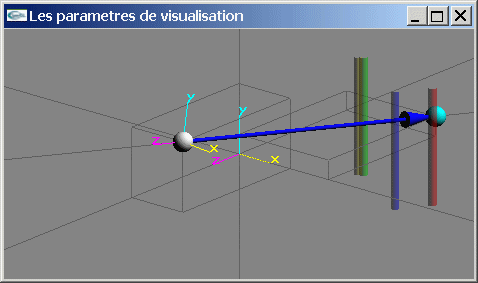
Point de vue sur une scène constituée de cylindres verticaux
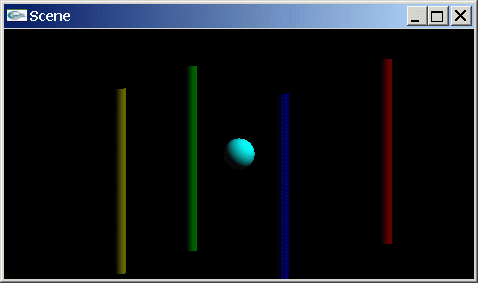
Image obtenue
a) Compte tenu de ces trois contraintes, définir une suite de transformations géométriques canoniques réalisant ce changement de repère.
b) Réaliser explicitement le produit de ces matrices pour obtenir une matrice de transformation M.
c) Réaliser le produit de M par le vecteur ![]() pour prouver l'hypothèse de conservation
des verticales.
pour prouver l'hypothèse de conservation
des verticales.
d) On se donne le vecteur ![]() =
= ![]() normé orienté de Po vers Pv. Se servir de ce vecteur pour simplifier la matrice M.
normé orienté de Po vers Pv. Se servir de ce vecteur pour simplifier la matrice M.
Solutions
GLUt |
||
| Un déplacement hélicoïdal | ||
| Définition d'une transformation de visualisation | ||
| Une transformation de visualisation | ||
TD 9: Le placage de texture en VRML et en OpenGL
Le placage de texture
Application en VRML
Application en OpenGL
Exercice 1 : VRML
Programmer une scène VRML quelconque avec les quatre objets (sphère, cube, cylindre, cône) de VRML. En affecter deux avec une texture dont la bitmap est codée dans le nœud et deux avec une texture dont la bitmap est extraite d'un fichier Jpeg. Mettre en évidence les problèmes liés au texturage 2D lors du placage sur un objet 3D.

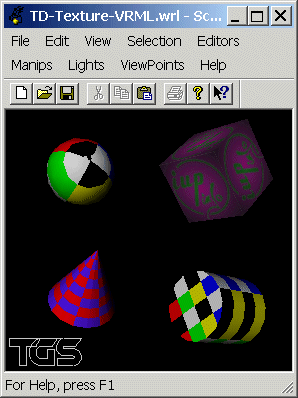
Solutions
Exercice 2 : OpenGL
Vérifier si le placage de texture fonctionne sur les objets GLUt.
Exercice 3 : OpenGL
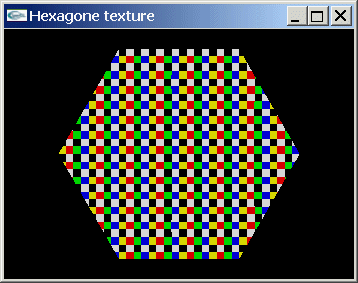
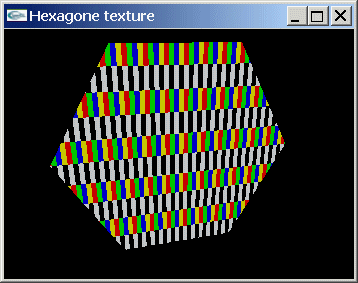
Programmer la création d'une texture bitmap définie sur un damier de 16 sur 16 pixels où des pixels blancs et noirs alternent sur les lignes paires et où des pixels jaunes, rouges, verts et bleus alternent sur les lignes impaires.
Programmer le placage de cette texture sur une facette hexagonale régulière. On intégrera la possibilité d'agrandir ou réduire la texture sur la facette.

Exercice 4 : OpenGL
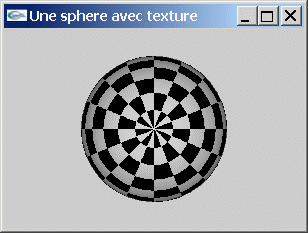
Programmer l'affichage d'une sphère revêtue d'une texture matérialisant un damier de 16x16 carrés noir et blanc.

Solutions
GLUt |
||
| Placage de texture sur objets GLUt | ||
| Placage de texture sur une facette hexagonale | ||
| Placage de texture sur une sphère | ||
TD 10: Algorithmique de l'Infographie: Bresenham et Cohen-Sutherland
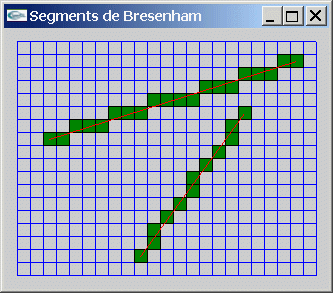
Soit l'algorithme de Bresenham pour le tracé de segments de pixels du premier octant.
void ligne(int xi,int yi,
int xf,int yf) {
int dx,dy,cumul,x,y ;
x = xi ;
y = yi ;
dx = xf - xi ;
dy = yf - yi ;
pixel(x,y) ;
cumul = dx / 2 ;
for ( x = xi+1 ; x <= xf ; x++ ) {
cumul += dy ;
if (cumul >= dx) {
cumul -= dx ;
y += 1 ; }
pixel(x,y) ; }
}
Exercice 1 : Bresenham
Implanter l'algorithme de Bresenham pour le dessin de segments 2D sur un écran bitmap (se restreindre au cas des segments du 1er octant). Le tracé devra être réalisé selon un motif répétitif sur 4 pixels avec 3 allumés puis 1 inchangé.
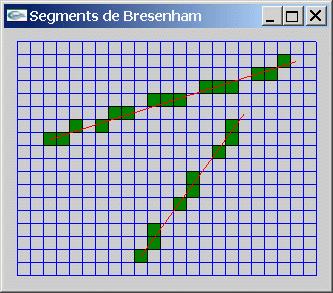
Exercice 2 : Bresenham
L'algorithme de Bresenham est un algorithme de dessin en 8-connexité.
Implanter une variante de cet algorithme pour le dessin en 4-connexité de segments 2D sur
un écran bitmap (se restreindre au cas des segments du 1er octant).
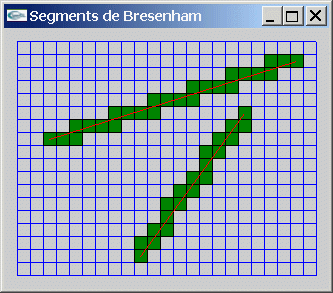
Exercice 3 : Bresenham
Implanter l'algorithme de Bresenham pour le dessin de segments 3D projetés sur un écran bitmap (se restreindre au cas des segments du 1er octant).
Exercice 4 : Cohen-Sutherland
1) Implanter une fonction de codage de la position d'un point vis à vis d'un rectangle de clipping dans le cadre de l'algorithme de Cohen-Sutherland.
2) Implanter une fonction de détermination de la position de l'intersection entre un segment arbitraire défini par ses extrémités et une droite horizontale.
3) Implanter une fonction de détermination de la position de l'intersection entre un segment arbitraire défini par ses extrémités et une droite verticale.
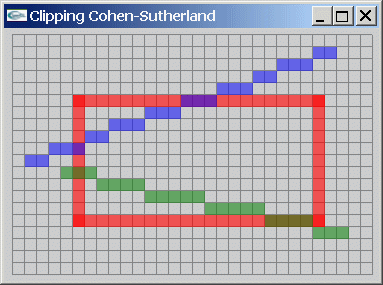
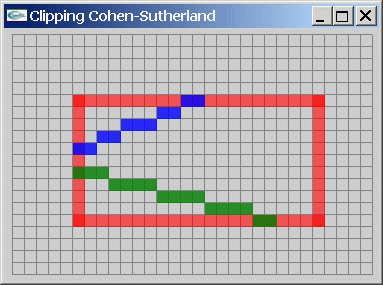
4) Se servir des fonctions précédentes pour implanter l'algorithme de Cohen-Sutherland.
5) Décrire une généralisation à la 3D de Cohen-Sutherland.
Solutions
GLUt |
||
| Algorithmes de Bresenham 2D | ||
| Algorithme de Bresenham 3D | ||
| Clipping de Cohen-Sutherland en 2D | ||
| Clipping de Cohen-Sutherland en 3D | ||
![]()
TP 1-2: Prise en mains des environnements de programmation VRML et OpenGL, notions initiales sur les caméras en OpenGL
Sous VRML:
- Un plugin Internet Explorer/Netscape Navigator (soit Cortona Player, soit Cosmo Player suivant les machines)
- Une application de visualisation (Scene Viewer)
Sous OpenGL:
- Visual C++ 6.0 sous Windows
- Cygwin g++ sous Windows
- g++ avec la librairie Mesa3D sous Linux
Travail demandé:
Sous VRML: Implantation des fichiers VRML du TD n°1.
Sous OpenGL:
Création d'un projet Visual C++ permettant la compilation OpenGL (bien spécifier les librairies OpenGL: OpenGL32.lib, glu32.lib et glut32.lib.
Téléchargement du source exemple destiné à être compilé: StarWarsIntro.cpp.
Dessin des objets de base GLUt pour repérer leurs caractéristiques de taille, d'orientation et de facettisation.
Implantation des exemples des TD n°2 et n°3 (en repartant de l'exemple précédent).
Exercice supplémentaire:
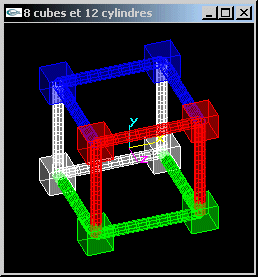
Soit la scène composée de huit cubes de cotés 1 centrés sur les sommets d'un cube de rayon 4 lui-même centré sur O, et de 12 cylindres de rayon 0.2 et de hauteur 4 joignant ces 8 sommets entre eux pour matérialiser les arêtes du cube de coté 4. Implanter cette scène.
GLUt |
||
| Les six cubes | ||
| Les six cubes et la sphère animée | ||
| Les huit cubes et douze cylindres | ||
| Star Wars Intro | ||
TP 3-4: Primitives graphiques en OpenGL, notions initiales sur les lumières en OpenGL
Exercice 1
a) Implanter les exercices du TD n°4 en version avec spécification des normales.
Il pourra être utile d'implanter une animation réalisant une rotation des objets cube et cylindre sur eux-mêmes car ceux-ci, dessinés sans éclairage et en perspective, peuvent être difficilement interprétables.


b) Sans éclairage, les normales ne sont pas utilisées.
-> Activation de la gestion de l'éclairage via l'exécution, dans la fonction init,
d'un glEnable(GL_LIGHTING).
L'éclairage est en fonctionnement, mais aucune lumière n'est allumée
donc les objets apparaissent en noir.
-> Activation de la première lumière via l'exécution, dans la fonction init, d'un
glEnable(GL_LIGHT0).
c) Cette lumière est par défaut une lumière directionnelle fournissant un éclairage vu selon l'axe (0.0,0.0,1.0). Modifier cette direction en utilisant le code suivant dans la fonction init:
float dir[] = { 1.0F,0.0F,0.0F,0.0F} ;
glLightfv(GL_LIGHT0,GL_POSITION,dir);
-> L'éclairage provient de la droite.
De la même manière, la première lumière possède le blanc pour couleur par défaut. Modifier cette couleur en utilisant le code suivant dans la fonction init:
float jaune[] = { 1.0F,1.0F,0.0F,1.0F} ;
glLightfv(GL_LIGHT0,GL_DIFFUSE,jaune);
d) Les sommets et normales spécifiés dans une primitive seront soumis
aux translations, rotations et mises à l'échelle réalisées sur la primitive. Avec les
translations et les rotations, il n'y a pas de problème. En revanche, avec les mises à
l'échelle, les normales se verront allongées ou réduites et ne seront donc plus
normées.
-> On exécute un glEnable(GL_NORMALIZE) dans la fonction init pour qu'OpenGL teste les
normales spécifiées et les normalisent si elles ne sont pas normées.
e) Ajouter d'autres lumières colorées à la scène (GL_LIGHT1, GL_LIGHT2, ...).
f) Affecter à chaque sommet de chaque facette une normale dirigée de l'origine vers le sommet.
g) Implanter le dessin de cylindres du TD n°4.
Exercice 2
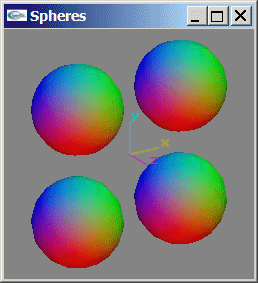
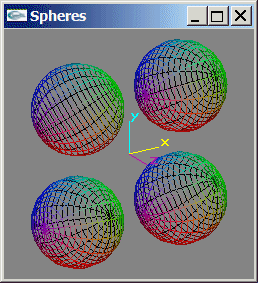
Implanter le dessin d'une sphère avec ses normales.
Exercice 3
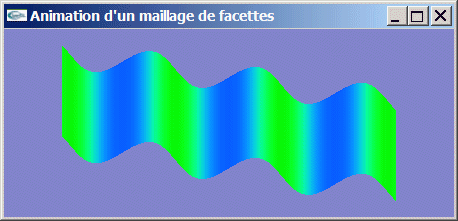
Implanter le dessin d'un tôle ondulée avec un mouvement de déplacement longitudinal de son ondulation.

Exercice 4
Implanter le dessin d'une onde circulaire progressant sur une surface liquide.
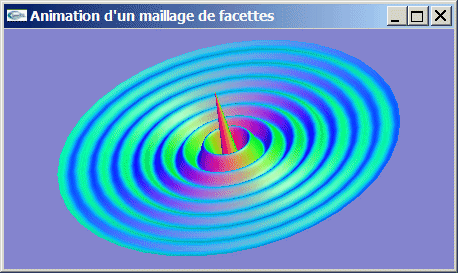

Pour les exercices 2, 3 et 4, on pourra avoir avantage à dessiner les
facettes en mode GL_LINE (i.e. par affichage de leurs bords) plutôt qu'en mode GL_FILL
(surfacique)
-> glPolygonMode(GL_FRONT_AND_BACK,GL_LINE);
Solutions
GLUt |
||
| Les boites parallèlipédiques par facettes | ||
| Les cylindres par facettes | ||
| Une tôle ondulante | ||
| Une onde circulaire progressante | ||
TP 5: Animation sur les caméras
Exercice 1
Implanter en OpenGL une animation de caméra consistant à effectuer un déplacement linéaire cyclique à travers une série de tores.

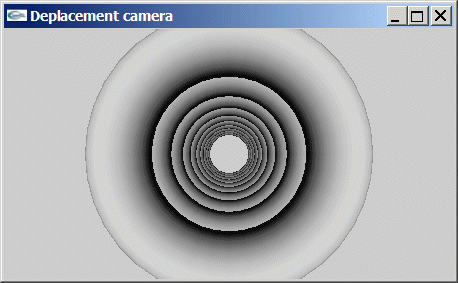
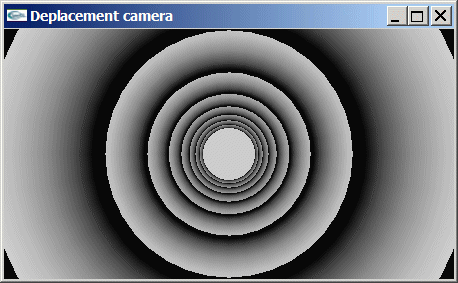
Exercice 2
Implanter en OpenGL une animation de caméra consistant à parcourir une trajectoire circulaire à l'intérieur d'un tore de carrés.
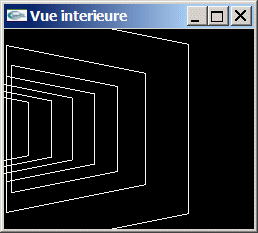
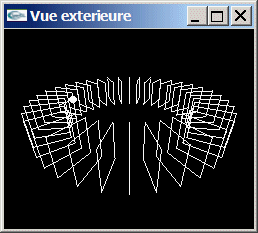
Exercice 3
Modifier l'exercice 2 pour autoriser le déplacement dans deux tores de carrés. Ces tores sont placés tangentiellement, l'utilisateur peut choisir avec le clavier de tourner dans l'un ou l'autre tore.

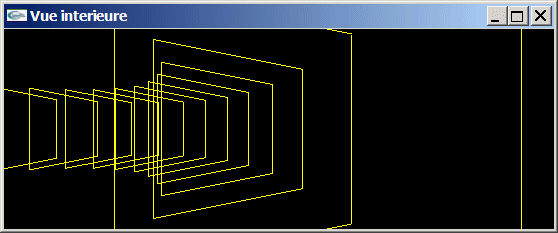
Vue instantanée 1
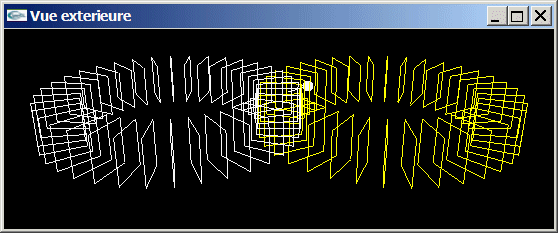

Vue instantanée 2
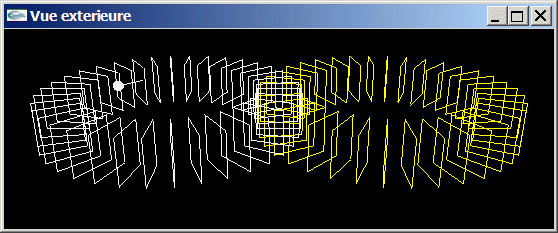

Vue instantanée 3
Solutions
GLUt |
||
| Traversée de tores alignés | ||
| Traversée d'un tore de carrés | ||
| Traversée de deux tores de carrés | ||
TP 6: Les lumières et matériaux en VRML
Exercice 1
a) Ecrire une scène composée d'une sphère de rayon 5 centrée sur
l'origine du repère et affectée d'un matériel avec uniquement de la diffusion dans le
rouge.
Tester avec et sans headlight.
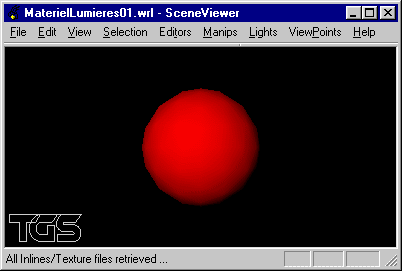
b) Modifier la scène précédente pour que le matériel intègre une réflexion spéculaire dans le vert.
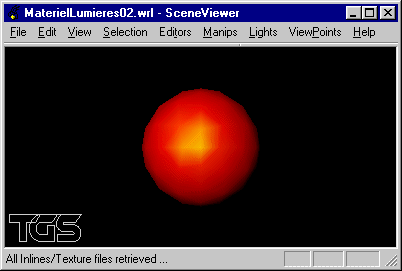
c) Modifier la scène précédente pour y intégrer un éclairage sous la forme d'une source lumineuse directionnelle blanche éclairant depuis la droite.
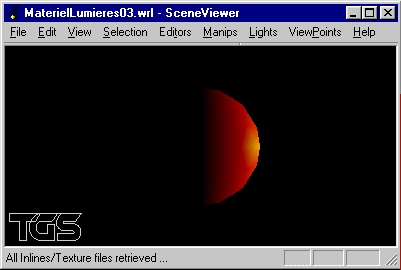
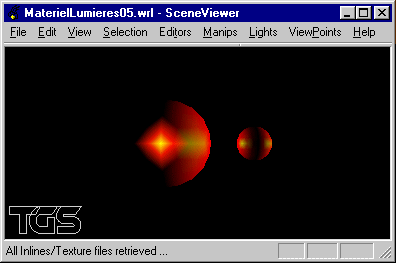
d) Modifier la scène précédente pour y inclure une seconde sphère de rayon 2 placée en position (10, 0, 0) possédant le même matériel que la première ainsi qu'une seconde source lumineuse ponctuelle blanche placée à l'origine.

e) Modifier la scène précédente pour y inclure une source lumineuse spot placée en position (0, 0, 10) orientée vers l'origine et éclairant partiellement la grosse sphère (éclipse à l'envers).
Solutions
VRML |
||||||
| Les fichiers VRML | ||||||
Exercice 2
Soient deux sphères de rayon 1, placées en position (5, 0, 0) et (-5, 0, 0) et blanches en diffusion. Soient deux sources lumineuses ponctuelles placées à l'origine du repère émettant dans le vert et dans le bleu. Construire la scène de telle manière que la sphère de droite soit éclairée uniquement par la lumière verte, et la sphère de gauche uniquement par la lumière bleue.
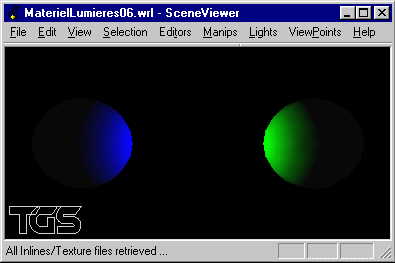
Modifier le matériau des deux sphères pour les rendre transparentes.
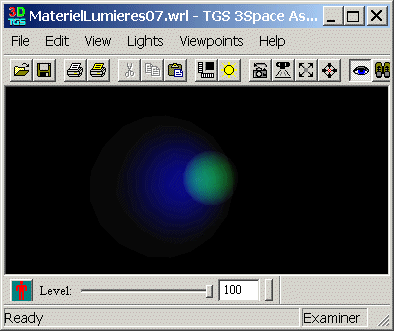
Solution
VRML |
||
| Le fichier VRML | ||
Exercice 3
Dans la mesure où le temps disponible le permet, tester la programmation des matériaux et lumières en OpenGL sur les exercices 1 et 2.
TP 7: Les lumières et matériaux en OpenGL
Exercice 1
Soit une scène composée d'une unique sphère de rayon 5 placée en position
(0.0,0.0,0.0).
Cette sphère diffuse dans le blanc et réfléchit spéculairement dans le jaune.
Elle est éclairée par deux sources lumineuses.
La première source est directionnelle de direction (-3.0,0.0,3.0) et possède la couleur
rouge en diffusion et la couleur verte en spéculaire.
La seconde est un spot de position (10.0,0.0,10.0), d'ouverture 15° et de direction
orientée vers le centre du repère. Il est de couleur bleue en diffusion et blanche en
spéculaire.
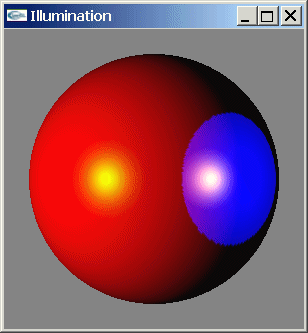
a) Programmer l'affichage statique de cette scène.
b) Programmer une animation où le spot (uniquement lui) fait le tour de la sphère (rotation autour de l'origine et dans le plan xOz).

Exercice 2
Prouver par un exemple que le résultat d'un affichage OpenGL avec blending dépend de
l'ordre dans lequel les objets sont tracés.
Sur les machines sous Windows NT 4.0 et munie de cartes graphiques ATI Xpert 2000 Pro, il
est nécessaire de configurer le blending via l'exécution de la ligne de code:
glBlendFunc(GL_SRC_ALPHA,
GL_ONE_MINUS_SRC_ALPHA);
Sur les autres machines, il semble que cette configuration soit réalisée
par défaut.
Exercice 3
Tester l'affectation de matériaux différents aux trois sommets d'une facette quadrangulaire.
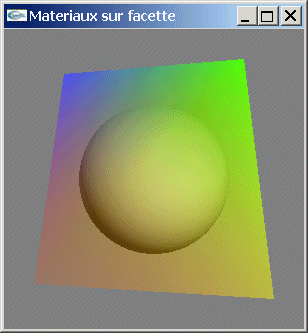
Solutions
![]()
TP 8: Algorithmique de l'Infographie: Cohen-Sutherland
1) Implanter les structures de données suivantes:
- position d'un point dans un espace à deux dimensions,
- segment de droite,
- rectangle,
- code de repérage pour l'algorithme de Cohen-Sutherland.
2) Implanter une fonction de détermination du code de repérage de Cohen-Sutherland pour une position dans un rectangle.
3) Implanter une fonction de test de l'égalité à 0 de l'intégralité d'un code
4) Implanter une fonction de calcul du "et binaire" entre deux codes.
5) Implanter un programme OpenGL
- permettant de dessiner un rectangle et un segment,
- permettant de déplacer les extrémités du segment,
- affichant les codes des deux extrémités,
- affichant le type de cas de Cohen-Sutherland pour le placement du segment vis à vis du rectangle.
6) Implanter une fonction permettant de déterminer la position de l'intersection entre la droite supportée par un segment et la droite verticale d'abscisse x.
7) Implanter une fonction permettant de déterminer la position de l'intersection entre la droite supportée par un segment et la droite horizontale d'ordonnée y.
8) Implanter une fonction à résultat booléen permettant de tester de la nième valeur d'un code.
8) Implanter l'algorithme de Cohen-Sutherland.