Sujets et Corrections
de TD et TP
TD n°1
Création de scènes
en VRML 1.0
TD n°2
Création de scènes
OpenGL
TD n°3
Utilisation
des primitives
graphiques
en OpenGL
TD n°4
Programmation
d'animations
en OpenGL
TD n°5
Caméras VRML
DEF et USE VRML
WWWInline VRML
TD n°6
Lumières et
matériaux en VRML
TD n°7
Mathématiques
de l'infographie
TD n°8
Mathématique de l'infographie
Test d'intersection
rayon-sphère
TD n°9
Calculs d'ombrage
par la formule
de calcul
de la réflexion
diffuse
de Lambert
TD n°10
Le remplissage
de cercles
et de triangles 2D
TD n°11
BSplines
pour le lissage
de lignes polygonales
TP n°1
Prise en mains
d'un environnement
de programmation
VRML
TP n°2
Prise en mains
d'un environnement
de programmation
OpenGL
TP n°5
Matériaux et
lumières en OpenGL
TP n°6
Mathématiques
pour l'infographie
TP n°7
Mathématiques
pour l'infographie
(suite)
TP n°8
Correction
de l'examen
de TD n°1
TP n°9
Calculs géométriques
pour les réflexion
et réfraction
TP n°10
Remplissage
d'une facette
triangulaire 2D
TP n°11
Le placage
de texture
en VRML
et en OpenGL
Dernière modification
16/11/09 07:03:35
TD n°1: Création de scènes VRML 1.0
Exercice n°1
(1) Programmer en VRML la scène suivante sans utiliser le nœud Separator ailleurs que pour le Separator d'encadrement global du fichier:
Quatre cubes de coté de longueur 1.0 aux positions (2.0,0.0,2.0), (2.0,0.0,-2.0), (-2.0,0.0,2.0) et (-2.0,0.0,-2.0).
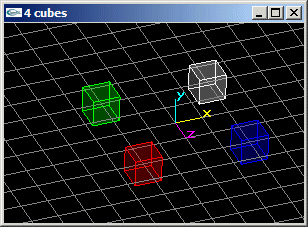
(2) Reprogrammer en VRML la scène précédante en utilisant le nœud Separator pour rendre les objets indépendants les uns des autres.
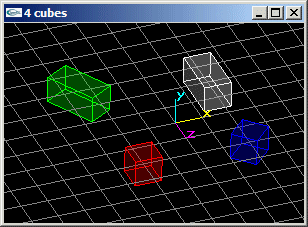
(3) Reprogrammer en VRML la scène précédante en apportant les modifications suivantes:
- Le cube en position (2.0,0.0,2.0) subit une rotation de 45° autour de l'axe y passant par son centre.
- Le cube en position (2.0,0.0,-2.0) subit un zoom de rapport (1.0,1.0,2.0) par rapport à son centre.
Le cube en position (-2.0,0.0,-2.0) n'est plus centré en ce point. Il est placé de telle manière qu'il présente une rotation de 30° autour de l'axe y passant par le sommet (-2.0,0.0,-2.0) et que ce sommet soit le centre de sa base inférieure. En outre, il subit un zoom de rapport (1.0,1.0,2.0) par rapport à son centre.
Exercice n°2
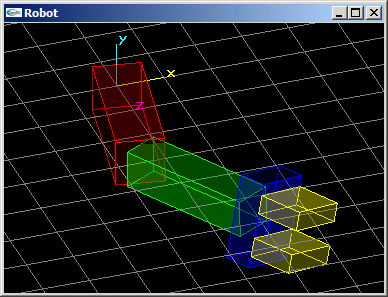
Programmer la scène modélisant un bras robot composé d'un avant-bras,
d'un bras, et d'une paire de pinces.
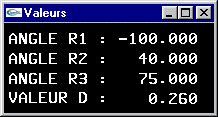
L'avant-bras est articulé pour tourner autour de l'axe y d'un angle r1. Il s'agit d'un
parallélépipède rectangle de dimension (3.0,1.0,1.0) (rouge). Le bras est articulé
autour de l'axe y au bout de l'avant bras pour un angle r2. Il s'agit d'un
parallélépipède rectangle de dimension (3.0,0.8,0.8) (vert). La pince est située au
bout du bras. Elle peut tourner autour de l'axe du bras pour un angle r3. L'embase de la
paire de pinces est un parallélépipède rectangle de dimension (0.6,1.2,1.8) (bleu).
Chacune des mâchoires est un parallélépipède rectangle de dimension (1.0,1.2,0.4)
(jaune) à même de se déplacer longitudinalement d'une valeur d pour réaliser une
ouverture totale de 2xd.
TD n°2: Création de scènes OpenGL
Exercice n°1
Soit la scène composée de n cubes de cotés 1 centrés sur les sommets d'un polygone régulier de rayon 3 lui-même centré sur O et plongé dans le plan xOy. Les cubes doivent présenter une face directement orientée vers O.

Réaliser l'implantation OpenGL de cette scène en une fonction C.
Exercice n°2
Soit la scène composée de huit cubes de cotés 1 centrés sur les
sommets d'un cube de rayon 4 lui-même centré sur O, et de 12 cylindres de rayon 0.25 et
de longueur 3.0 joignant ces 8 sommets entre eux pour matérialiser les arêtes du cube de
coté 4.
Implanter cette scène en une fonction C.

Fichiers sources pour dessiner des cylindres
ModuleCylindres.cpp
ModuleCylindres.h
TD n°3: Les primitives graphiques en OpenGL
Exercice n°1
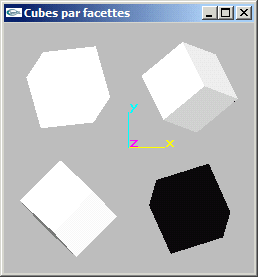
a) Ecrire une fonction de modélisation d'une boite cubique de dimension c centrée sur l'origine du repère. Cette fonction devra seulement assurer la création des facettes (cubes blanc et noir uniforme sur l'image proposée).
b) Modifier la fonction précédente pour y inclure la gestion des normales aux facettes (utilisées pour les calculs d'éclairages) (cubes gris ombrés sur l'image proposée).
Exercice n°2
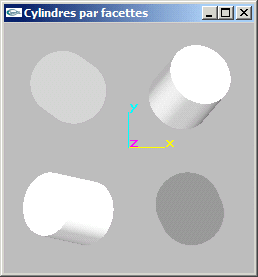
a) Ecrire une fonction de modélisation d'un cylindre de rayon r, de hauteur h, possédant n sections radiales, centré sur l'origine et d'axe y. Cette fonction devra seulement assurer la création des facettes (cylindres gris uniformes sur l'image proposée).
b) Modifier la fonction précédente pour y inclure la gestion des normales aux facettes (utilisées pour les calculs d'éclairages) (cylindres avec ombrage gris sur l'image proposée).
TD n°4: Programmation d'animations en OpenGL
Exercice n°1
On considère une scène quelconque modélisée par une fonction void
scene(void).
Ecrire les fonctions display et idle d'un programme C+OpenGL permettant d'afficher et
d'animer cette scène par rotation autour de l'axe Oz.
Exercice n°2
Modifier l'exercice précédent pour y inclure un contrôle clavier permettant d'activer/désactiver l'animation au moyen de la touche enter.
Exercice n°3
Effectuer une nouvelle modification de telle sorte que la touche espace permette de changer le sens de rotation.
Exercice n°4
Programmer l'affichage d'une mouette stylisée par:
- un corps sphéroïde,
- une aile droite en deux éléments sphéroïdes articulés,
- une aile gauche en deux éléments sphéroïdes articulés.
Animer cette mouette pour qu'elle batte des ailes.


GLUt |
||
| Scène animée par rotation autour de Oz | ||
| La mouette | ||
TD n°5: Les caméras en VRML,
le DEF et USE VRML, le WWWInline VRML
Exercice n°1
On considère une scène VRML quelconque centrée sur l'origine du repère
et contenue dans un volume approximativement sphèrique de rayon 5.
On souhaite visualiser en gros plan cette scène au moyen d'une caméra de visualisation
en projection en perspective.
Définir les paramètres d'une telle caméra pour les points de vue
suivants:
- (0.0, 0.0, 100.0),
- (0.0, 0.0, -100.0),
- (100.0, 0.0, 100.0),
- (100.0, 100.0, 100.0).
Exercice n°2
Modéliser un croisillon 3D de six flèches constituées individuellement
d'un cylindre de hauteur 2.0 et de rayon 0.25 et d'un cone de hauteur 3.0 et de rayon 0.5.
Utiliser le WWWInline de VRML pour le processus
de modélisation.

Exercice n°3
Modifier l'exercice précédent pour utiliser le DEF et le USE VRML pour simplifier l'écriture.
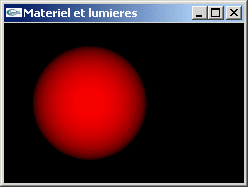
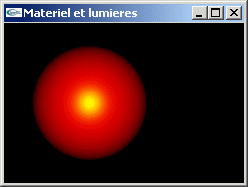
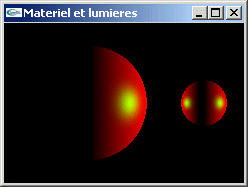
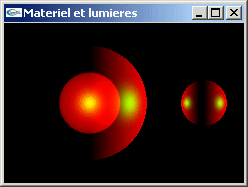
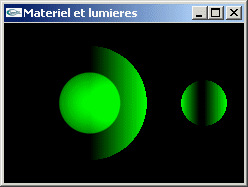
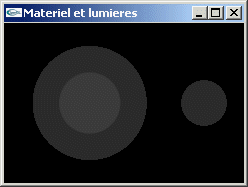
TD n°6: Matériaux et lumières en OpenGL
Gestion en OpenGL des matériaux et des lumières
Implanter en OpenGL les exercices du TP n°5.



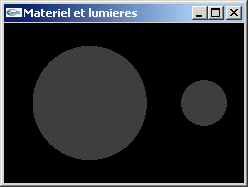
TD n°7: Mathématiques de l'infographie
Reprendre les exercices du TP n°6
Solution
TD n°8: Mathématiques de l'infographie: Test d'intersection rayon-sphère
Exercice n°1
Définir les classes C++ permettant de représenter les objets suivants:
- droite dans un espace 3D,
- surface sphérique.
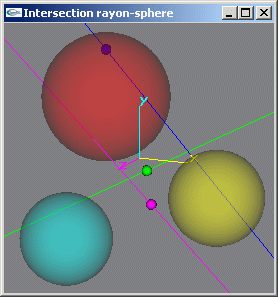
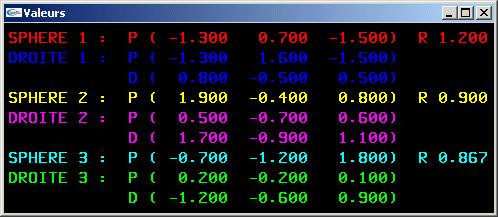
Exercice n°2
Implanter une méthode permettant de tester s'il existe une (ou plusieurs) intersection ou non entre une sphère et une droite.

Exercice n°3
Définir une classe C++ permettant de représenter un rayon lumineux du point de vue de ses seules caractéristiques géométriques.
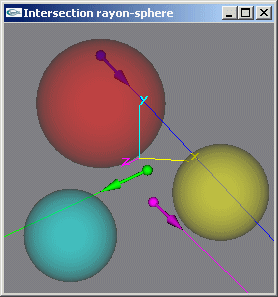
Exercice n°4
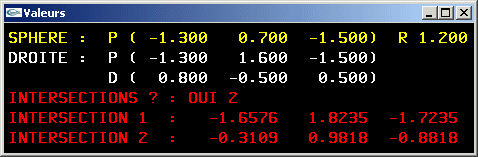
Implanter une méthode permettant de tester s'il existe une (ou plusieurs) intersection ou non entre une sphère et un rayon.
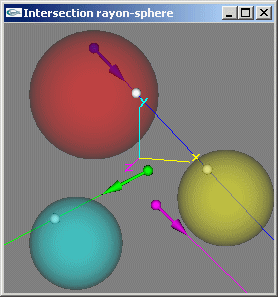
Exercice n°5
Implanter une méthode permettant de déterminer la position de l'intersection entre un rayon lumineux et une sphère la plus proche de la source du rayon lumineux.
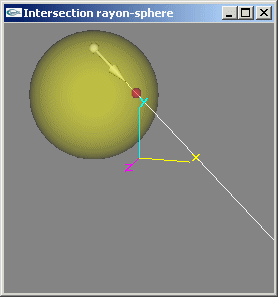
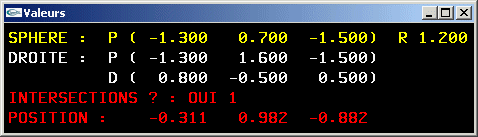
Solution
GLUt |
||
| Mathématiques pour l'infographie: Recherche de l'intersection entre un rayon et une sphère | ||
TD n°9: Calculs d'ombrage
Le but du TD est l'implantation des calculs mathématiques nécessaires à la
réalisation d'un calcul d'ombrage sur une surface diffusante éclairée par une source
lumineuse directionnelle.
On réutilisera les classes définies dans les TD/TP précédents.
Exercice n°1
Définir les classes C++ permettant de représenter les données suivantes:
- une couleur rvba,
- une énergie rvba,
- une source lumineuse directionnelle colorée,
- une source lumineuse ponctuelle colorée,
- un matériel permettant le paramétrage d'une réflexion diffuse.
Exercice n°2
Ecrire une méthode de calcul de l'énergie lumineuse colorée Ip reçue en une
position quelconque depuis une source lumineuse ponctuelle (énergie proportionnelle à la
quantité d'énergie émise et inversement proportionnelle au carré de la distance entre
la source lumineuse et le point considéré).
Les informations connues sont:
- la position du point où l'énergie reçue est évaluée,
- la source lumineuse ponctuelle colorée émettant de l'énergie.


Exercice n°3
Ecrire une méthode de calcul de l'énergie lumineuse colorée Ip reçue en une
position quelconque depuis une source lumineuse directionnelle (énergie proportionnelle
à la quantité d'énergie émise).
Les informations connues sont:
- la position du point où l'énergie reçue est évaluée,
- la source lumineuse directionnelle colorée émettant de l'énergie.

Exercice n°4
Ecrire une méthode de calcul de l'énergie lumineuse colorée diffusée (formule de Lambert, L = Ip Kd (![]() .
.![]() )) en un point d'une surface
éclairé par une source lumineuse ponctuelle.
)) en un point d'une surface
éclairé par une source lumineuse ponctuelle.
Les informations connues sont:
- la position du point où la diffusion est évaluée,
- le matériel dont la surface est munie,
- la source lumineuse directionnelle éclairant la surface,
- la normale à la surface au point de diffusion.

Exercice n°5
Ecrire une méthode de calcul de l'énergie lumineuse colorée diffusée (formule de Lambert, L = Ip Kd (![]() .
.![]() )) en un point d'une surface
éclairé par une source lumineuse directionnelle.
)) en un point d'une surface
éclairé par une source lumineuse directionnelle.
Les informations connues sont:
- la position du point où la diffusion est évaluée,
- le matériel dont la surface est munie,
- la source lumineuse directionnelle éclairant la surface,
- la normale à la surface au point de diffusion.
Exercice n°6
Utiliser les méthodes des questions (4) et (5) pour réaliser le calcul d'éclairage
par diffusion des trois sommets d'une facette triangulaire munie d'un matériel sous une
source lumineuse directionnelle ou ponctuelle colorée.
Utiliser le lissage des couleurs
qu'OpenGL peut générer sur une facette pour illustrer l'ombrage complet de la facette.
Adapter le programme précédent au dessin d'une sphère sous l'éclairage d'une source
lumineuse directionnelle ou ponctuelle colorée.
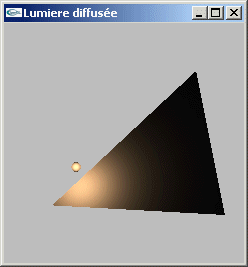
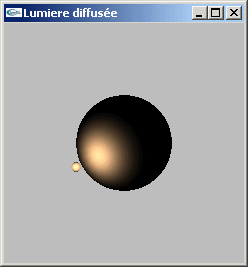
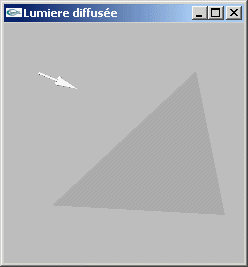

Solutions
GLUt |
||
| Energie diffusée par une surface sous lumière directionnelle ou ponctuelle |
||
TD n°10: Le remplissage de cercles et de triangles 2D
Exercice 1
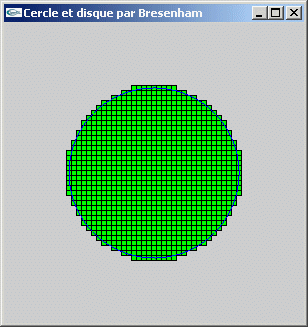
a) Implanter l'algorithme du midpoint (Bresenham) pour le dessin de cercles sur écran raster. On implantera une version simplifiée dessinant des cercles centrés sur l'origine.

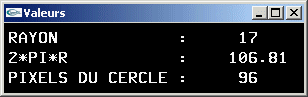
b) Ecrire une fonction permettant de tracer le segment horizontal de pixels allant du pixel (-x,y) au pixel (x,y).
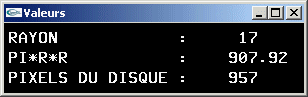
c) A partir des fonctions des questions a et b, implanter un algorithme de remplissage de cercles.
Exercice 2
a) On cherche à déterminer les pixels des bords d'une facette triangulaire définie
dans un espace 2D. Ecrire une fonction permettant de remplir un tableau indicé sur y,
pour tous les y où un segment 2D rectiligne est présent, avec l'abscice d'un des pixels
présents en cet y.
Le prototype de cette fonction pourra être:
int *extractionCote(int xi, int yi, int xf, int yf);
b) Ecrire une fonction permettant de tracer le segment horizontal de pixels allant du pixel (xi,y) au pixel (xf,y).
c) En utilisant les fonctions des questions a et b, écrire une fonction de remplissage
d'une facette triangulaire définie dans un espace 2D.
Le prototype de cette fonction pourra être:
void remplissageFacette(int x1, int y1, int x2, int y2, int x3, int y3);
On pourra supposer les sommets (x1,y1), (x2,y2) et (x3,y3) triés par ordre croissant
d'ordonnée.
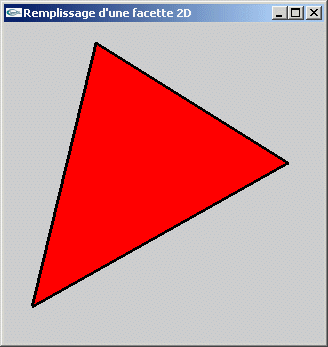
Solutions
TD n°11: Le lissage de lignes polygonales au moyen des BSplines
Exercice 1
Dans le but de l'implantation du dessin de courbes B-Splines en 3 dimensions, définir les classes suivantes:
- Position
- LignePolygonale
- MatriceDeBase
Exercice 2
Ecrire une fonction permettant de lisser une ligne polygonale à 4 sommets en une B-Spline selon une matrice de base particuliere.
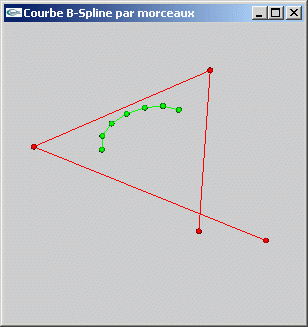
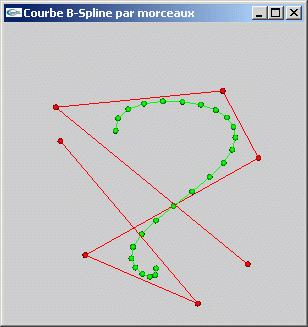
Courbe B-Spline NRU
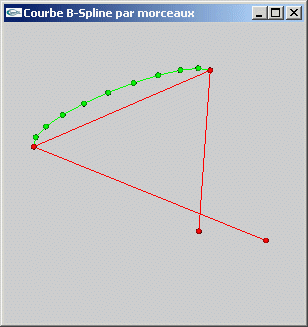
Courbe B-Spline de Catmull-Rom
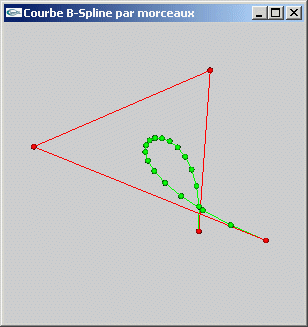
Courbe de Bézier
Exercice 3
Ecrire une fonction permettant de lisser une ligne polygonale au moyen d'un ensemble de B-Splines selon une matrice de base particulière.
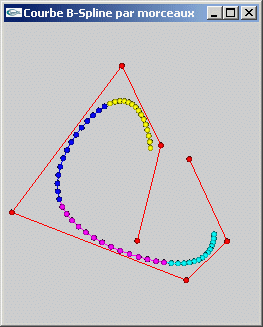 |
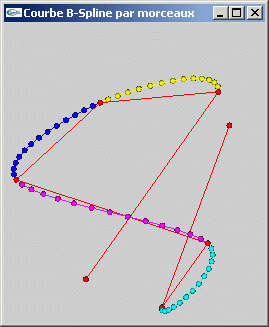 |
| Courbe B-Spline NRU | Courbe B-Spline de Catmull-Rom |
Solution
GLUt |
||
| Ligne polygonale lissée | ||
![]()
TP n°1: Prise en mains d'un environnement de programmation VRML
Les viewers disponibles sont:
- Un plugin Internet Explorer/Netscape Navigator (soit Cortona Player, soit Cosmo Player suivant les machines)
- Une application de visualisation (Scene Viewer)
Travail demandé:
- Implantation des fichiers VRML du TD n°1.
- Implantation d'une scène avec un cube, une sphère, un cylindre et un cone pour vérifier le centrage et l'axe de dessin de ces objets.
- Modification du bras robot pour que l'avant bras et le bras soient transformés en cylindres de diamètre 1.0 et 0.8 et de hauteur 3.0 et que l'articulation soit modélisée par un objet supplémentaire de type sphère de diamètre 1.4.

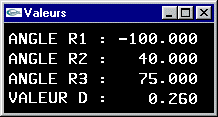
- Nouvelle modification du bras robot pour que les mandibules soient transformées en des cônes de rayon 0.2 et de hauteur 2.0 pointant vers l'intérieur de la pince avec un angle de r4 radians par rotation autour du centre de leurs bases.
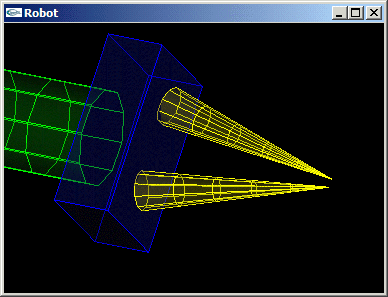
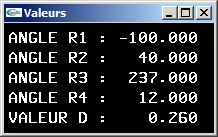
| Scène (2) |
| Scène (3) |
| Le bras robot |
| Test des objets |
| Le bras robot avec cylindres |
| Le bras robot avec cylindres et cones |
TP n°2: Prise en mains d'un environnement de programmation OpenGL
Création d'un projet Visual C++ permettant la compilation OpenGL
- Les fichiers d'inclusion (nécessaires à la compilation) spécifiques à OpenGL sont GL/gl.h et GL/glu.h ainsi que GL/glut.h si GLUT est utilisé.
- Les librairies d'édition de liens (nécessaires à la création de l'exécutable) spécifiques à OpenGL sont OpenGL32.lib et glu32.lib ainsi que glut32.lib si GLUT est utilisé.
- Les dll (nécessaires à l'exécution) spécifiques à OpenGL sont OpenGL32.dll et glu32.dll ainsi que glut32.dll si GLUT est utilisé.Téléchargement du programme source exemple minimum (ouverture d'une fenêtre et affichage d'un carré blanc) destiné à être testé: BeaucoupTropSimple.cpp. ATTENTION, ce programme n'est pas totalement fonctionnel car il ne gère pas correctement le fenêtrage ainsi que les événements associés.
Téléchargement du programme source exemple destiné à être testé: TropSimple.cpp. ATTENTION, ce programme n'est pas totalement fonctionnel car il ne gère toujours pas correctement le fenêtrage ainsi que les événements associés.
Téléchargement du programme source exemple destiné à être testé: Simple.cpp. Ce programme gère correctement le fenêtrage.
Téléchargement du programme source exemple fonctionnel (définition d'une caméra, gestion du clavier, gestion correcte du fenêtrage, dessin d'une scène élairée ou non) destiné à être testé: OpenGL.cpp.
Téléchargement du programme source exemple (animation) destiné à être testé: RollIt.cpp.
Dessin des objets de base GLUt pour repérer leurs caractéristiques de taille, d'orientation et de facettisation (en repartant de l'exemple OpenGL.cpp).
Implantation des exercices du TD n°2 (en repartant de l'exemple OpenGL.cpp).
Fichiers sources pour dessiner des cylindres
ModuleCylindres.cpp
ModuleCylindres.h
TP n°3: GLUT
Exercice n°1
Programmez une application OpenGL affichant une petite sphère dans une fenêtre et permettant à l'utilisateur de cliquer au moyen de la souris pour déplacer cette sphère instantanément là où le clic a eu lieu.
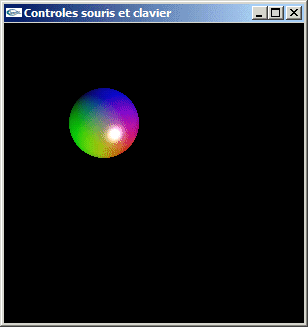
Exercice n°2
Programmez une application OpenGL affichant une petite sphère dans une fenêtre et permettant à l'utilisateur de glisser déplacer (drag and drop) cette sphère au moyen de la souris.
Exercice n°3
Reprendre l'exercice 2 précédent pour y inclure des contrôles clavier permettant de déplacer la sphère via les touches de curseur et d'augmenter et diminuer son diamètre via les touches + et -.
On pourra s'inspirer du programme source suivant qui
définit un volume de visualisation tel que les coordonnées obtenues au moyen des
fonctions de gestion de la souris de GLUT lors de clics sont directement des coordonnées
utilisables dans le repère de modélisation.
-> les x et y souris sont les mêmes que les x et y du repère d'origine de la scène.
ReperesSceneEtSourisIdentiques.cpp
TP n°4: Les caméras OpenGL
Exercice n°1
On considère le code source OpenGL suivant:

Il n'intègre pas la gestion du redimentionnement de la fenêtre d'affichage qu'autorise GLUT via une fonction reshape mais va nous permettre de tester différents types de caméra.
a) Quelle est la caméra implantée dans ce code source?
b) Modifier cette caméra pour la changer en une caméra de visualisation en projection en perspective de position "identique" visualisant la scène en gros plan.
c) Reculer la position de la caméra d'un facteur 10 de manière à prendre du "champ" pour moins déformer l'affichage de la scène à l'écran.
Exercice n°2
Modifier l'exercice précédent pour intégrer la gestion des
redimensionnements fenêtre via la fonction reshape de GLUT. On préservera un ratio
largeur/hauteur de la caméra égal au ratio largeur/hauteur de la fenêtre.
Pour bien suivre le fonctionnement du programme, on pourra ajouter un
printf("Display\n"); dans la fonction display et un
printf("Reshape\n"); dans la fonction reshape.
Exercice n°3
Modifier de nouveau l'exercice précédent pour placer la caméra selon de point de vue de position (100.0, 50.0, 100.0) regardant en direction de l'origine (0.0, 0.0, 0.0) avec pour verticale (0.0, 1.0, 0.0).

Exercice n°4
Apporter une dernière modification pour animer la caméra de visualisation pour la faire tourner autour de la scène par rotation autour de l'axe Oy en passant par la position (100.0,50.0,100.0) tout en la faisant regarder en direction de l'origine.
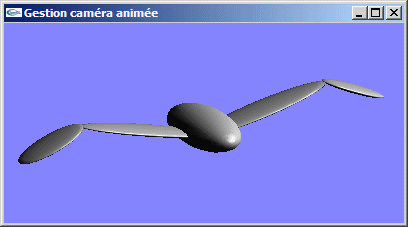
GLUt |
||
| Gestion minimum d'une caméra (1a) | ||
| Gestion minimum d'une caméra (1b) | ||
| Gestion minimum d'une caméra (1c) | ||
| Gestion complète d'une caméra | ||
| Point de vue | ||
| Animation de caméra (version 1) | ||
| Animation de caméra (version 2) | ||
TP n°5: Matériaux et lumières en VRML
Gestion en VRML des matériaux et des lumières
Exercice 1
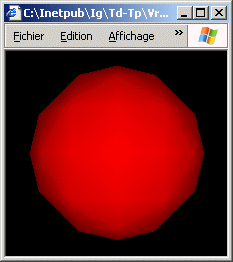
a) Ecrire une scène VRML composée d'une sphère de rayon 5 centrée sur l'origine du repère et affectée d'un matériel avec uniquement de la diffusion dans le rouge. Tester l'activation/désactivation de la lampe frontale.
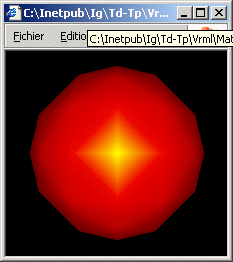
b) Modifier la scène précédente pour que le matériel intègre une réflexion spéculaire dans le vert.
c) Modifier la scène précédente pour y intégrer un éclairage sous la forme d'une source lumineuse directionnelle blanche éclairant depuis la droite. Désactiver la lampe frontale.

d) Modifier la scène précédente pour y inclure une seconde sphère de rayon 2 placée en position (10, 0, 0) possédant le même matériel que la première ainsi qu'une seconde source lumineuse ponctuelle blanche placée à l'origine.
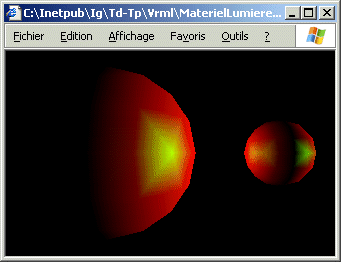
e) Modifier la scène précédente pour y inclure une source lumineuse
spot placée en position (0, 0, 10) orientée vers l'origine et éclairant partiellement
la grosse sphère.
Tester les différentes préférences de votre viewer VRML.

Solutions
VRML |
||||||
| Les fichiers VRML | ||||||
Exercice 2
Reprendre l'exercice précédent avec le matériel suivant:
Material {diffuseColor 0 1 0
specularColor 0 0 1
shininess 0.25
ambientColor 1 0 0
emissiveColor 0.2 0.2 0.2
transparency 0
}
Analyser les contributions respectives des différentes caractéristiques.
Solution
VRML |
||||||
| Les fichiers VRML | ||||||
TP n°6: Mathématiques pour l'infographie
Le TP est à réaliser en programmation orientée objet.
1) Définir une classe permettant de représenter une position dans un espace à 3 dimensions réelles.
2) Définir une classe permettant de représenter une direction dans un espace à 3 dimensions réelles.
3) Ecrire une méthode de calcul de la direction définie entre deux positions.
4) Ecrire une méthode de calcul de la norme d'une direction.
5) Ecrire une méthode de normalisation d'une direction.
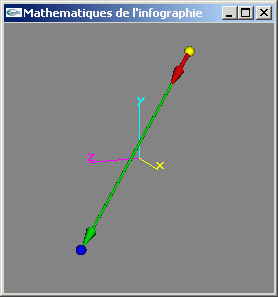

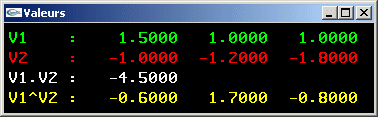
6) Ecrire une méthode de calcul du produit scalaire de deux directions.
7) Ecrire une méthode de calcul du produit vectoriel de deux directions.


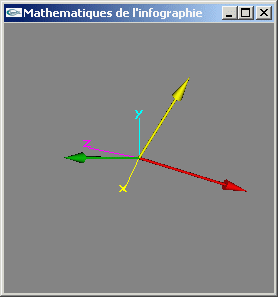
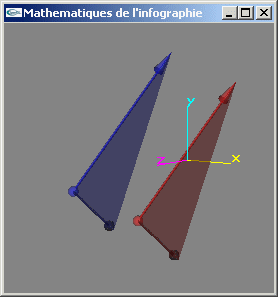
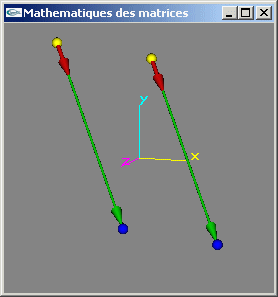
8) Définir une classe permettant de représenter une facette triangulaire d'un espace à 3 dimensions.
9) Ecrire une méthode de calcul d'une des deux normales à une facette triangulaire.
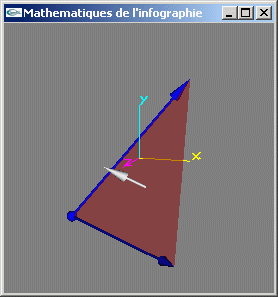
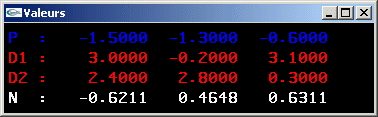
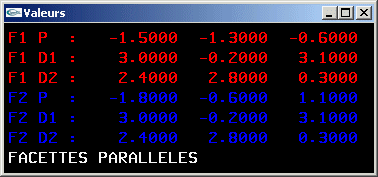
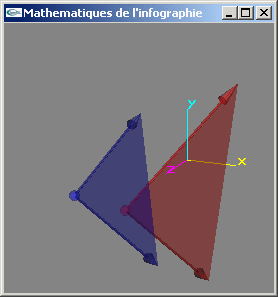
10) Ecrire une méthode de test du parallélisme entre deux facettes triangulaires.
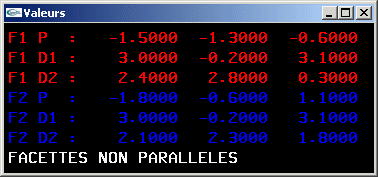
Solution
TP n°7: Mathématiques pour l'infographie (suite)
Ce TP s'inscrit dans la continuité du TP n°6.
1) Définir une classe mère transformation géométrique (variables membres, constructeurs, destructeur).
2) Définir une classe translation (variables membres, constructeurs, destructeur).
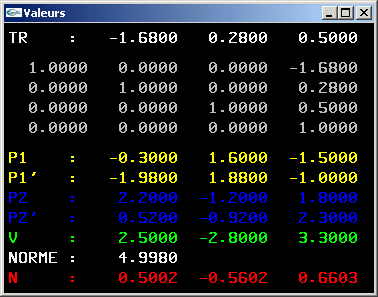
3) Définir une classe rotation (variables membres, constructeurs, destructeur).
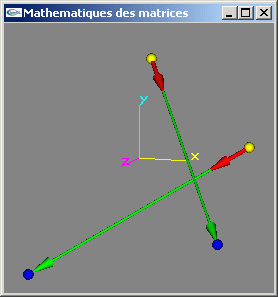
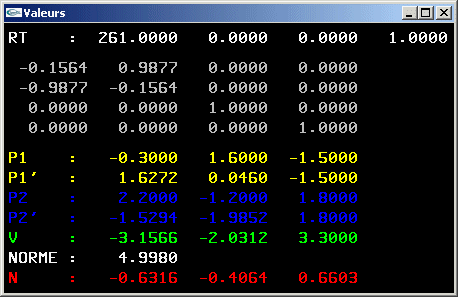
4) Définir une classe scale (variables membres, constructeurs, destructeur).
5) Implanter une méthode permettant d'appliquer une transformation géométrique à
une position ou une direction
(formule de calcul: wi =  , 1 <= i <= n, plus d'informations)
, 1 <= i <= n, plus d'informations)
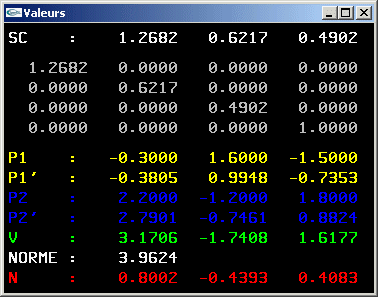
6) Implanter une méthode permettant de calculer la composition de deux transformations
géométriques
(formule de calcul: mij = 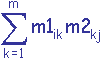 , 1 <= i <= n, 1 <= j <= p, plus d'informations).
, 1 <= i <= n, 1 <= j <= p, plus d'informations).
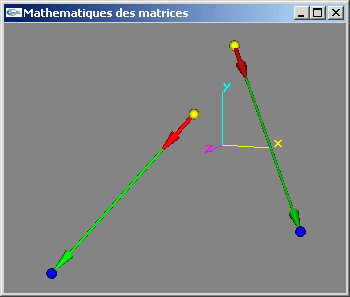
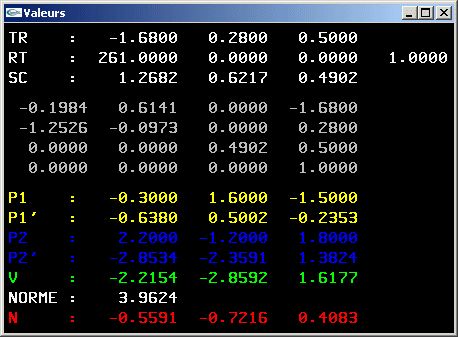
Solution
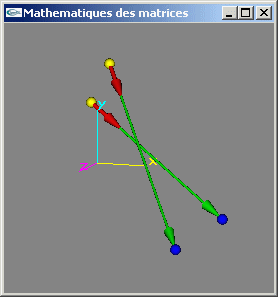
GLUt |
||
| Mathématiques pour l'infographie (suite) | ||
![]()
TP n°8: Correction de l'examen de TD n°1
On implantera les exercices 2, 3 et 4
Le fichier VRML aiguille est accessible à l'URL: Aiguille.wrl
![]()
TP n°9: Calculs géométriques pour les réflexion et réfraction
Exercice n°1
Le schéma suivant décrit le calcul géométrique du rayon de réflexion spéculaire généré à partir d'un rayon incident au niveau d'une interface entre deux milieux.

Le vecteur ![]() est le rayon incident. Le vecteur
est le rayon incident. Le vecteur ![]() est le vecteur normal à l'interface dans le milieu
"incident". qi est l'angle formé par
est le vecteur normal à l'interface dans le milieu
"incident". qi est l'angle formé par ![]() et
et ![]() . qr
est l'angle formé par
. qr
est l'angle formé par ![]() et le rayon réfléchi. La formule
suivante permet le calcul du rayon réfléchi
et le rayon réfléchi. La formule
suivante permet le calcul du rayon réfléchi ![]() .
.
![]()
Développer et tester une méthode de la classe Rayon (cf TD n°8) permettant de réaliser ce calcul.
Exercice n°2
Le schéma suivant décrit le calcul géométrique du rayon de transmission généré à partir d'un rayon incident au miveau d'une interface entre deux milieux.

Le vecteur ![]() est le rayon incident. Le vecteur
est le rayon incident. Le vecteur ![]() est le vecteur normal à l'interface dans le milieu
"incident". n est le rapport ni/nt entre les coefficients de diffusion ni et nt
des milieux d'incidence et de transmission. qi est l'angle
formé par
est le vecteur normal à l'interface dans le milieu
"incident". n est le rapport ni/nt entre les coefficients de diffusion ni et nt
des milieux d'incidence et de transmission. qi est l'angle
formé par ![]() et
et ![]() . qt est l'angle formé par -
. qt est l'angle formé par -![]() et le
rayon transmis. La formule suivante permet le calcul du rayon transmis
et le
rayon transmis. La formule suivante permet le calcul du rayon transmis ![]() .
.
![]()
Développer et tester une méthode de la classe Rayon (cf TD n°8) permettant de réaliser ce calcul.
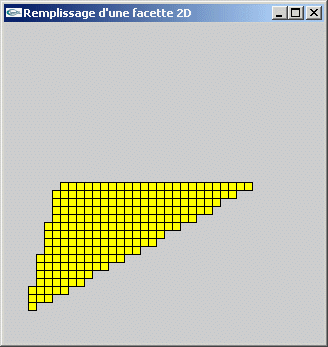
TP n°10: Remplissage d'une facette triangulaire 2D
On souhaite implanter une fonction de remplissage de facettes 2D par la méthode consistant à remplir de bas en haut par dessin successif des trames de pixels entre le bord gauche et le bord droit.
Question 1
On donne l'algorithme de Bresenham générique pour le dessin de segments:
void ligne(int xi,int yi,int xf,int yf) {
int dx,dy,i,xinc,yinc,cumul,x,y ;
x = xi ;
y = yi ;
dx = xf - xi ;
dy = yf - yi ;
xinc = ( dx > 0 ) ? 1 : -1 ;
yinc = ( dy > 0 ) ? 1 : -1 ;
dx = abs(dx) ;
dy = abs(dy) ;
allume_pixel(x,y) ;
if ( dx > dy ) {
cumul = dx / 2 ;
for ( i = 1 ; i <= dx ; i++ ) {
x += xinc ;
cumul += dy ;
if (cumul >= dx) {
cumul -= dx ;
y += yinc ; }
allume_pixel(x,y) ; } }
else {
cumul = dy / 2 ;
for ( i = 1 ; i <= dy ; i++ ) {
y += yinc ;
cumul += dx ;
if ( cumul >= dy ) {
cumul -= dy ;
x += xinc ; }
allume_pixel(x,y) ; } }
}
Utiliser et adapter cette fonction pour qu'elle réalise le calcul et le stockage dans un tableau de l'abscisse d'un pixel pour chaque ordonnée y du segment en paramètre.
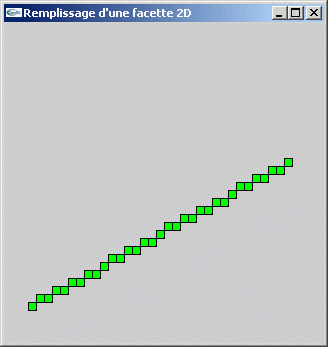

Question 2
Utiliser la fonction de la question 1 pour implanter une fonction de remplissage d'une facette triangulaire 2D.


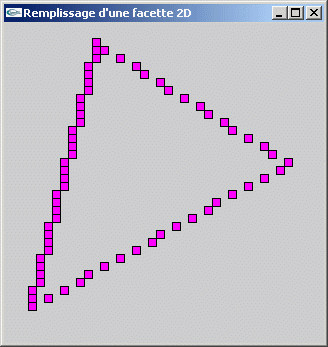
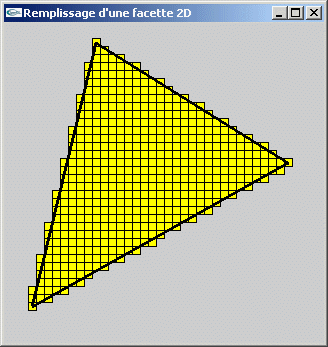
Question 3
Dans une version plus élaborée, on pourra s'intéresser au problème du choix du pixel le plus à droite ou du pixel le plus à gauche pour les bords droit et gauche qui présenteraient plus d'un pixel à droite ou à gauche sur certaines trames.
Solution
TP n°11: Placage de texture en OpenGL
Les principales fonctions OpenGL utilisées dans le cadre du texturage sont:
- glEnable(GL_TEXTURE_2D) pour activer le texturage 2 dimensions,
- glPixelStorei(GL_UNPACK_ALIGNMENT,1) pour permettre à OpenGL de travailler sur des bitmaps avec une précision de 1 pixel,
- glTexParameterf(GL_TEXTURE_2D,GL_TEXTURE_MAG_FILTER,GL_NEAREST)
et
glTexParameterf(GL_TEXTURE_2D,GL_TEXTURE_MIN_FILTER,GL_NEAREST)
pour spécifier la technique de placage de texture, - glTexImage2D(...) pour spécifier l'image à plaquer,
- glTexCoord2f(x,y) pour spécifier la prochaine coordonnée de texturage à utiliser.
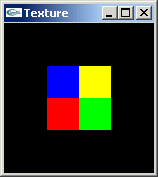
Exercice 1
a) Définir une fonction créant un tableau de pixels à même d'être utilisé dans un appel à glTexImage2D pour spécifier une texture de 2x2 pixels bleu et jaune pour la ligne du haut et rouge et vert pour la ligne du bas.

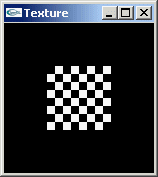
b) Reprendre la question précédente pour créer une bitmap d'un damier de 8 sur 8 pixels alternativement blanc et noir.

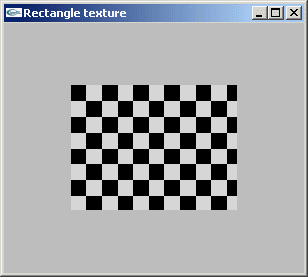
c) Tester ces fonction pour le placage de texture sur une facette rectangulaire de
taille 2.0 en x et 1.5 en y.
On proposera 2 alternatives de programmation:
(1) la texture reste carrée,
(2) la texture est déformée pour que ses sommets soient confondus avec ceux de la
facette.

Exercice 2
Dessiner un dé à jouer modélisé par un cube dont les facettes sont texturées.
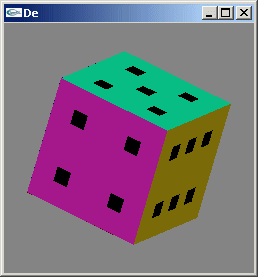
Exercice 3
Tester l'utilisation du canal alpha pour gérer des textures transparentes.
Sur le dé de l'exercice 2, les points seront opaques tandis que le reste de la facette
sera transparent.
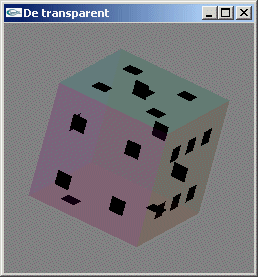
Solutions
![]()