Sujets et Corrections
de TD et TP
![]()
TD n°1
Création de scènes
en VRML 1.0
TP n°1
Prise en mains
d'un environnement
de programmation
VRML
TD n°2
Création de scènes
en OpenGL
TP n°2
Prise en mains
d'un environnement
de programmation
OpenGL
TD n°3
Utilisation
des contrôles
clavier et souris
avec GLUT
TP n°3
Utilisation
des contrôles
clavier et souris
avec GLUT
TD n°4
Utilisation
des primitives
graphiques OpenGL
TP n°4
La gestion
des caméras
en OpenGL
TD n°5
Animation
automatique
en OpenGL
TP n°5
Matériaux
et lumières
en VRML
TD n°6
Calcul
mathématique
de la diffusion
au moyen
de la formule
de Lambert
TP n°6
Matériaux
et lumières
en OpenGL
TD n°7
Mathématiques
pour l'infographie
TP n°7
Mathématiques
matricielles
TD n°8
Introduction
au plaçage
de texture
TP n°8
Plaçage de texture
en VRML
et OpenGL
TD n°9
Clipping par
l'algorithme
de Cohen-Sutherland
Dernière modification
16/11/09 07:03:36
TD n°1: Création de scènes VRML 1.0
Se référer à VRML 1.0, objets et nœuds pour la description des nœuds à utiliser.
(1) Programmer en VRML la scène suivante sans utiliser le nœud Separator ailleurs que pour le Separator d'encadrement global du fichier:
Quatre sphères de rayon 1.0 aux positions (2.0,0.0,2.0), (2.0,0.0,-2.0), (-2.0,0.0,2.0) et (-2.0,0.0,-2.0).
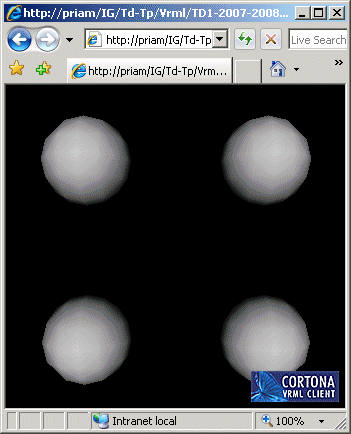
(2) Reprogrammer en VRML la scène de la question (1) en utilisant le nœud Separator pour rendre les objets indépendants les uns des autres.
(3) Reprogrammer en VRML la scène en apportant les modifications suivantes:
- La sphère en position (2.0,0.0,-2.0) subit une rotation de -45° autour de l'axe y passant par son centre.
- La sphère en position (2.0,0.0,2.0) subit un zoom de rapport (0.5,1.0,2.0) par rapport à son centre.
- La sphère en position (-2.0,0.0,2.0) n'est plus centré en ce point. Elle est placée de telle manière qu'elle présente une rotation de 30° autour de l'axe y passant par le sommet (-2.0,0.0,2.0) et que ce sommet soit sur sa surface. En outre, elle subit un zoom de rapport (0.5,1.0,1.0) par rapport à son centre.
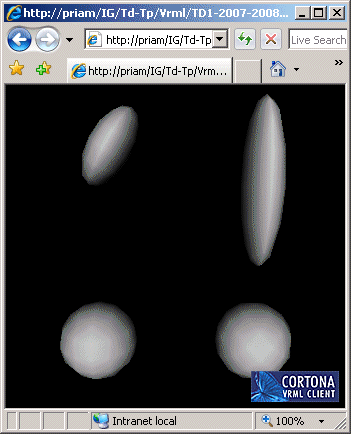
Solutions
![]()
TP n°1: Prise en mains d'un environnement de programmation VRML
Les viewers disponibles sont:
- Un plugin Internet Explorer/Netscape Navigator (Cortona Player)
- Une application de visualisation (Scene Viewer)
Travail demandé:
- Implantation des fichiers VRML du TD n°1.
- Implantation d'une scène avec un cube, une sphère, un cylindre et un cone pour vérifier le centrage et l'axe de dessin de ces objets.
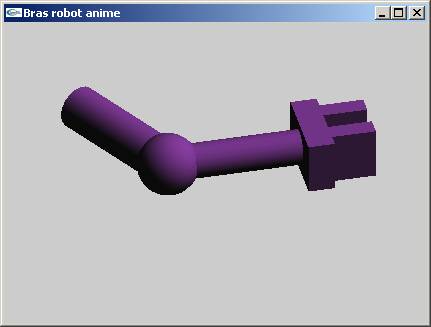
- Programmer la scène modélisant un bras robot composé d'un avant-bras, d'un bras, et
d'une paire de pinces.
L'avant-bras est articulé pour tourner autour de l'axe y d'un angle r1. Il s'agit d'un parallélépipède rectangle de dimension (3.0,1.0,1.0) (en rouge sur le shéma ci-dessous).
Le bras est articulé autour de l'axe y au bout de l'avant bras pour un angle r2. Il s'agit d'un parallélépipède rectangle de dimension (3.0,0.8,0.8) (en vert sur le shéma).
La pince est située au bout du bras. Elle peut tourner autour de l'axe du bras pour un angle r3. L'embase de la pince est un parallélépipède rectangle de dimension (0.6,1.2,1.8) (en bleu sur le shéma).
Chacune des mâchoires est un parallélépipède rectangle de dimension (1.0,1.2,0.4) (en jaune sur le shéma) à même de se déplacer longitudinalement d'une valeur d pour réaliser une ouverture totale de 2xd.
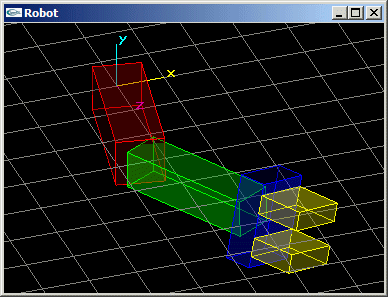
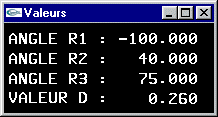
- Modification du bras robot pour que l'avant bras et le bras soient transformés en cylindres de diamètre 1.0 et 0.8 et de hauteur 3.0 et que l'articulation soit modélisée par un objet supplémentaire de type sphère de diamètre 1.4.
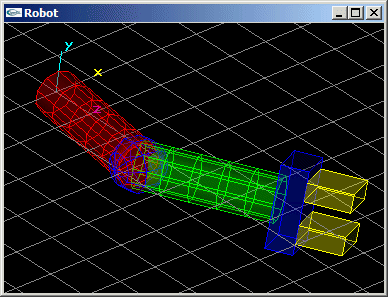
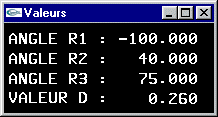
- Nouvelle modification du bras robot pour que les mandibules soient transformées en des cônes de rayon 0.2 et de hauteur 2.0 pointant vers l'intérieur de la pince avec un angle de r4 radians par rotation autour du centre de leurs bases.
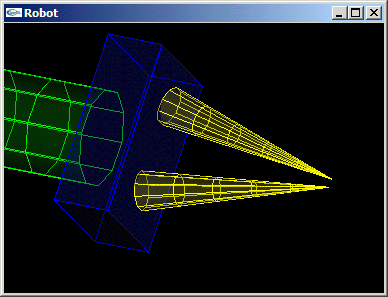
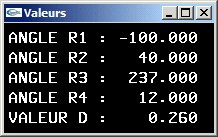
Solutions
| Scène (2) |
| Scène (3) |
| Test des objets |
| Le bras robot |
| Le bras robot avec cylindres |
| Le bras robot avec cylindres et cones |
![]()
TD n°2: Création de scènes OpenGL
Exercice n°1
Réaliser l'implantation OpenGL du bras robot du TP n°1.
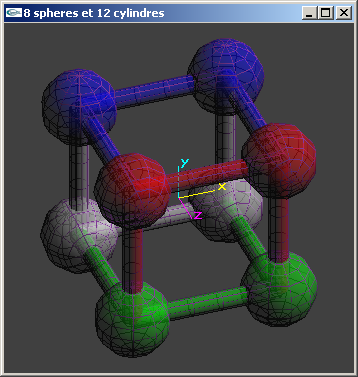
Exercice n°2
Soit la scène composée de huit sphères de rayon 1.0 centrées sur les
sommets d'un cube virtuel de coté 4 lui-même centré sur O, et de 12 cylindres de rayon
0.25 et de longueur 4.0 joignant ces 8 sommets entre eux pour matérialiser les arêtes du
cube de coté 4.
Implanter cette scène en une fonction C.

Fichiers sources pour dessiner des cylindres
ModuleCylindres.cpp
ModuleCylindres.h
Solutions
![]()
TP n°2: Prise en mains d'un environnement de programmation OpenGL
Création d'un projet Visual C++ permettant la compilation OpenGL
- Les fichiers d'inclusion (nécessaires à la compilation) spécifiques à OpenGL sont GL/gl.h et GL/glu.h ainsi que GL/glut.h si GLUT est utilisé.
- Les librairies d'édition de liens (nécessaires à la création de l'exécutable) spécifiques à OpenGL sont OpenGL32.lib et glu32.lib ainsi que glut32.lib si GLUT est utilisé.
- Les dll (nécessaires à l'exécution) spécifiques à OpenGL sont OpenGL32.dll et glu32.dll ainsi que glut32.dll si GLUT est utilisé.
Seul GLUT n'est pas installé lors de l'installation de Visual C++. Il est nécessaire de se procurer les fichiers .h, .lib et .dll lui correspondant puis de les installer.
Les librairies OpenGL32.lib et glu32.lib spécifient des fonctions situées dans OpenGL32.dll et glu32.dll spécifiques à la carte graphique installée.Suivant la manière avec laquelle Visual C++ à été installé, il pourra être nécessaire (ou non) de spécifier les fichiers .lib d'OpenGL dans les options de linkage.
Si gcc sous Linux est utilisé, Mesa3D devrait avoir été installé au cours de l'installation des outils de développement (gcc). S'il ne l'est pas, ou si l'on constate l'absence de GLUT, ou si l'on souhaite utiliser une version plus récente que celle disponible (en septembre 2007, la version la plus récente disponible de Mesa3D est la version 7.0.1 qui est compatible OpenGL 2.1), il sera nécessaire de télécharger et d'installer (compilation puis installation, une archive pour OpenGL, une archive pour GLUT et une archive pour des exemples) la version souhaitée.
Pour l'édition de lien d'un exécutable OpenGL & GLUT, il est nécessaire de spécifier les librairies GL, GLU et glut dans la ligne de commande de compilation.
Téléchargement du programme source exemple, compilation et exécution: AffichageInformationsRelease.cpp.
Exécutable compilé avec Visual C++ et l'OpenGL de Visual C++
Exécutable compilé avec Visual C++ et l'OpenGL Mesa3D
Téléchargement du programme source exemple destiné à être compilé et testé: Simple2007-2008.cpp.
Téléchargement du programme source exemple fonctionnel (définition d'une caméra, gestion du clavier, gestion correcte du fenêtrage, dessin d'une scène élairée ou non) destiné à être compilé et testé: OpenGL2007-2008.cpp.
Téléchargement du programme source exemple (animation) destiné à être testé: Animation2007-2008.cpp.

Dessin des objets de base GLUT pour repérer leurs caractéristiques de taille, d'orientation et de facettisation (en adaptant l'exemple OpenGL2007-2008.cpp).


Implantation des exercices du TD n°2 (en adaptant l'exemple OpenGL2007-2008.cpp).
Fichiers sources pour dessiner des cylindres
ModuleCylindres.cpp
ModuleCylindres.h


Solutions
![]()
TD n°3: Utilisation des contrôles clavier et souris sous GLUT
1) Implanter les contrôles clavier GLUT suivants permettant de faire bouger le bras robot des TD et TP n°2:
- touches 1 et 4 pour diminuer/augmenter l'angle r1,
- touches 2 et 5 pour diminuer/augmenter l'angle r2 dans les limites de l'intervalle [-120.0,120.0],
- touches 3 et 6 pour diminuer/augmenter l'angle r3,
- touches - et + pour diminuer/augmenter l'ouverture d dans les limites de l'intervalle [0.0,0.5],
- touches de curseur gauche et droite pour faire tourner le bras robot autour de l'axe Oy,
- touches de curseur haut et bas pour faire tourner le bras robot autour de l'axe Ox.
2) Implanter les contrôles souris permettant de faire tourner le bras robot au moyen de la souris par rotation autour des axes Oy et Ox en corrélation avec les déplacements de la souris en x et en y dans la fenêtre bouton gauche appuyé.

Solutions
![]()
TP n°3: Utilisation des contrôles clavier et souris sous GLUT
Fin du TP n°2 et implantation du TD n°3.
![]()
TD n°4: Les primitives graphiques en OpenGL
Exercice n°1
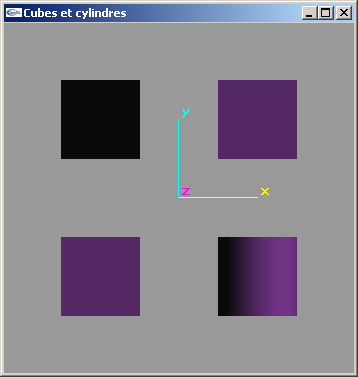
a) Ecrire une fonction de modélisation d'une boite cubique de coté c
centrée sur l'origine du repère.
Cette fonction devra seulement assurer la création des facettes (cubes blanc et noir
uniforme sur l'image ci-dessous).
b) Modifier la fonction précédente pour y inclure la spécification des normales aux facettes (utilisées par OpenGL pour les calculs d'éclairage) (cubes gris ombrés sur l'image ci-dessous).
Exercice n°2
a) Ecrire une fonction de modélisation d'un cylindre de rayon r, de
hauteur h, possédant n sections radiales, centré sur l'origine et d'axe y.
Cette fonction devra seulement assurer la création des facettes (cylindres gris uniformes
sur l'image ci-dessous).
b) Modifier la fonction précédente pour y inclure la spécification des normales aux facettes (utilisées par OpenGL pour les calculs d'éclairage) (cylindres avec ombrage gris sur l'image ci-dessous).
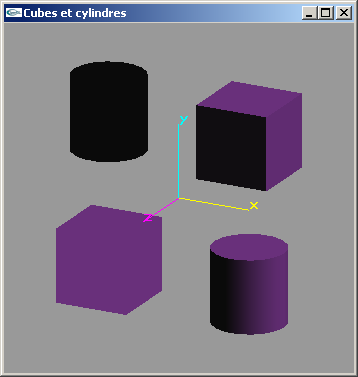
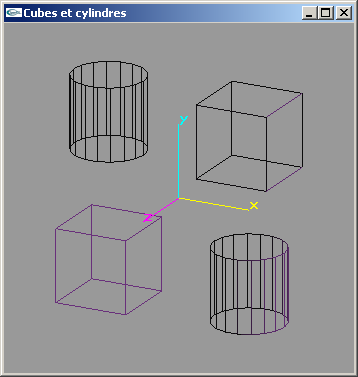
Solution
![]()
TP n°4: Gestion des caméras en OpenGL
Les programmes suivants implantent la gestion de caméras OpenGL selon différentes caractéristiques (différents types de caméras avec des paramétrages différents). Ils serviront de base de travail pour l'exercice de TP.
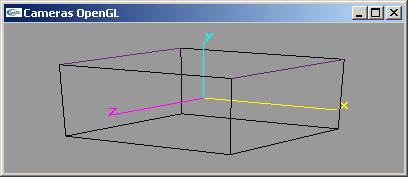
- CameraOpenGL01.cpp
Placement intégral dans la fonction display du code lié à la gestion de la caméra.
Pas de gestion correcte du ratio largeur/hauteur de la fenêtre.
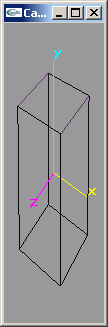 |
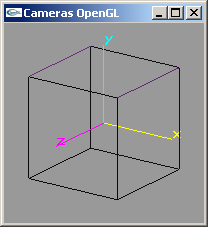 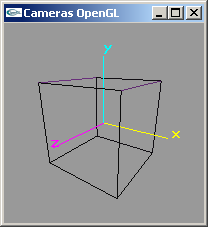 |
 |
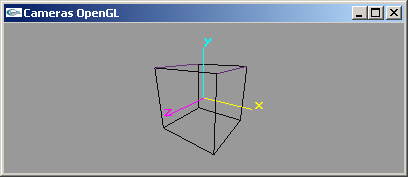
- CameraOpenGL02.cpp
Placement intégral dans la fonction display du code lié à la gestion de la caméra.
Gestion correcte du ratio largeur/hauteur de la fenêtre mais utilisation de code GLUT pour calculer la taille de la fenêtre.
|
 |
 |
- CameraOpenGL03.cpp
Gestion correcte du ratio largeur/hauteur de la fenêtre.
Répartition du code lié à la caméra entre les fonctions display (dessin d'une image en mode modelview) et reshape (configuration du mode projection).
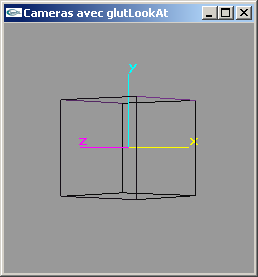
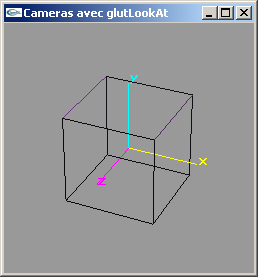
Plus de code GLUT dans le code gl mais appel directe à reshape depuis keyboard. - CameraOpenGLGluLookAt.cpp
"Production" d'un point de vue particulier par utilisation de la fonction gluLookAt (en mode modelview) entre la fin de la définition du mode projection et le dessin de la scène.

Exercice n°1
Le fichier DeplacementCameraScene.cpp (décrit par le fichier d'entête DeplacementCameraScene.h) contient une fonction void scene(int l) de modélisation d'une scène composée d'une surface plane carrée de diagonale (-10.0, 0.0, -10.0) - (10.0, 0.0, 10.0) sur laquelle sont posés aléatoirement 100 "poteaux" parallélipipédiques. L'éclairage de cette scène est activé/désactivé par le paramètre booléen l.

Implanter le dessin de cette scène par une caméra de visualisation en perspective placée en position (0.0, 0.5, 0.0) orientée dans la direction (0.0, 0.0, 1.0). L'ouverture verticale de la caméra est de 60°. Les plans cmin est cmax sont aux distances 0.1 et 100.0. La taille de la fenêtre d'affichage est 450 sur 200 pixels.
Exercice n°2
Modifier le programme précédent pour autoriser le déplacement de la caméra au moyen des touches up et down de manière à avancer et reculer dans la scène dans l'axe de la caméra.
Exercice n°3
Modifier le programme précédent pour autoriser l'utilisation des touches right et left de manière à faire tourner la caméra vers la droite et vers la gauche tout en continuant à pourvoir utiliser les touches up et down pour avancer et reculer.
Solution
![]()
TD n°5: Animation automatique en OpenGL et GLUT
Exercice n°1
On considère une scène quelconque modélisée au sein de la fonction void
scene(void).
On considère la fonction display suivante d'un programme OpenGL + GLUT dessinant cette
scene:
void display(void) {
glClearColor(0.6F,0.6F,0.6F,1.0F) ;
glClear(GL_COLOR_BUFFER_BIT|GL_DEPTH_BUFFER_BIT) ;
glPushMatrix();
scene();
glPopMatrix();
glFlush();
glutSwapBuffers();
}
Modifier cette fonction display et écrire la fonction idle réalisant l'animation automatique de la scène par rotation sur elle-même autour de l'axe Ox à raison de 1° de rotation entre chaque image.
Implanter un contrôle clavier utilisant la touche espace pour activer/désactiver cette animation.

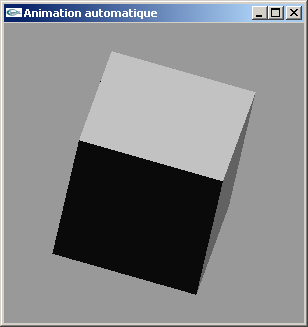


Exercice n°2
Modifier la fonction display de l'exercice n°1 pour implanter une animation de caméra de telle manière que celle-ci se déplace sur une trajectoire circulaire d'"altitude" constante y = 7.0, de rayon 20.0 et de centre (0.0, 7.0, 0.0) à raison de 0.1° de rotation entre chaque image. La caméra est orientée en direction du point de coordonnées (0.0, 1.0, 0.0)
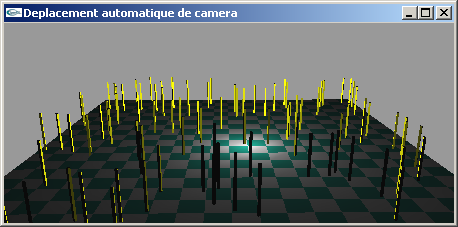
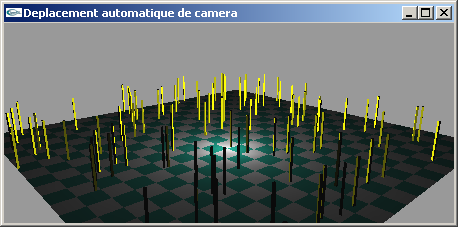
Exercice n°3
On souhaite implanter un système de particules modélisant un des objets en rotation autour d'un point d'attraction gravitationnelle. La formule définissant la période de révolution T d'un objet en orbite circulaire autour d'un autre objet (2ème loi de Kepler) est T = C*r1.5. r est le rayon de l'orbite. C est une constante qui dépend de la constante d'attraction universelle et de la masse centrale dans le cas d'une orbite circulaire. On utilisera C en tant que variable d'ajustement de la vitesse de rotation.
a) Développer un programme OpenGL permettant d'animer une seule particule sphèrique
de rayon 1.0 par rotation autour de O dans le plan xOy selon une trajectoire orbitale
circulaire de rayon r avec une vitesse calculée en accord avec la loi de Kepler (définie
ci-dessus).
Le rayon r pourra être contrôlé via les touches + et - du clavier pour varier entre les
bornes 1.5 et 10.0.


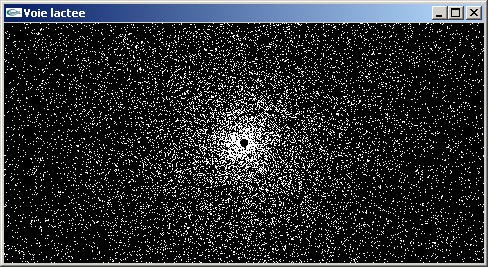
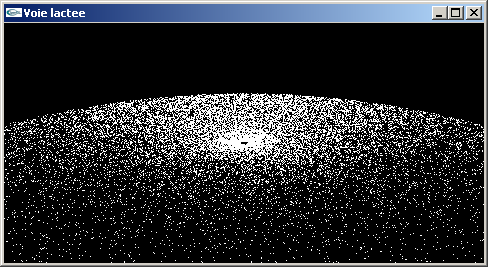
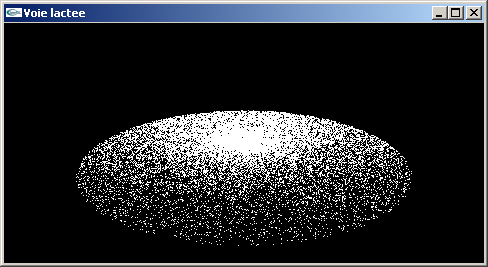
b) Modifier le programme précédent pour animer 25000 particules au lieu d'une seule.
Chacune d'elles sera modélisée par un pixel au lieu d'une sphère. Elles seront
réparties aléatoirement de r = 0.1 à r = 10.0. Elles seront aussi réparties
aléatoirement sur leurs orbites.

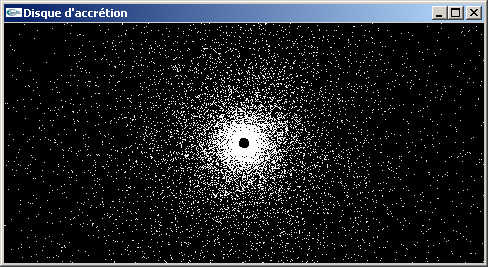
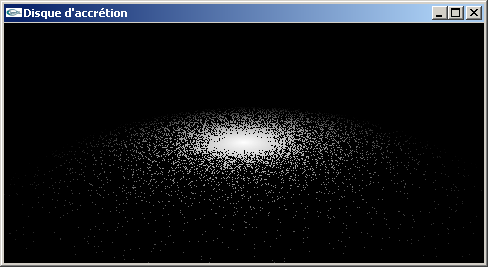
c) On souhaite maintenant implanter une décroissance au cours du temps du rayon de
l'orbite des particules de manière que cette décroissance soit réalisée selon la
formule récurrente suivante ri+1 = 0.99*ri où i est le numéro
l'image.
Les particules sont créées à raison de 20 nouvelles particules à chaque nouvelle image
pour une durée de vie de 1100 images soit donc au total 22000 particules. Elles sont
créées à une distance r = 40.0 aléatoirement sur leurs orbites. Toute particule qui
disparait est remplacée par une nouvelle particule. Les couleurs des particules varient
du noir au blanc linéairement en fonction de leurs distances au centre.


Solutions
![]()
TP n°5: Matériaux et lumières en VRML
Dans les exercices suivants, on s'attachera à tester les diverses options de rendu relatives à la gestion des ombrages proposée par le viewer VRML utilisé.
Exercice n°1
a) Ecrire une scène VRML composée d'une sphère possédant les
caractéristiques suivantes:
- rayon: 5.0,
- centrée sur l'origine du repère,
- affectée d'un matériel avec uniquement de la diffusion dans le rouge.
Tester l'activation/désactivation de la lampe frontale.
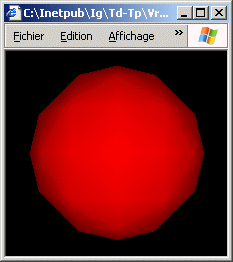
b) Modifier la scène précédente pour que le matériel intègre une composante de réflexion spéculaire dans le vert. Tester différentes réflectivités.
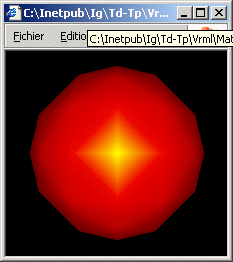
c) Modifier la scène précédente pour y intégrer un éclairage sous la forme d'une source lumineuse directionnelle blanche éclairant depuis la droite. Désactiver la lampe frontale.

d) Modifier la scène précédente pour y inclure une seconde sphère de rayon 2 placée en position (10.0, 0.0, 0.0) possédant le même matériel que la première ainsi qu'une seconde source lumineuse ponctuelle blanche placée à l'origine.
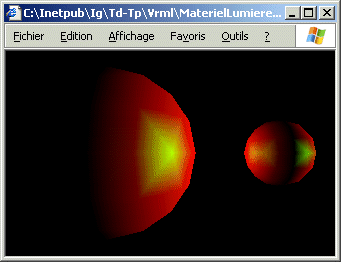
e) Modifier la scène précédente pour y inclure une source lumineuse
spot blanche placée en position (0.0, 0.0, 10.0) orientée vers l'origine et éclairant
partiellement la grosse sphère.
Tester les différentes préférences de votre viewer VRML.

Solutions
VRML |
||||||
| Les fichiers VRML | ||||||
Exercice n°2
On considère le matériel suivant:
Material {diffuseColor 0 1 0
specularColor 0 0 1
shininess 0.25
ambientColor 1 0 0
emissiveColor 0.2 0.2 0.2
transparency 0
}
Analyser les contributions respectives des différentes caractéristiques de ce matériel en l'utilisant dans le cadre de l'exercice n°1.
Solution
VRML |
||||||
| Les fichiers VRML | ||||||
Exercice 3
On souhaite vérifier le fonctionnement de la gestion des transparences
dans les matériaux vrml.
Implanter une scène composée de 2 sphères munies d'un matériel 1/2 transparent. Par
rotation de cette scène sur elle-même vérifier le comportement de votre viewer.
![]()
TD n°6: Calcul mathématique de la diffusion au moyen de la formule de Lambert
Le travail est à réaliser en langage java.
Exercice n°1
a) Définir une classe position dans un espace à 3 dimensions
b) Définir une classe direction dans un espace à 3 dimensions
c) Définir une classe couleur RVB.
d) Définir une classe destinée à modéliser un matériel générant des réflexions diffuses.
e) Définir une classe destinée à modéliser une lumière directionnelle
f) Définir une classe énergie RVB.
g) Implanter une méthode de calcul de l'énergie colorée diffusée au niveau d'un point d'une surface munie d'un matériel sous l'éclairage d'une lumière directionnelle. La normale au point vis à vis de la surface est connue.
Exercice n°2
a) Définir une classe destinée à modéliser une lumière ponctuelle
b) Implanter une méthode de calcul de l'énergie colorée diffusée au niveau d'un point d'une surface munie d'un matériel sous l'éclairage d'une lumière ponctuelle. La normale au point vis à vis de la surface est connue.
![]()
TP n°6: Matériaux et lumières en OpenGL
- Implanter en OpenGL la scène finale de l'exercice n°1 du TP n°5.

- Animer la source lumineuse ponctuelle pour qu'elle réalise un mouvement de va et vient vertical entre les positions (0.0, 10.0, 0.0) et (0.0, -10.0, 0.0).
- Animer le spot pour qu'il tourne autour de lui-même dans le plan xOz.

- Implanter en OpenGL l'exercice n°2 du TP n°5.
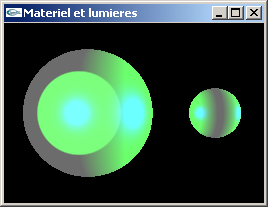
Image avec tous les types de lumière en synthèse additive


Composantes diffuse et spéculaire


Composantes ambiante et émise
Solutions
![]()
TD n°7: Mathématiques pour l'Informatique Graphique
Ce TD reprend et complète le TD n°6.
a) Développer une méthode de calcul du produit vectoriel de deux objets Direction.
b) Ecrire une méthode de calcul de la norme d'une Direction.
c) Ecrire une méthode normalisation d'une Direction.
d) Ecrire un constructeur de la classe Direction pour calculer la direction normée définie par deux objets Position.
e) Définir une classe facette à 4 sommets.
f) Ecrire une méthode de test de la planarité d'une facette à 4 sommets.
g) Ecrire une méthode de test de la convexité du bord d'une facette considérée comme plane.
h) Définir une classe de définition géométrique d'un rayon lumineux issu d'une source ponctuelle.
g) Définir une classe sphère.
i) Ecrire une méthode de test de l'intersection entre un rayon lumineux et une sphère.
j) Ecrire une méthode de calcul de (ou des) intersection(s) entre un rayon lumineux et une sphère.
![]()
TP n°7: Mathématiques matricielles
TP à réaliser en Java.
a) Définir une classe transformation géométrique en coordonnées homogènes 3D.
b) Dériver de cette classe une identite.
c) Dériver une classe translation de la classe de la question (a).
d) Dériver une classe rotation de la classe de la question (a).
e) Dériver une classe scale de la classe de la question (a).
f) Définir une classe coordonnées homogènes 3D.
g) Dériver de cette classe une classe Position.
h) Dériver une classe Direction de la classe de la question (e).
i) Implanter le produit matrice.vecteur pour la réalisation de transformations géométriques sur des coordonnées homogènes 3D.
j) Implanter le produit matrice.matrice pour la composition de transformations géométriques 3D.
![]()
TD n°8: Introduction au plaçage de texture
![]()
TP n°8: Plaçage de texture
Exercice n°1: Le texturage en VRML
Le fichier VRML Sphere.wrl implante l'affichage d'une sphère non texturée. Modifier ce fichier pour texturer la sphère au moyen de l'image Terre-02048.png en utilisant le noeud propriété Texture2.

Exercice n°2: Le texturage en OpenGL
Le but de cet exercice est d'obtenir le même résultat que l'exercice n°1 dans le
cadre de la programmation d'une application C + OpenGL en Visual C++.
Le fichier image à utiliser est toujours le même: Terre-02048.png. Il s'agit d'un fichier
au format png contenant une image de 2048 par 1024 pixels.
L'importation d'une image png pourra être réalisé au moyen de la fonction unsigned char *chargeImagePng(char *,int *,int *)
décrite dans le fichier d'entête ChargePngFile.h.
Le résultat de cette fonction est un tableau d'"unsigned char" alloué au sein
de la fonction et rempli avec les composantes r, v, b de chaque pixel de l'image lue. Si
la lecture n'a pas pu être effectuée, la fonction rend NULL. Le premier paramètre
d'entête est la chaine de caractères contenant le nom du fichier png à importer. Le
deuxième paramètre est un pointeur sur int destiné à retourner la résolution rx en x
de l'image lue. Le troisième paramètre est un pointeur sur int destiné à retourner la
résolution ry en y de l'image lue. -> Le tableau rendu contiendra 3 * rx * ry octets.
Les deux fichiers librairies statiques Visual C++ Libpng.lib et LibChargePngFile.lib contiennent
l'implantation de cette fonction et de toutes les fonctions utilisées par cette fonction.
Il sont donc nécessaires à la phase d'édition de liens lors de la création de
l'exécutable et devront être inclus dans le projet.
ATTENTION, la génération d'une cible en configuration "Debug" n'est pas possible au moyen de ces librairies. La compilation en configuration "Release" est nécessaire.
ATTENTION, l'exclusion de la librairie libc.lib pourrait être nécessaire lors de l'édition de lien de manière à éviter la duplication de certaines fonctions entre librairies par défaut.

Le fichier SphereTexturee.cpp contient un programme C + OpenGL qui utilise la fonction chargeImagePng pour importer une image dans un tableau puis utilise ce tableau (de pixels) en tant que texture. Le code correspondant à ces opérations est à la fin de la fonction init.
Une fois le plaçage de texture activé via l'exécution de
glEnable(GL_TEXTURE_2D) tout objet dessiné le sera avec texturage.
Notre but est de dessiner une sphère texturée. Or, la fonction de modélisation de
sphère de GLUT n'assure pas la génération des coordonnées de texturage et ne peut donc
pas être utilisée.
Avec utilisation de glutSolidSphere
a) Développer le fichier ModuleSphere.cpp contenant une fonction nommée mySolidSphere possédant un prototype identique à celui de glutSolidSphere. Cette fonction réalisera le dessin d'une sphère et assurera la génération des coordonnées de texturage de cette sphère.
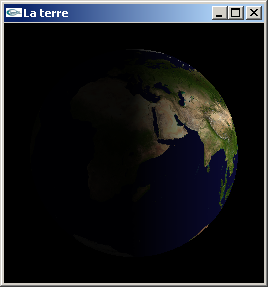
On pourra utiliser la fonction suivante:
#ifndef M_PI
#define M_PI 3.14159
#endif
void mySolidSphere(float rayon,int nlat,int nlon) {
for ( int i = 0 ; i < nlat ; i++ ) {
float a1 = -M_PI/2.0F + i*M_PI/nlat ;
float a2 = a1 + M_PI/nlat ;
float cs1 = cos(a1);
float cs2 = cos(a2);
float sn1 = sin(a1);
float sn2 = sin(a2);
glBegin(GL_QUAD_STRIP);
for ( int j = 0 ; j <= nlon ; j++ ) {
float a = j*2*M_PI/nlon;
float x1 = cs1*cos(a);
float z1 = cs1*sin(a);
float x2 = cs2*cos(a);
float z2 = cs2*sin(a);
glNormal3f(x1,sn1,z1);
glVertex3f(rayon*x1,rayon*sn1,rayon*z1);
glNormal3f(x2,sn2,z2);
glVertex3f(rayon*x2,rayon*sn2,rayon*z2); }
glEnd(); }
}
en lui ajoutant le code nécessaire à la génération des coordonnées de texturage (code
qu'elle n'inclut pas). Cette fonction est implantée dans le fichier ModuleSpheres2.cpp avec comme fichier
d'entête ModuleSpheres.h.
Solution
![]()
TD n°9: Clipping par l'algorithme de Cohen-Sutherland
L'implantation est réalisée en langage java.
a) Définir trois classes de stockage pour:
- des positions en deux dimensions,
- des segments de droites 2D,
- des rectangles 2D à cotés verticaux et horizontaux.
b) Implanter une méthode permettant de calculer le code de Cohen-Sutherland associé à une position vis à vis d'un rectangle.
c) Implanter une méthode permettant de calculer l'abscisse de l'intersection d'une droite horizontale avec la droite supportée par un segment.
d) Implanter une méthode permettant de calculer l'ordonnée de l'intersection d'une droite verticale avec la droite supportée par un segment.
e) Implanter une méthode de calcul du segment clippé d'un segment vis à vis d'un rectangle.
![]()
TP n°9: L'algorithme de Bresenham pour le tracé de segments 3D et le remplissage d'une facette triangulaire 2D
Le programme Bresenham.cpp utilise la version de l'algorithme de Bresenham dédié au dessin d'un segment sur une écran bitmap.
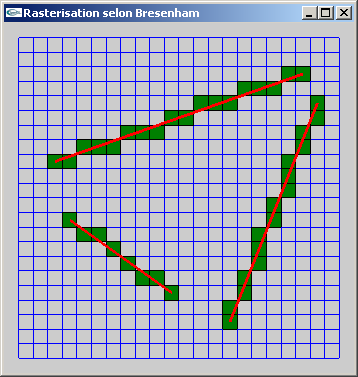
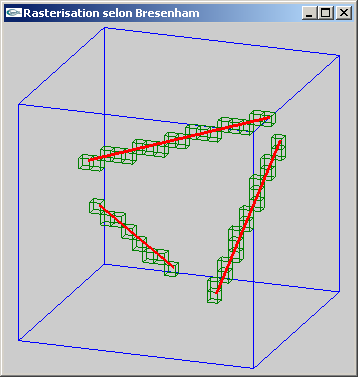 a
a
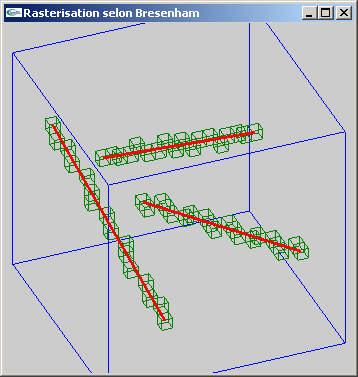
a) Généraliser cet algorithme 2D au dessin de segments 3D.
b) Utiliser cet algorithme pour développer un algorithme de remplissage des facette triangulaire 2D.
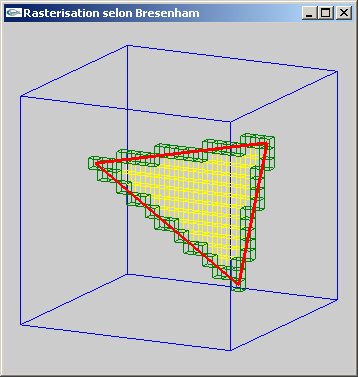
Solutions
![]()
TD n°10: Calcul de l'intersection entre une sphère et un rayon, des rayons réfléchi et transmis dans le cadre de l'implantation d'un algorithme de lancer de rayons
Le TD est réalisé en langage C. Les structures suivantes devront être utilisées:
- typedef struct position {
double x;
double y;
double z;
double t; } position; - typedef struct direction {
double x;
double y;
double z;
double t; } direction; - typedef struct sphere {
position centre;
double rayon; } sphere; - typedef struct rayonLumineux {
position origine;
direction direction; } rayonLumineux;
a) Implanter une fonction permettant de tester l'existence d'une intersection entre un rayon lumineux et une sphère.
b) Implanter une fonction permettant de déterminer, si elle existe, la distance entre le point d'émission d'un rayon lumineux et l'intersection entre ce rayon et une sphère.
c) Implanter une fonction permettant de calculer la direction du rayon réfléchi créé par un rayon incident à l'interface entre deux milieux.
d) Implanter une fonction permettant de calculer la direction du rayon transmis créé par un rayon incident à l'interface entre deux milieux.
![]()
TP n°10: Calcul de l'intersection entre une sphère et un rayon, des rayons réfléchi et transmis dans le cadre de l'implantation d'un algorithme de lancer de rayons
a) Implanter les 4 questions du TD n°10 sous la forme de fonctions respectant les prototypes suivants:
- int intersection(rayonLumineux *rl, sphere *sp);
- int intersection(rayonLumineux *rl, sphere *sp, double *d);
- void reflexion(direction *r, direction *i, direction *n);
- int transmission(direction *t, direction *i, direction *n, double niSurnt);
b) Implanter les 4 fonctions de la question a) dans le programme MiniRayTracingIncomplet.cpp qui les utilise dans le cadre d'un algorithme de lancer de rayons pour le dessin de scènes constituées de sphères éclairées par des sources lumineuses ponctuelles ou directionnelles.
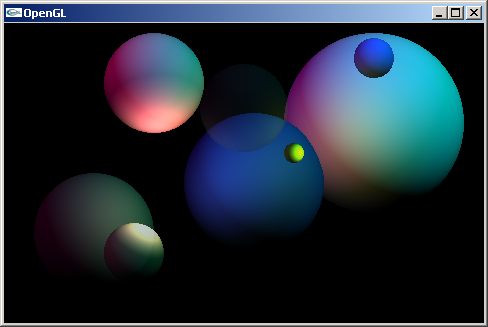
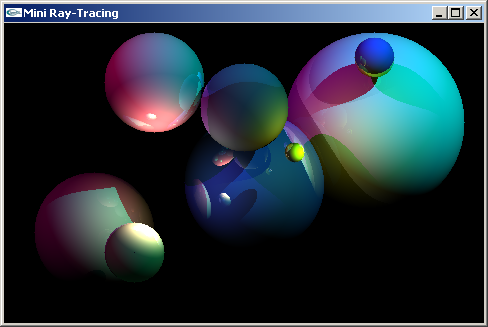
La même scène affichée avec l'algorithme de rendu intégré
à notre OpenGL et avec un algorithme de lancer de rayons
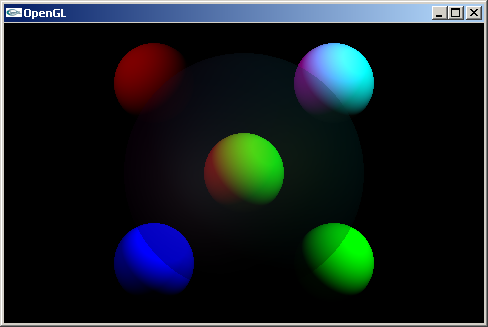
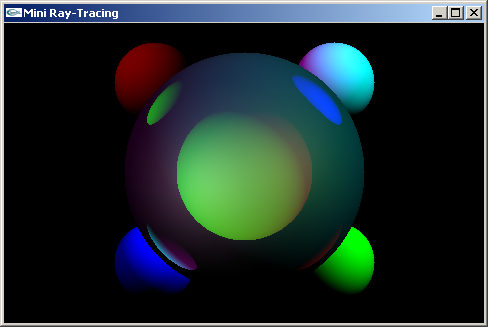
La même scène affichée avec l'algorithme de rendu intégré
à notre OpenGL et avec un algorithme de lancer de rayons
Solution
![]()
Le TD est réalisé en langage C.
Les structures suivantes devront être utilisées:
- typedef struct position {
double x;
double y;
double z;
double t; } position; - typedef double matriceBase[4][4];
Ainsi que les matrices de base suivantes:
- static matriceDeBase mBNRU =
{ { -0.16667F, 0.5F, -0.5F, 0.16667F },
{ 0.5F , -1.0F, 0.5F, 0.0F },
{ -0.5F , 0.0F, 0.5F, 0.0F },
{ 0.16667F, 0.66667F, 0.16667F,0.0F } }; - static matriceDeBase mBCR =
{ { -0.5F, 1.5F,-1.5F, 0.5F },
{ 1.0F,-2.5F, 2.0F,-0.5F },
{ -0.5F, 0.0F, 0.5F, 0.0F },
{ 0.0F, 1.0F, 0.0F, 0.0F } }; - static matriceDeBase mBB =
{ { -1.0F, 3.0F,-3.0F, 1.0F },
{ 3.0F,-6.0F, 3.0F, 0.0F },
{ -3.0F, 3.0F, 0.0F, 0.0F },
{ 1.0F, 0.0F, 0.0F, 0.0F } };
Implanter une fonction de dessin d'une courbe B-Spline définie sur 4 points de contrôle.
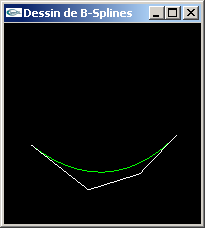
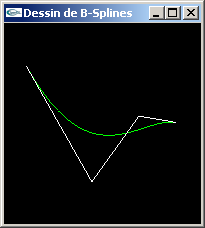
B-Splines de Bezier
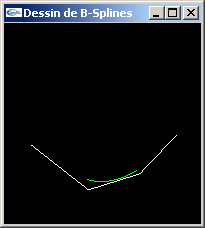
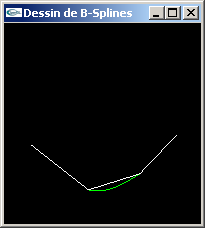
B-Splines non rationnelles uniformes et de Catmull-Rom
![]()
TP n°11: Implantation du dessin de courbes B-Spline
a) Implanter le TP n°11.
b) Utiliser la fonction de la question a) pour implanter le dessin d'une courbe B-Spline par morceaux définie sur n points de contrôle (n >= 4).
On pourra utiliser la structure suivante pour implanter une ligne polygonale:
- typedef struct lignePolygonale {
int n;
position *pts; } lignePolygonale;
On pourra aussi utiliser la ligne polygonale suivante:
- static position p1[10] =
{ { -6.0,-1.0, 5.0, 1.0 },
{ -1.0,-6.0,-4.0, 1.0 },
{ 3.0,-4.0, 1.0, 1.0 },
{ 6.0,-1.0, 0.0, 1.0 },
{ 5.0, 3.0,-2.0, 1.0 },
{ 1.0, 6.0, 4.0, 1.0 },
{ -1.0, 2.0, 1.0, 1.0 },
{ -4.0, 2.0, 2.0, 1.0 },
{ -5.0, 6.0,-3.0, 1.0 },
{ -2.0, 5.0,-6.0, 1.0 } }; - static lignePolygonale lp = { 10,p1 };
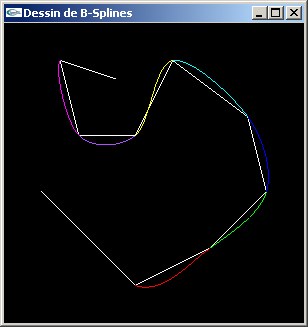
B-Splines de Catmull-Rom:
La méthode fonctionne.
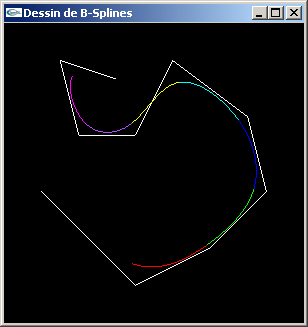
B-Splines non rationnelles uniformes:
La méthode fonctionne.
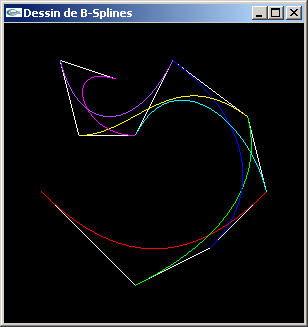
B-Splines de Bézier:
La méthode ne fonctionne pas.
Solution
![]()
